ATMO/ECE 489/589 Spring 2017
Homework #2 Answers
1a. A charge +Q is positioned a
distance H above a grounded conducting plane (the earth's
surface).


Negative charge appears on the surface of the conductor so that no field is present inside the conductor (field lines radiating outward from Q terminate on negative charges on the ground). The highest concentration of charge is directly below the charge Q. Q is attracted to the negative charge at the surface of the ground. Sorry about using both Q and q in what follows. It would have been too much work to go back and replace q with Q in all the figures.
1b. In order to determine the electric field at the surface, we make use of the method of images and replace the ground with an image charge, -Q, a distance H below the ground. The original charge and its image mean the potential at z = 0 is zero, the same as with a single charge Q sitting above a grounded conducting plane. Then we can determine the electric field that the two charges would produce at z = 0.
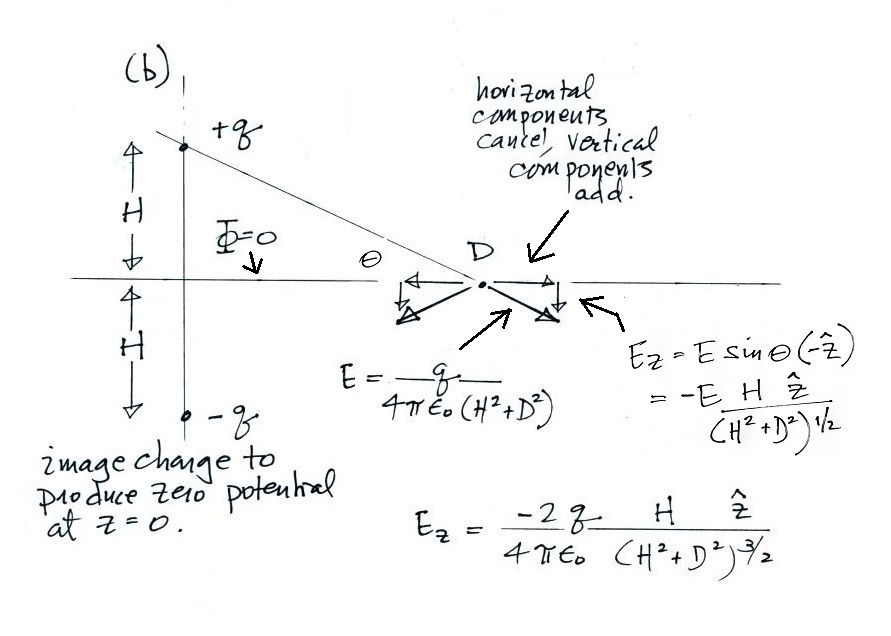
The horizontal components of E cancel
(something that would be true at the surface of a
conductor). The two perpendicular components
add. Ez as a function of D is shown above.
1c. Next we make use of the relation between E field and the surface charge density found at the surface of a conductor.
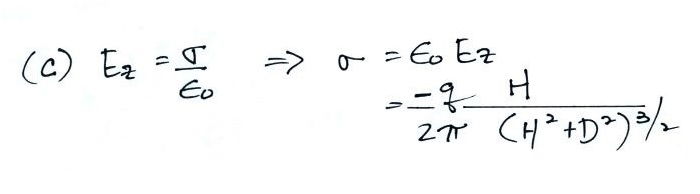
1c. Next we make use of the relation between E field and the surface charge density found at the surface of a conductor.
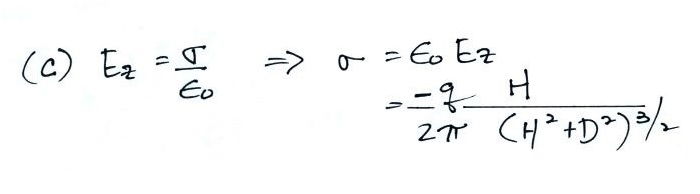
1d. Since the surface
charge density varies with D we determine the charge
is a ring, dQ, by multiplyingthe surface charge
density, σ,
by the area of the ring, 2 π D dD.
We end up with -q,


2.
In this problem we have a 500 m thick layer
of positive charge. We assume the layer is
of infinite horizontal extent and that charge is
distributed uniformly throughout the layer.
The volume space charge density, ρ, is 1 nC/m3
.
We'd expect to find a vertical E field pointing away from a layer of positive charge. The E will point upward above the top surface of the layer and downward from the bottom side of the layer. This is shown below.
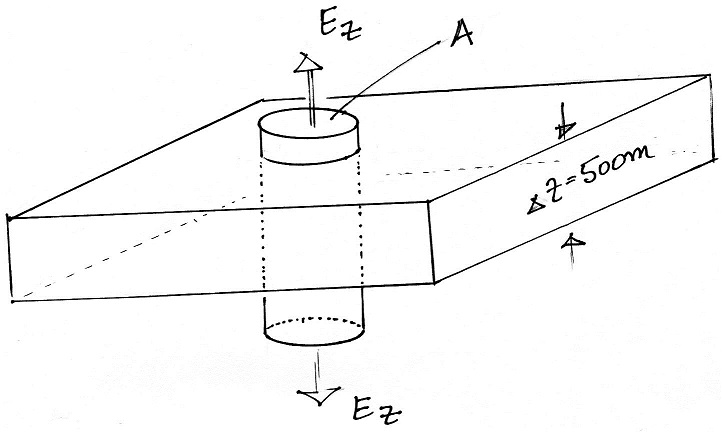
We'd expect to find a vertical E field pointing away from a layer of positive charge. The E will point upward above the top surface of the layer and downward from the bottom side of the layer. This is shown below.

We'll use the integral form
of Gauss' law and the cylindrical surface
shown above. We won't get any
contribution to the surface integral from the
sides of the cylinder because E is parallel to
the sides and perpendicular to the normal
vector; the dot product of E and the normal
vector is zero. E and the normal vector
are parallell at the two ends of the cylinder.
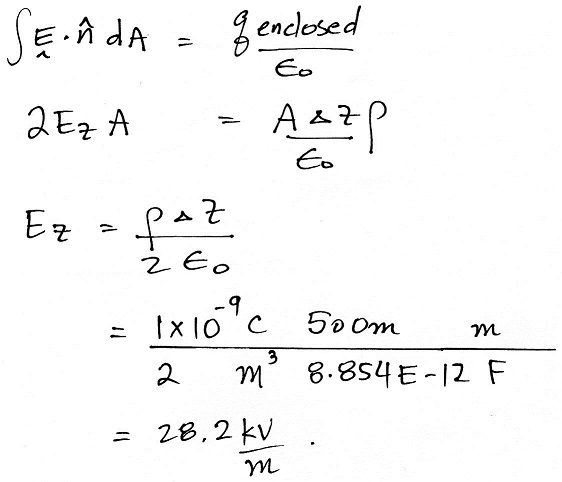
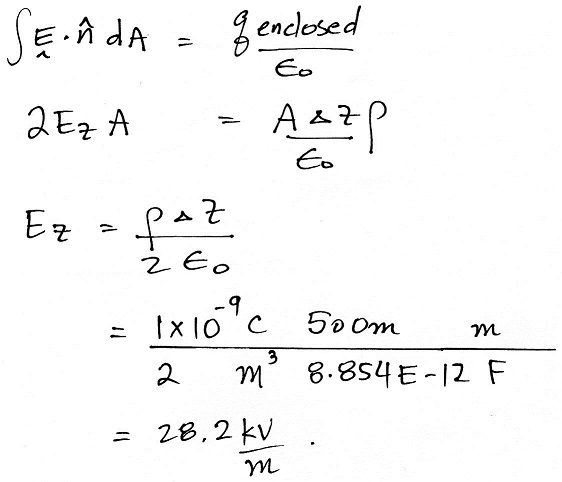
Ez is +28.2 kV/m above
the layer and -28.2 kV/m below the
layer. With an infinite layer the E
field will remain constant as you move
upward or downward away from the layer.
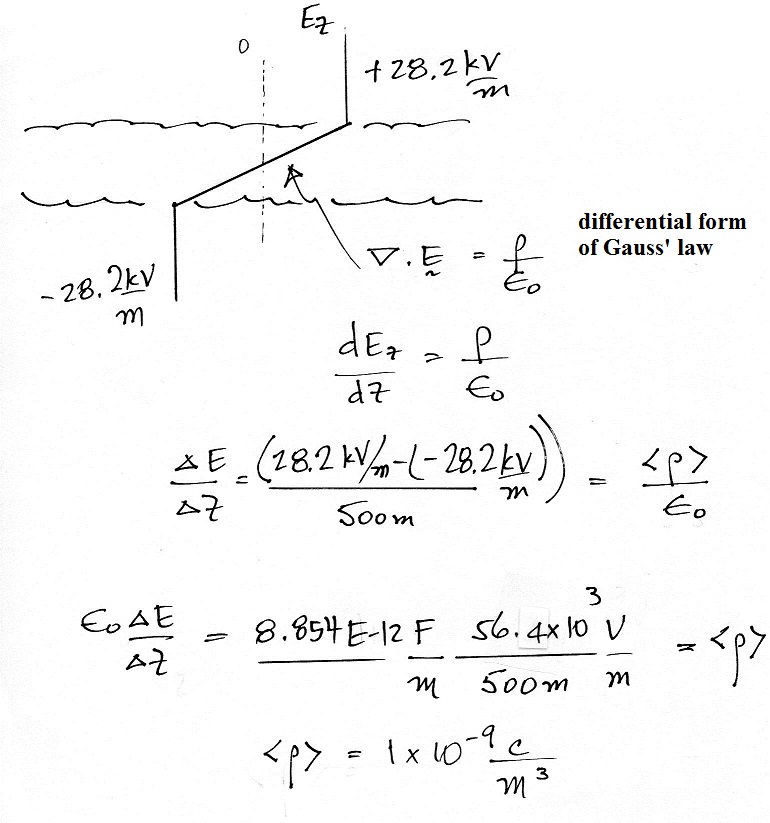

As we move through
the layer the E field should change
linearly from its -28.3 kV/m value to
its +28.2 kV/m above the layer.
We can use the rate of change of E,
dE/dz, and Gauss law to compute the
average volume space charge density
and see if it agrees with the value
given in the problem. We see
above that is the case.
2. In this question we are supposed to find the potential difference between the ground and 30 km altitude. We're given two equations for the electric field, Ez, as a function of altitude. One is applicable between 0 and 10 km, the other between 10 and 30 km.
You need to be careful with + and - signs and also with the 2.8 km and 8.3 km arguments in the exponents. You might need to convert the latter two to meters in some places.
Here's the first, 0 to 10 km, part of the problem
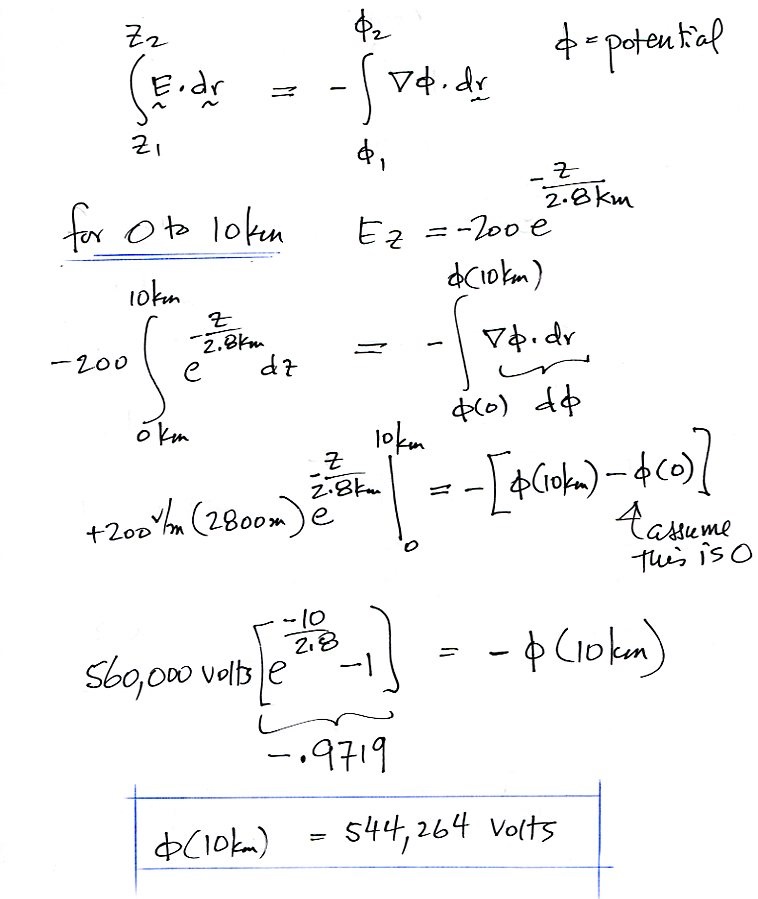
2. In this question we are supposed to find the potential difference between the ground and 30 km altitude. We're given two equations for the electric field, Ez, as a function of altitude. One is applicable between 0 and 10 km, the other between 10 and 30 km.
You need to be careful with + and - signs and also with the 2.8 km and 8.3 km arguments in the exponents. You might need to convert the latter two to meters in some places.
Here's the first, 0 to 10 km, part of the problem

and now the 10
to 30 km portion. E field is
weaker, so this won't contribute
as much to the total potential
difference.

We'll use cartesian coordinates. Potential is a function of just z.

We use the two boundary conditions (φ = 0 at z = 0 and φ = V at z = d) to determine the values of the constants A and b.
The potential gradient points upward in the direction of increasing potential. The electric field is - grad( potential gradient) and points downward. The electric field is constant (no variation with z) in the region between the plates.

The result
is somewhat larger than the
300,000 volt potential
differential used on the first
day of class.
4.
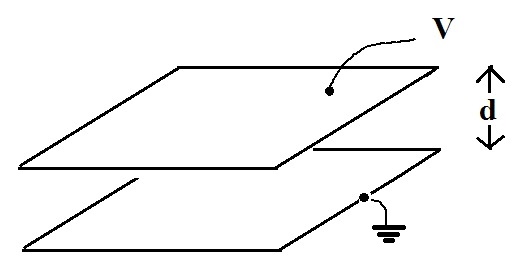
We're going to solve Laplaces equation to determine the potential and the electric field in the region between the two parallel plates shown above.

4.

We're going to solve Laplaces equation to determine the potential and the electric field in the region between the two parallel plates shown above.

We'll use cartesian coordinates. Potential is a function of just z.

We use the two boundary conditions (φ = 0 at z = 0 and φ = V at z = d) to determine the values of the constants A and b.
The potential gradient points upward in the direction of increasing potential. The electric field is - grad( potential gradient) and points downward. The electric field is constant (no variation with z) in the region between the plates.