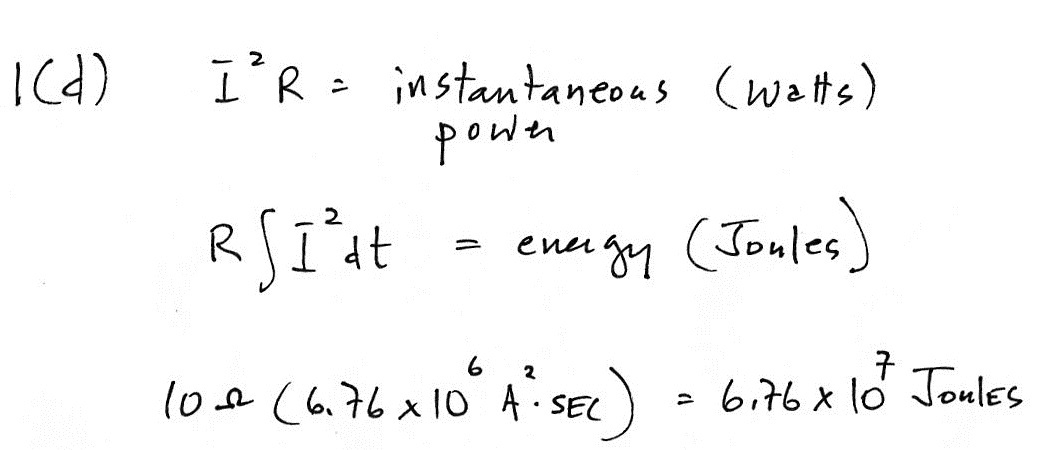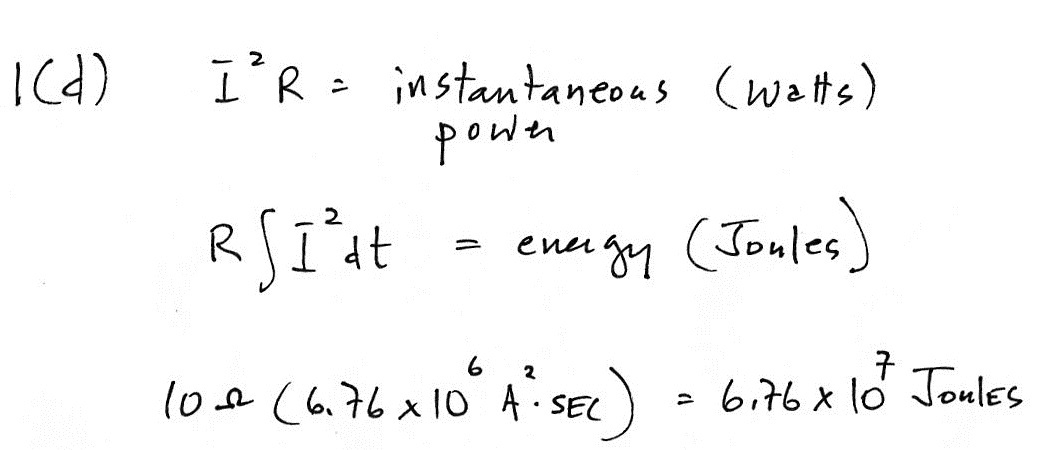ATMO/ECE 489/589  Spring 2017 Homework #5 Answers

#1a
Determining the peak value of dI/dt was fairly quick


#1b
In this part of the problem we needed to determine the charge transfer for each of the three intervals. 
This involved finding the area under the curve (current x time = charge).



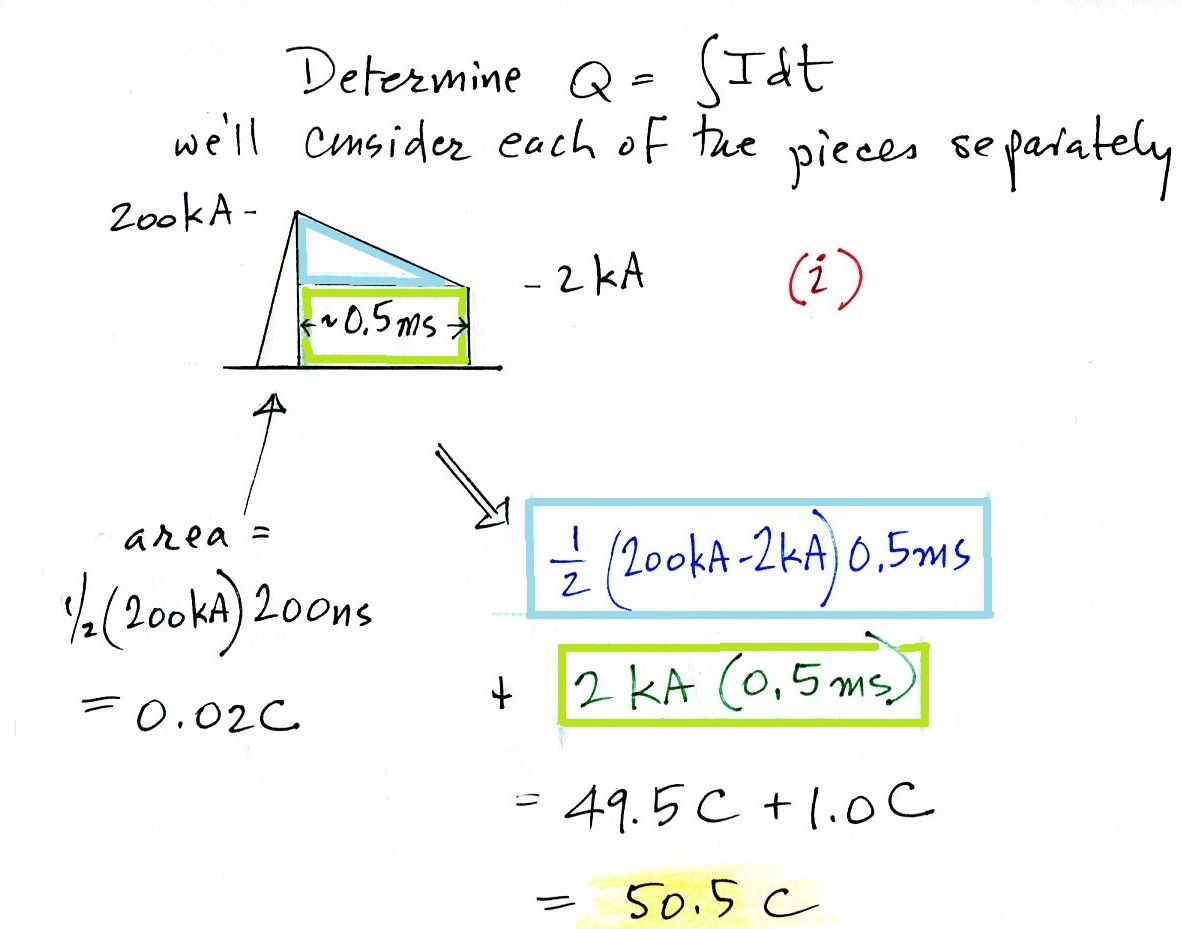
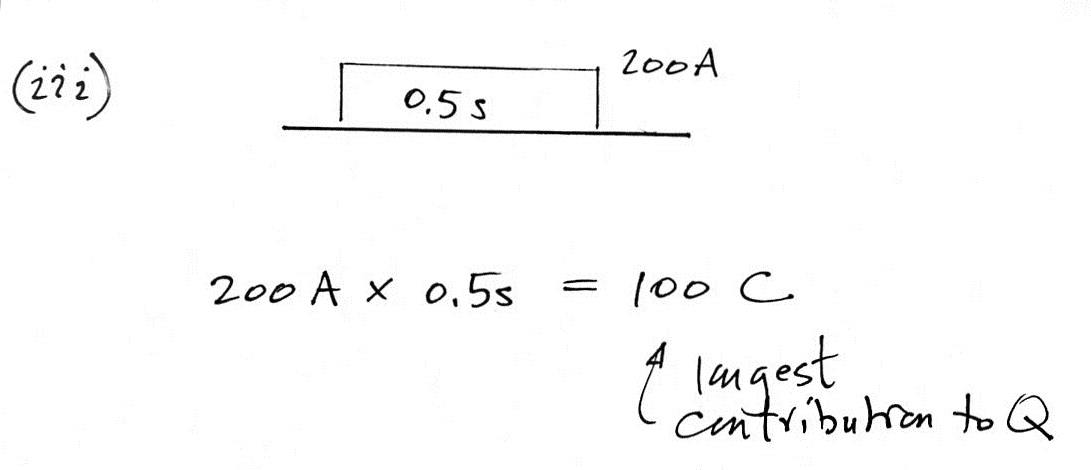
Here's the charge in (i).  The amount of charge in the 200 ns rise to peak current was so small that it was ignored.  The width of the second portion of this part of the waveform is actually 0.5 ms - 200 ns.  We just made that equal to 0.5 ms.

Here's the charge transfer for the next portion of the waveform


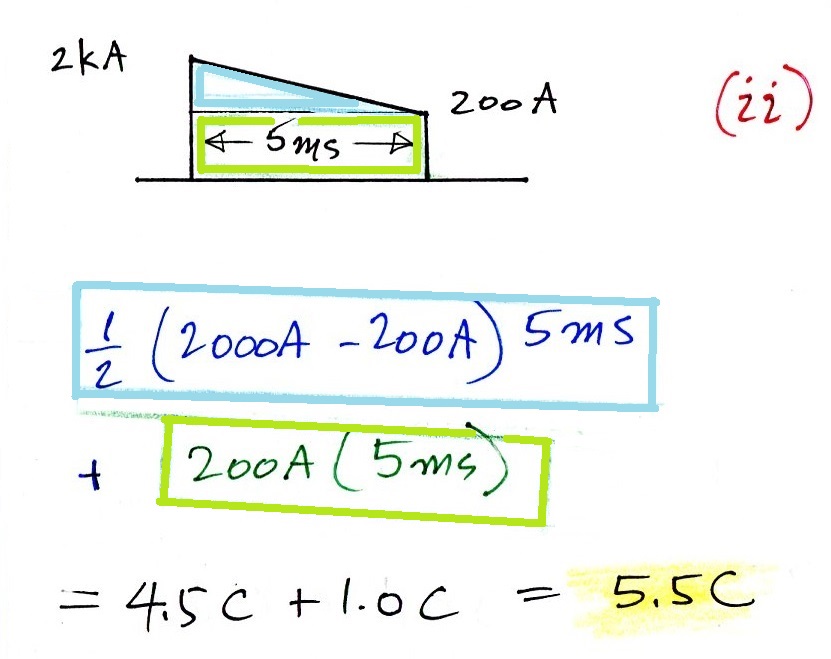
And the final portion of the waveform.  The low amplitude current last long enough that this segment transports the most charge.


#1c
This was the most time consuming part of the assignment.


Because the current is square you need to write a straight line equation for the current in each section of the waveform.  The equation for I then is squared and integrated over time.  The short 200 ns rise to peak current section is shown above. 



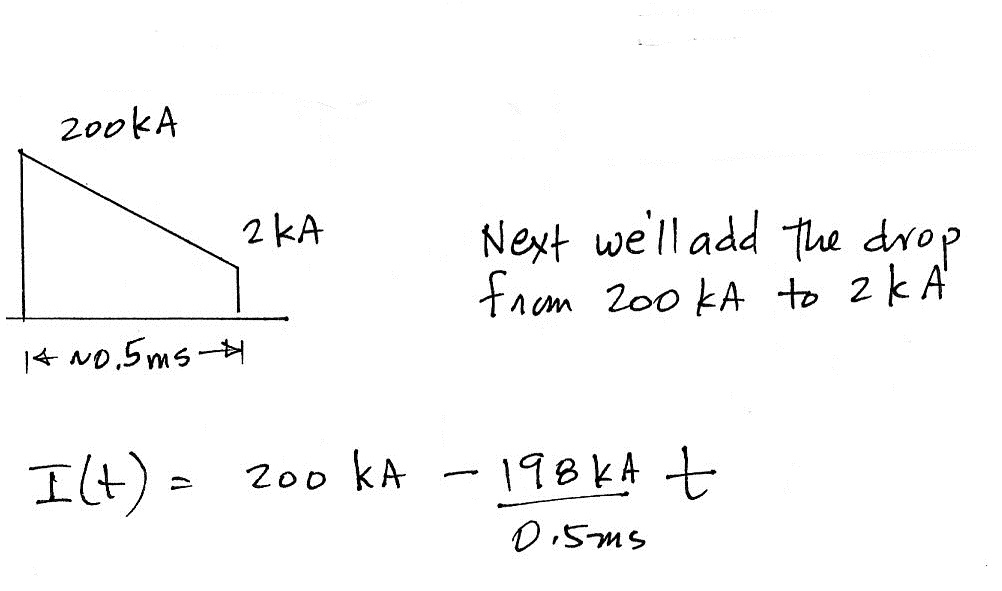
Here's the equation for the current as it decreases from 200 kA to 2 kA.  This equation then is squared and integrated.  The details are shown below.



Next we evaluate the two remaining portions of the waveform


We now only need to some the contributions from each of the three sections.



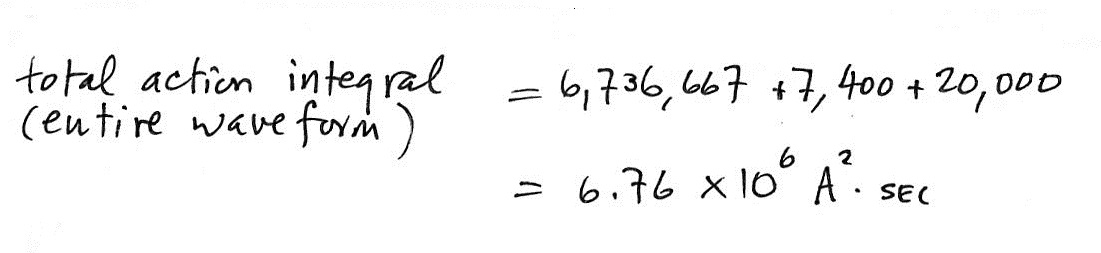
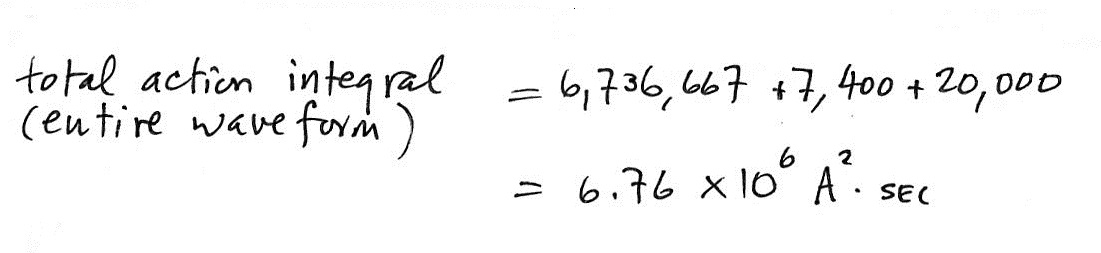
Finally in Part (d) we multiply the action integral value 10 Ω