Tue., Jan. 29, 2013
click here to download today's notes in a more printer friendly format

The first homework assignment was collected today.  I'll try to get them graded and back to you by Thursday.

A second homework assignment was distributed in class.  It will be due Thu., Feb. 7. 

Instead of meeting on Thursday at our usual time I thought we should take advantage of the seminar below.  I'm sure it will be more interesting and educational than our normal lecture and Dr. Cummins is after all the co instructor for this course.  The seminar will start at 3:30 in PAS 220 though you're welcome to come a little early for the refreshments served in PAS 546.



Here's an example of a very cleverly designed instrument that has been used to measure electric fields above the ground and inside thunderstorms (you can download the complete Winn et al. 1978 publication here). 



Two metal spheres are attached to and spin vertically around a horizontal shaft (the shaft also spins azimuthally).  The instrument is launched under a thunderstorm and is carried upward by balloon. 

As the spheres spin, a current will move back and forth between them.  The amplitude of the current will depend on the charge induced on the spheres by the electric field.  The induced charge will, in turn, depend on the intensity of the E field.
Determining how the two conducting spheres will enhance the electric field is a more complex problem than we considered in the last lecture but it has been worked out analytically (don't worry we won't be looking at the details).  You could also work it out numerically or determine the enhancement experimentally.  Note that the two spheres also act an antenna for transmitting data back to the ground.

The next figure shows an example of data obtained with an instrument like this (it is from a different publication which you can download here, but a similar instrument was used).


We're going to take a more careful look at 2 or 3 parts of the E field plot.  First the small highlighted portion at the bottom of the plot.  Here the sensor was below the lowest charge layer in the cloud (perhaps even below the base of the cloud) and the E field seems to be fairly constant varying between about -2 and -4 kV/m.  Can we use the charge density information at right in the figure to explain this field?

There are 4 layers of charge.  The field at Pt. X below the lowest layer will be a superposition of the fields from each of the layers above.   We'll assume each of the layers is of infinite horizontal extent.  We can use the integral form of Gauss' Law to determine the field above and below a layer of charge.

I think you can argue "by inspection" that the field above and below the infinite layer of charge will have just a z-component.  Also because the layer is of infinite extent the field strength will be the same at any distance above or below the layer.

So we compute ρ Δz for each of the layers, add the results together and use that to compute the field using the equation above.

Below the cloud we find that the field is negative (points downward) and has an amplitude of 3.4 kV/m.  This agrees very well with what is shown in the E field sounding.

Next we'll examine that E field change as the sensor passes through the lowest layer of charge.


We can measure the slope of the field change and the differential form of Gauss' Law to determine the volume space charge density.


Note that dE/dz is positive on the E field sounding between about 2.7 km and 4.5 km or so.  This coincides with a 1.8 km thick layer of positive space charge.  The slope turns negative between about 4.7 km and 5.1 km where there is a layer of negative charge.  The E field reaches a peak positive value at about 4.6 km, a point that is in between the layers of positive and negative charge.

We can determine the slope of the line highlighted in yellow and use that to determine the average volume space charge density in the layer of positive charge.


The value we obtain (0.27 nC/m3) is in good agreement with the 0.3 nC/m3 value given in the paper.

OK we'll leave the electrostatic stuff behind for a little while and look (again) at currents in the atmosphere.

Currents in the atmosphere and in a wire are compared at the top of the figure above.  A battery voltage drives a current through a wire and resistor in the picture at right.  In the atmosphere, at left, we normally speak of a current density (Amps/square meter) rather than current.  Positive and negatively charged "small ions" move in response to an electric field and transport charge in air (only the free electrons carry charge in a wire).  We'll refer to this as a conduction current. 

The small ions are charged nitrogen and oxygen molecules that are surrounded by water vapor molecules.  We'll look at the creation of small ions in more detail in a later lecture.

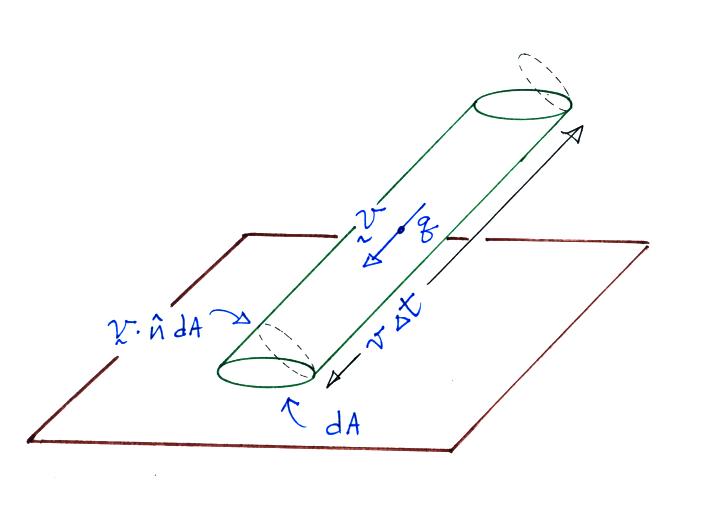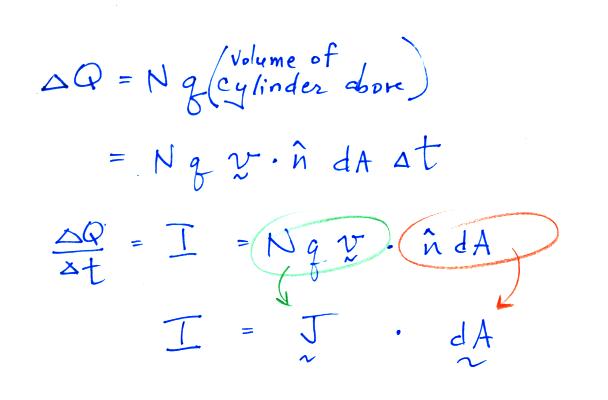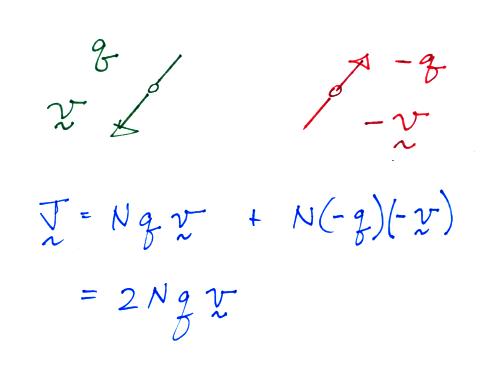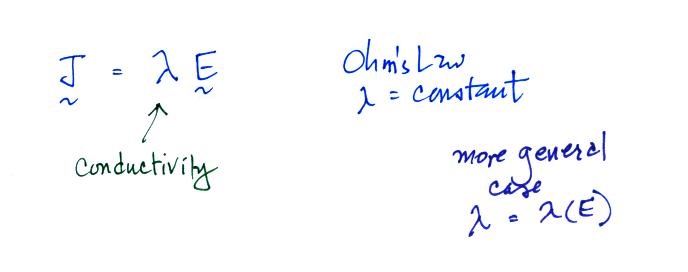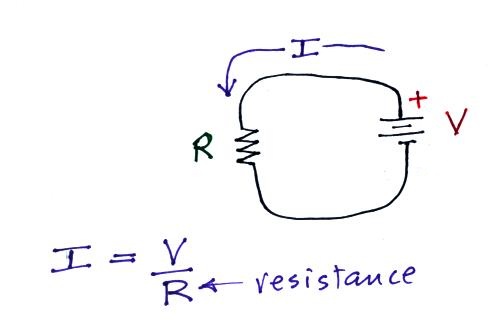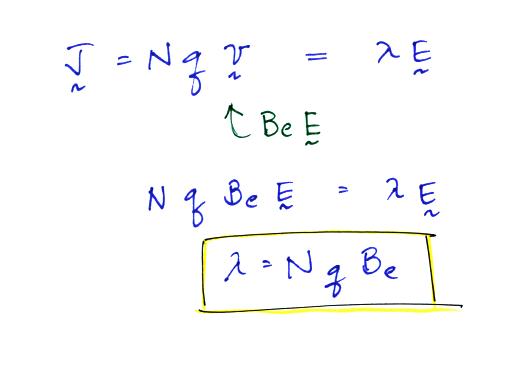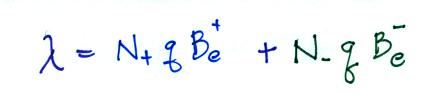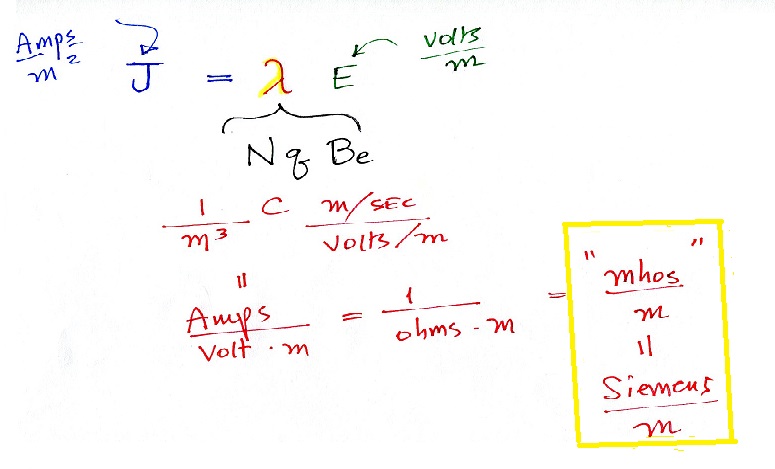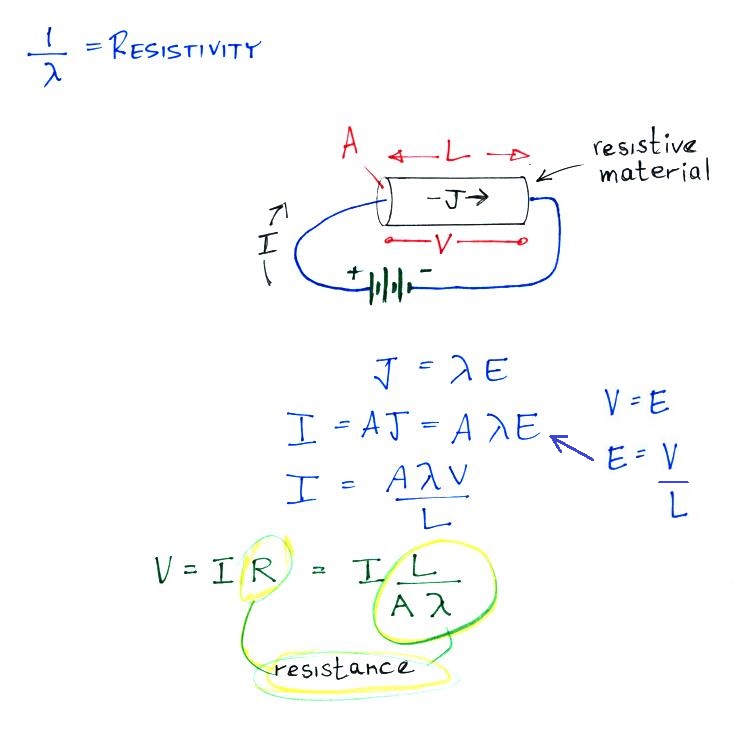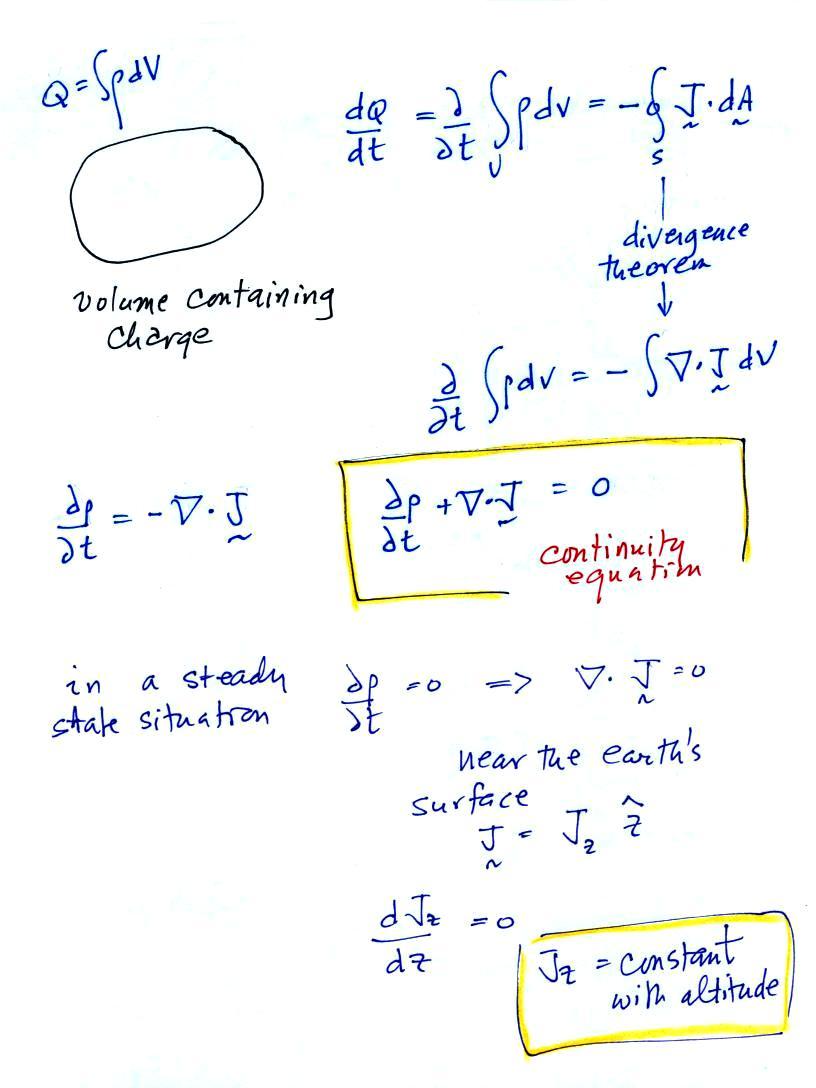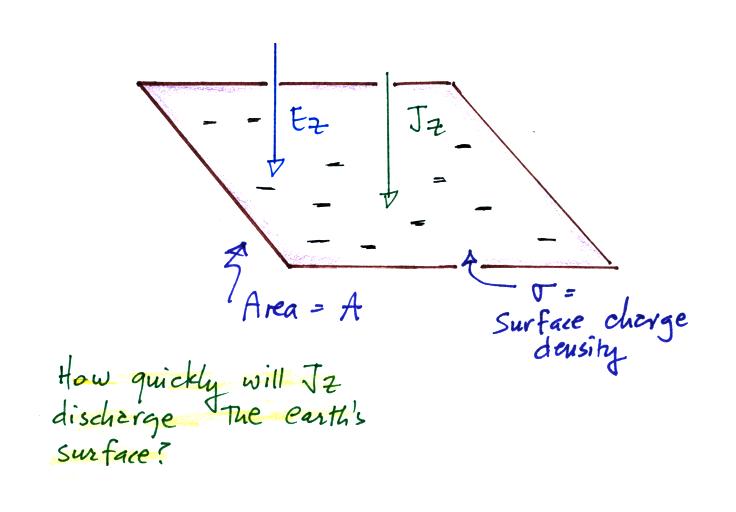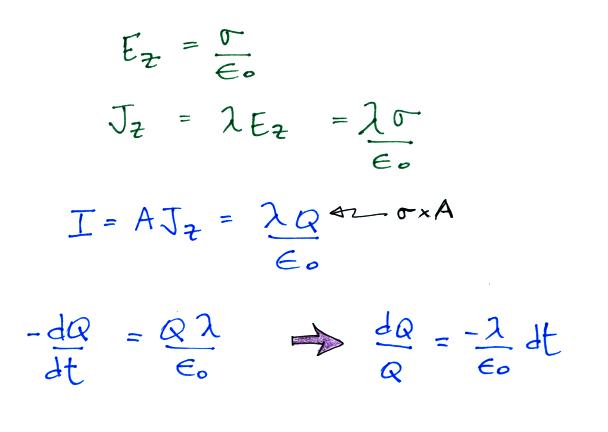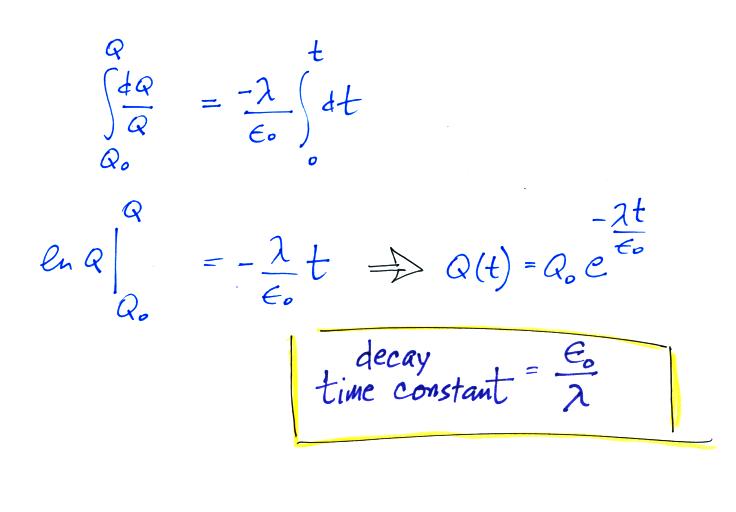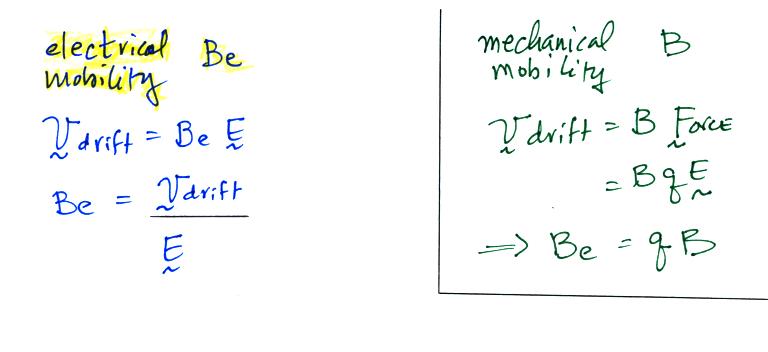
The electrical mobility is a measure of how readily charge carriers will move in an electric field.  The electrical mobility is simply the drift velocity divided by the strength of the electric field.  The relationship between electrical mobility and the mechanical mobility, which is a little more general term, is shown above.  Mechanical mobility wasn't mentioned in class.



Typical values of Be and drift velocity are shown above.  These drift velocities are much smaller than the random thermal motions of atoms and molecules in air (typically 100s of meters per second). 

Wind motions (typically a few or a few 10s of meters per second) can also potentially transport charge, but for this to occur there must be a gradient is space charge density.  These would be referred to as convection currents.


Here we consider N charge carriers (each with charge q) moving in the same direction and derive an expression for J the current density. 


In general you would need to sum contributions from different charge carriers such as carriers with +q moving in one direction and oppositely charged carriers (-q) moving in the opposite direction.



We've assumed that the number density of positive and negative charge carriers is the same and that the charge carriers carry the same charge and move at the same speed.

We will only concern ourselves with conduction currents that are linearly proportional to the electric field. 

This is known as Ohm's law and the constant of proportionality is the conductivity.  Note the similarity to Ohm's law that would apply in the earlier circuit containing a battery and a resistor.


We can use our newly derived expression for current density together with the definition of electrical mobility to obtain an expression for conductivity. 


Here we've only considered one polarity of charge carriers.  In general there will be both positive and negative charge carriers and the expression for conductivity would have two terms:

We will find that negatively charged small ions generally have slightly higher electrical mobility than positively charged small ions.  Often we will assume that the mobilities and concentrations of positive and negative charge carriers are equal in which case the conductivity would just be 2 N q Be.

A note about conductivity units.


Conductivity has units of 1/(ohms m).  In some older literature you may find this written as mhos/m (mhos is ohms spelled backwards) though Siemens/m are now the officially adopted units.

Resistivity is the reciprocal of conductivity.  Resistivity is not the same as resitance, but it is relatively easy to relate the two.


Resistivities of some common materials are listed below. 

Note how the conductivity of air is a function of air temperature.  A lightning return stroke will heat air to a peak temperature of about 30,000 K for a short time.

Later in the semester we will look at some fast time resolved measurements of lightning electric fields that were being used to try to determine characteristics of the fast time varying currents in lightning strokes.  The measurements were made in a location where propagation between the lightning source and E field antenna was over salt water to preserve as much of the high frequency content of the signals as possible.

The last thing we did in class today was to derive a continuity equation that relates changes in the space charge density in a volume to net flow of charge into or out of the volume.

Starting at upper left, the charge, Q, contained in the volume is just the volume integral of the volume space charge density.  A positive value for the surface integral of J at upper right would mean net transport of charge out of the volume.  This would reduce the total charge in the volume and dQ/dt would be negative.

We use the divergence theorem to write the surface integral of J as a volume integral of the divergence of J.  Then the two volume integrals are set equal to each other.  The only way the two integrals can be equal for an arbitrary volume is if the integrands themselves are equal.  We end up with the continuity equation highlighted in yellow.  It is then easy to show that under steady state conditions and when J has just a z component, the current density Jz is constant with altitude.

This is a constraint that you can use in the first problem on the homework assignment.


The following material was on a class handout and it was discussed only briefly at the end of class.


Now we go back to something we considered on the first day of the course.  A small portion of the earth's negatively charged surface is shown above.  Negative charge on the ground and positive charge in the atmosphere above creates a downward pointing E field.  We're now in a better position to estimate of how quickly the fair weather current would neutralize the charge on the earth's surface.

We consider the earth's surface to be a perfect conductor.  The vertical E field will depend on the surface charge density, σ.  The current density is just the product of conductivity and electric field.  We end up with a differential equation which we can easily solve for Q, the charge on an area A of the earth's surface.

If we insert reasonable values for εo and λ we obtain

This is the time for the charge on the surface to decrease to 1/e of its original value, not the time needed to neutralize it completely.