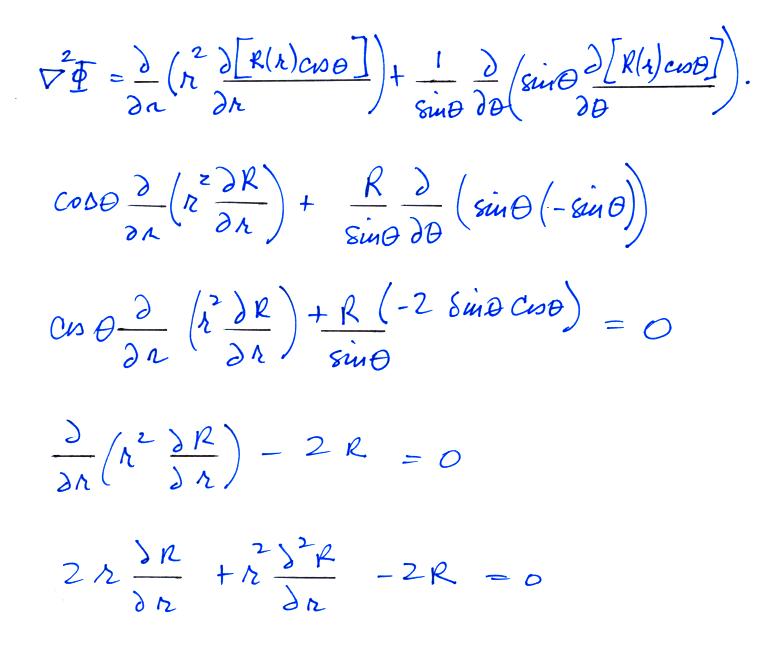
First here are a couple of sketches of
the kinds of E fields you might see from a lightning strike
to the ground (a return stroke) at relatively far range (10s
of kilometers) at left and closer range (a few kilometers
away) at right.
The close field at right is made up of several components (and we'll look at all of this in more detail later in the class)
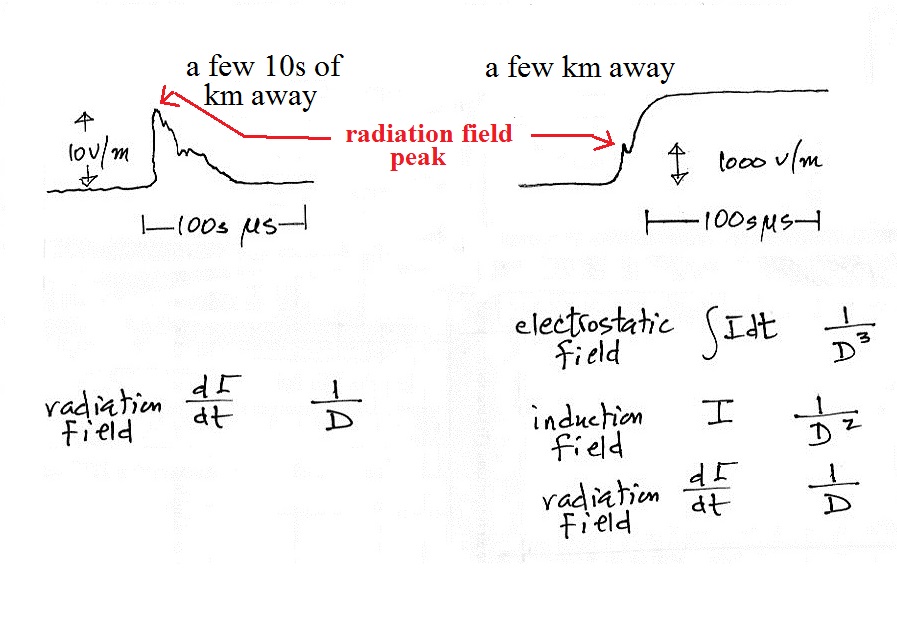
(i) an electrostatic field that is proportional to the integral of the return stroke current. This field component is slow to develop because of the integral over time. Also the 1/(distance)3 dependence means it weakens very quickly with distance. The integral of current over time is just charge. This is the field change that you see on a field mill record (the overall change from all the strokes in a flash).
(ii) a field that depends on current and decreases with a 1/(D)2dependence
(iii) the radiation field depends on dI/dt. It peaks early in the discharge as the current rises to peak value and falls off slowly with distance.
You could use a fast antenna if you were just interested in recording the very beginning of the field change. You would need a slow antenna with its longer decay time constant to faithfully record the entire field change.
The more distant field consists of just the radiation field term. A fast E field antenna alone is all you would need to measure and record a distant field like this.
The close field at right is made up of several components (and we'll look at all of this in more detail later in the class)
(i) an electrostatic field that is proportional to the integral of the return stroke current. This field component is slow to develop because of the integral over time. Also the 1/(distance)3 dependence means it weakens very quickly with distance. The integral of current over time is just charge. This is the field change that you see on a field mill record (the overall change from all the strokes in a flash).
(ii) a field that depends on current and decreases with a 1/(D)2dependence
(iii) the radiation field depends on dI/dt. It peaks early in the discharge as the current rises to peak value and falls off slowly with distance.
You could use a fast antenna if you were just interested in recording the very beginning of the field change. You would need a slow antenna with its longer decay time constant to faithfully record the entire field change.
The more distant field consists of just the radiation field term. A fast E field antenna alone is all you would need to measure and record a distant field like this.
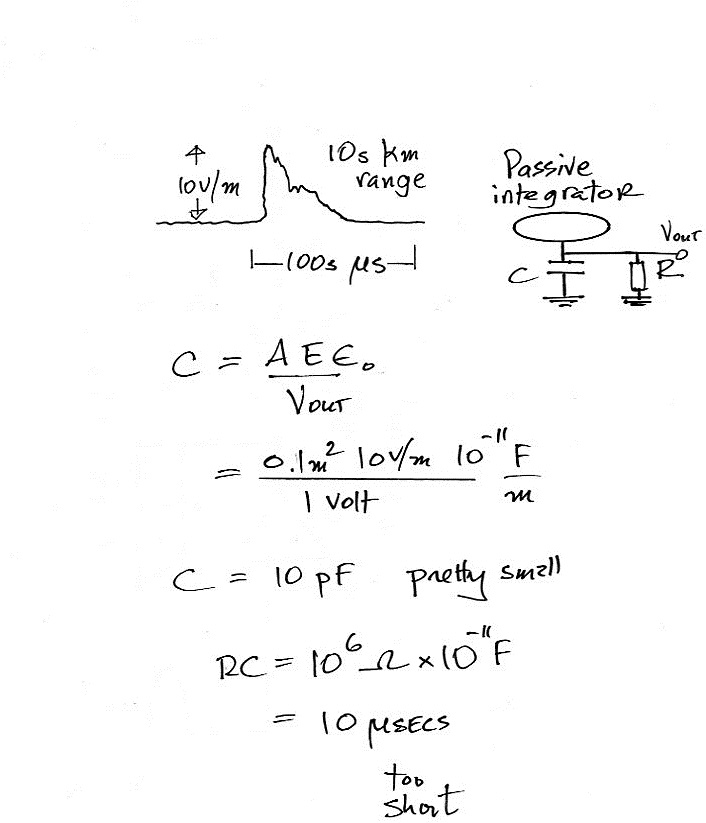
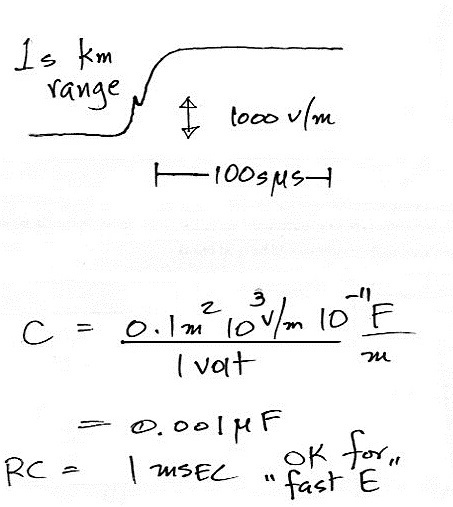
Here we're assuming a 10 V/m field change
and are estimating the value of the capacitance needed in a
passive integrator to produce an output voltage of 1 volt
(we assume the antenna area is 0.1 m2). C
would need to be 10 pF. That's pretty small, stray
capacitance in the antenna itself could be more than
that. Then when we need to connect to some kind of
measuring or recording device like an oscilloscope.
We'll assume that has an input impedance of 1 M Ω.
The resulting decay time constant, 10 μs, is too short if we
want to record a signal that lasts for 100 μs or
more.
In a case like this the antenna needs to be connected to an active integrator as shown below.
Here's another problem you probably worked out in an
electricity and magnetism class. We're going to
determine how an initially
uniform electric field, Eo, is distorted by the
presence of an uncharged conducting sphere. Charge is
induced on the surface of the sphere and it moves around
until the field inside the sphere becomes zero.
The sphere distorts the field in such a way that the field
lines are everywhere normal to the surface of the
conductor.
In an E & M class this problem is included as an example of solving Laplace's equation. Here our main interest is in the final result rather than all the details of the calculation.
We'll use spherical polar coordinates and place the origin of our coordinate system at the center of the sphere,
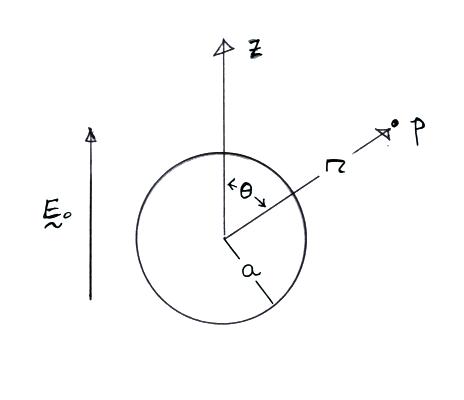
There is azimuthal symmetry, so the potential and the electric field depend on r and θ only. We can proceed to solve Laplace's equation for the potential, Φ, subject to the following boundary conditions
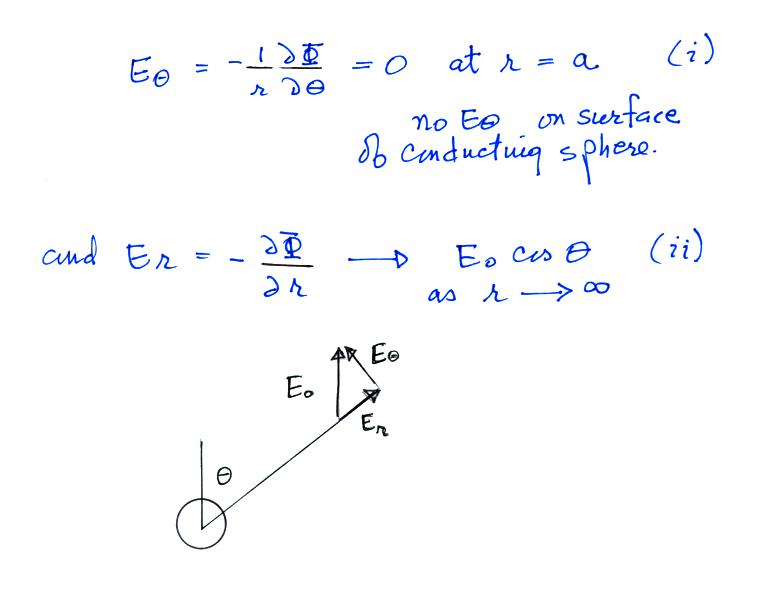
(i) There is no tangential, θ, component of the
E field at the surface of the sphere, just an r
component that is perpendicular to the surface.
(ii) The second condition is just that as you move well away from the sphere the r and θ components of the field add up to produce Eo pointing in the z direction
In the spherical coordinate system
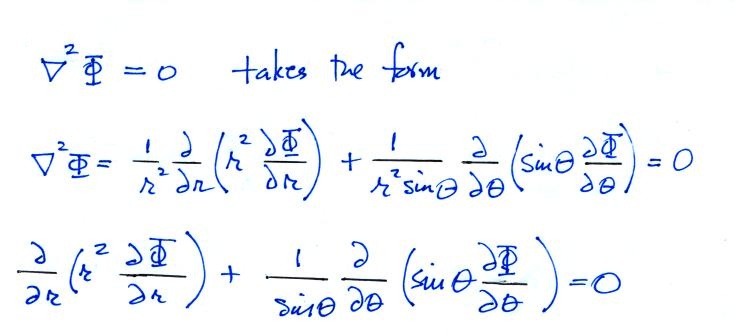
Assuming the variables are separable, we try a general solution of the form:
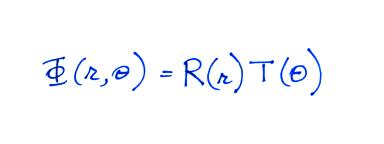
Just looking at the boundary condition (Eqn. (ii)), we
simply try a T(θ)
function of the form
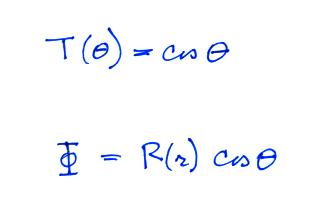
Now, inserting this into our original differential equation, we find
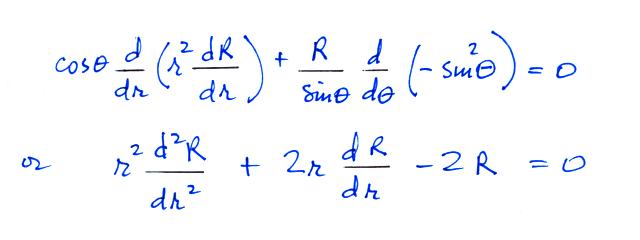
and
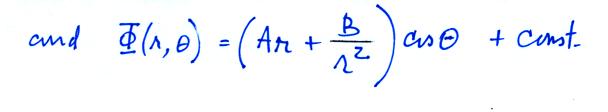
Now,
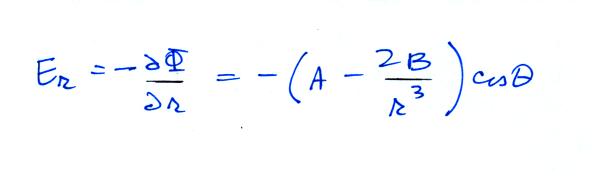
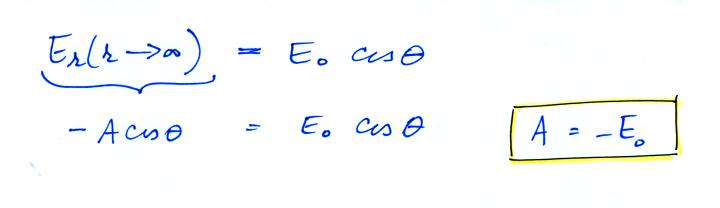
next we make use of the other boundary condition. We need to find the θ component of the field and then set r = a

and our potential function is now
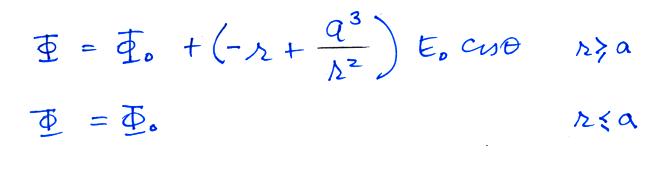
with this Φ our electric field components are:
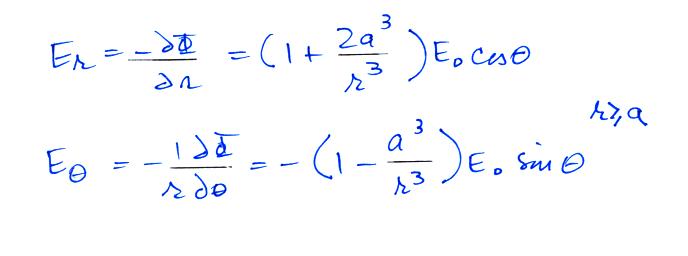
and the surface charge density is
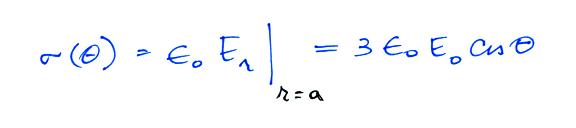
Our main interest in this result is that the sphere has enhanced the value of the ambient field at the top and bottom surface of the sphere by a factor of 3.
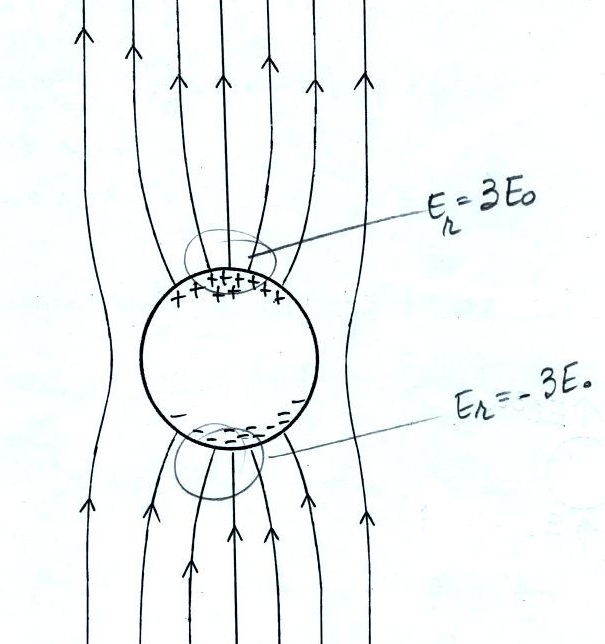
This figure gives you a rough idea of how the field is changed in the vicinity of the sphere. E field lines must intersect the sphere perpendicularly. The field is amplified by a factor of three at the top and bottom of the sphere.
This factor of 3 enhancement does not depend on the diameter of the sphere.
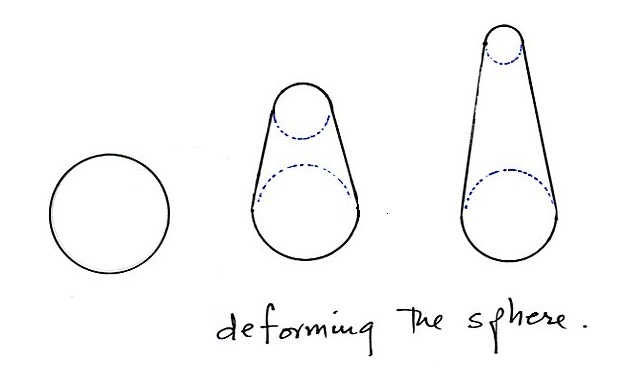
What if we were to stretch the sphere vertically in such
a way that one part ends up with more of a point than the
other. It would be very hard to determine the field
enhancement of an object like this analytically, it would
probably be much easier to do it numerically.
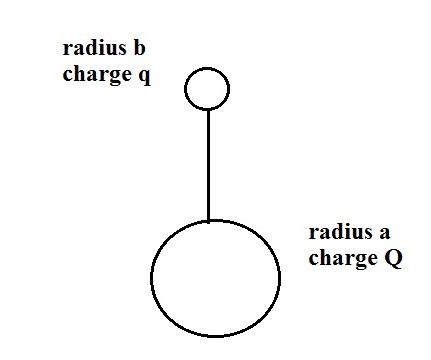
To get some feeling for how the field enhancement at the
top and bottom of an object like this would differ, Noble
prize winner Richard Feynman considers two separate
spheres with different radii and then connects them with a
wire so they are at the same potential.
You'll find Feynman's discussion here (Sect. 6-11, the "method of images" is also discussed in Chapter 6).


Lightning also strikes aircraft. Here's an example. Often, probably usually, the discharge is initiated by the airplane.
We'll talk about rocket triggered lightning later in the course. I'm referring to lightning that is purposely triggered so that it can strike instrumentation on the ground and studied at close range.
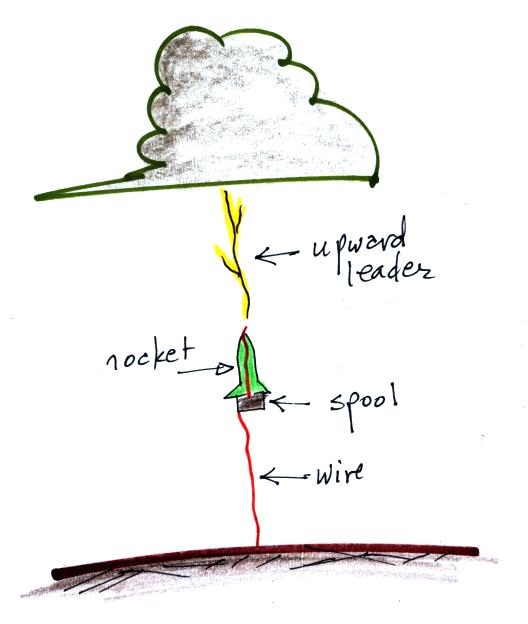
The basic idea is to launch a small rocket (about 3
feet tall) in a high electric field under a
thunderstorm. A spool of wire is mounted on the tail
fins of the rocket. One end of the wire is connected
to ground and the other end runs up to the nose of the
rocket. The wire un-spools (probably the hardest
part is to keep the wire from breaking and keeping the
wire from pulling the rocket to one side or another) once
the rocket is launched forming a narrow tall conducting
object. Field enhancement at the top of the rocket
is enough often times to initiate an upward leader
discharge that then triggers lightning.
Here's an example from the ICLRT (International Center for Lightning Research and Testing) operated by the University of Florida.
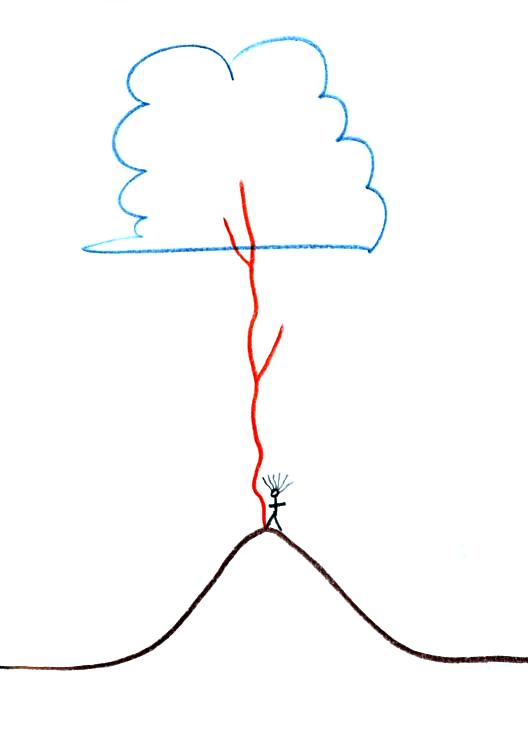
Note the direction of the branching. This indicates
that this discharge began with a leader process that
traveled upward from the mountain. Most cloud to
ground lightning discharges begin with a leader that
propagates from the cloud downward toward the ground.
We will of course look at the events that occur during
lightning discharges in a lot more detail later in the
semester. Here
are some examples filmed in Germany (probably
developing off tall towers of some kind, perhaps wind
turbines) and strikes
to the Empire State Building.
The E fields on mountain tops under a thunderstorm can be strong enough to lift a person's hair as illustrated below. This is a very dangerous situation to be in.
I've only recently found the source of these images. The two boys on the right were brothers. The younger boy was struck by lightning and suffered 3rd degree burns on his back. Another person in the area was killed by a lightning strike. The girl on the left is, I believe, a friend of the two boy's sister. You should really have a look at the article.
And finally the ability of a point to draw off or throw off electrical charged that so interested Benjamin Franklin involves enhancement of the E field.
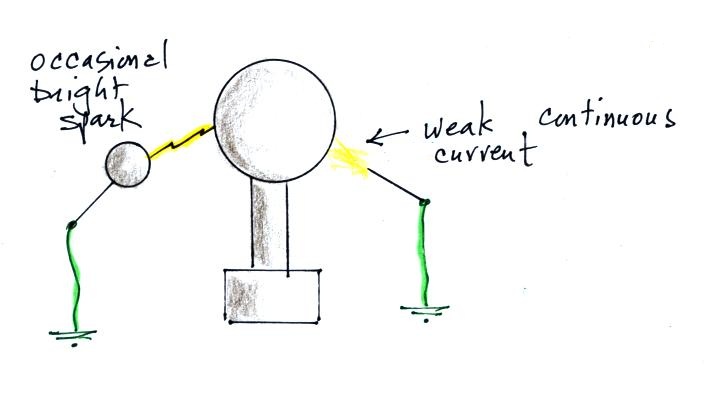
A pointed conductor brought near a Van de Graaff generator enhances the field enough to ionize air, create charge carriers, and make the air more conducting. A weak current flows between the Van de Graaff and the point. Charge on the generator is not able to build to the point where a large bright spark occurs.
Some of the details of one of the earlier calculations are shown below:
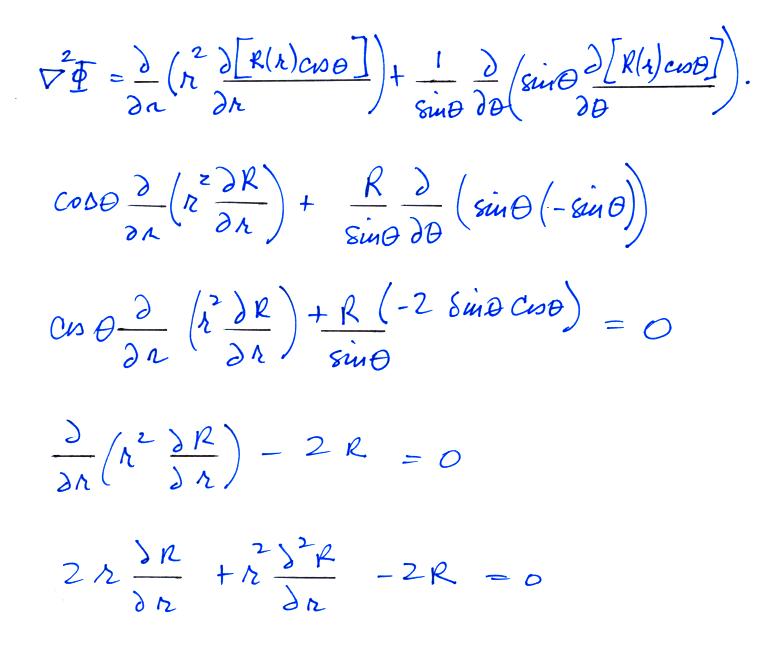
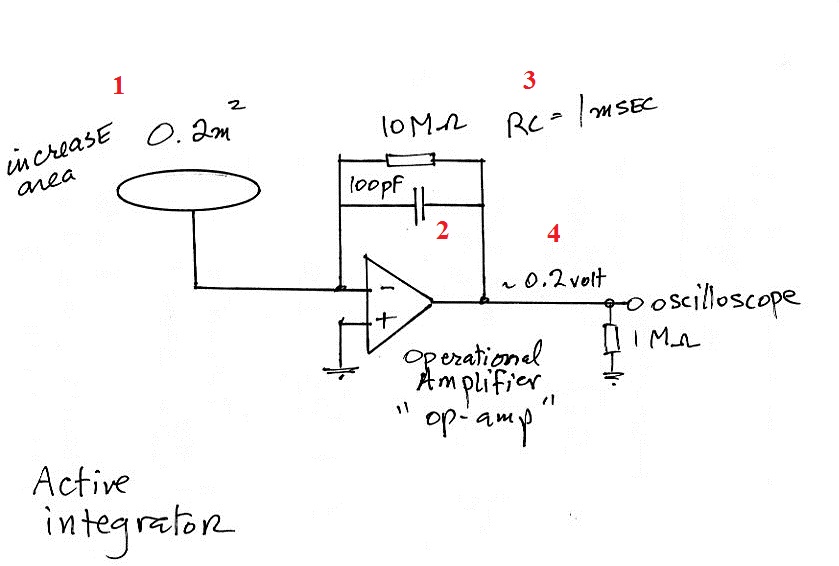
In a case like this the antenna needs to be connected to an active integrator as shown below.

We've also made the antenna area a
little larger to increase the gain of the system (Pt.
1). Instead of 10 pf, we've used a 100 pF
capacitor in the feedback look of the op-amp (Pt.
2). The decay time constant is determined by the
product of R and C in the feedback loop (Pt. 3) and
doesn't depend on the input impedance of the
oscilloscope. A 10 V/m E field signal would
produce a 0.2 volt output signal in this case.
A passive integrator circuit would work for the closer discharge.
A passive integrator circuit would work for the closer discharge.

Because of the larger E field
signal, a larger capacitor can be used. The
decay time constant in this case is 1 ms, which is
suitable for a fast E antenna system (again we've
assumed a 1 M Ω.
oscilloscope input impedance).
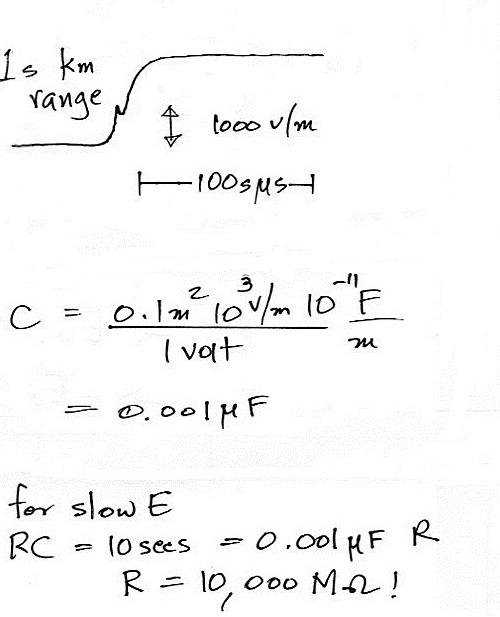
A slow E field antenna system would be needed to faithfully record the longer duration field variations in these nearby discharges. We'll assume a 1000 V/m field change and determine the value of the capacitance needed to produce a peak output of 1 volt.
A slow E field antenna system would be needed to faithfully record the longer duration field variations in these nearby discharges. We'll assume a 1000 V/m field change and determine the value of the capacitance needed to produce a peak output of 1 volt.

A much larger resistance is needed
across the integrating capacitor to increase the decay
time to 10 seconds. You can find resistances
this large. But when the passive integrator is
connected to a recorder the 1 M Ω input
impedance of the recorder in parallel with the 10,000
M Ω resistor would lower to overall resistance to
about 1 M Ω. An active integrator
circuit is needed here also.

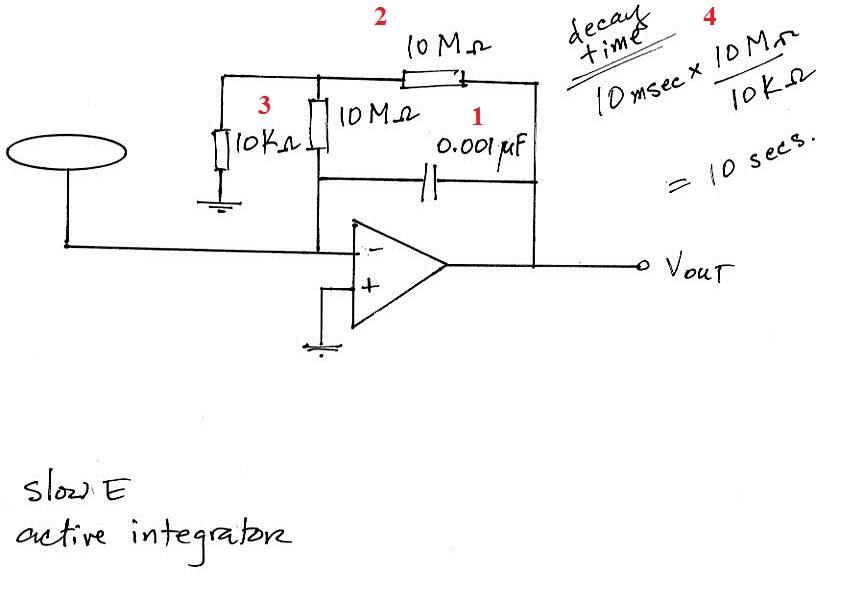
We've used the same
0.001 μF integrating capacitor (Pt. 1) with a
10 M Ω
resistor in parallel (Pt. 2). Two additional
resistors have been added to the circuit (Pt.
3). The effect they have is to multiply the
10 ms decay time by a factor of 1000 resulting in
a 10 second decay time. That's a very
reasonable value for a slow E antenna.
Don't worry about all the circuit details. I've included them just to illustrate some of what needs to be considered when designing these E field antenna systems.
Don't worry about all the circuit details. I've included them just to illustrate some of what needs to be considered when designing these E field antenna systems.
Conducting Sphere in a
Uniform Electric Field
In an E & M class this problem is included as an example of solving Laplace's equation. Here our main interest is in the final result rather than all the details of the calculation.
We'll use spherical polar coordinates and place the origin of our coordinate system at the center of the sphere,

There is azimuthal symmetry, so the potential and the electric field depend on r and θ only. We can proceed to solve Laplace's equation for the potential, Φ, subject to the following boundary conditions

(ii) The second condition is just that as you move well away from the sphere the r and θ components of the field add up to produce Eo pointing in the z direction
In the spherical coordinate system
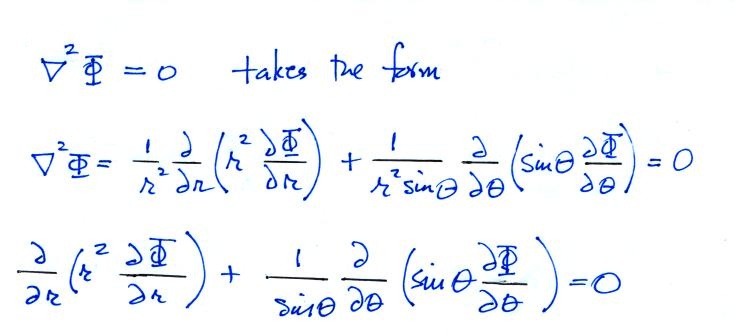
Assuming the variables are separable, we try a general solution of the form:
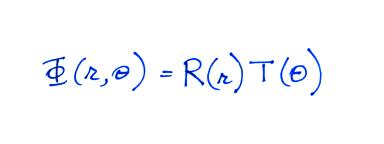
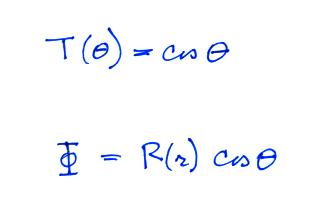
Now, inserting this into our original differential equation, we find
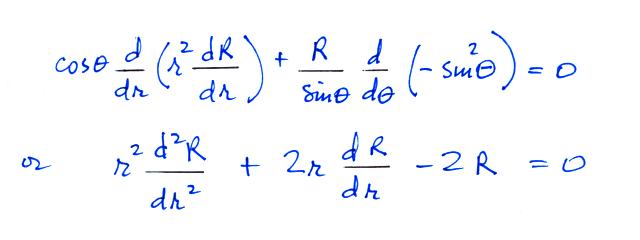
Some of the missing
intermediate details are appended at the end of this
section.
Now, let's try a solution to the R equation of the form

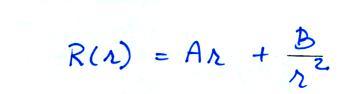
Now, let's try a solution to the R equation of the form

When we substitute
this into the differential equation above we get
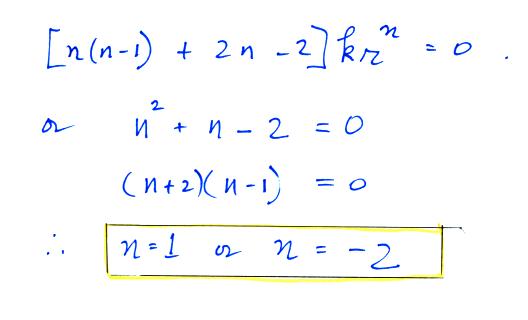
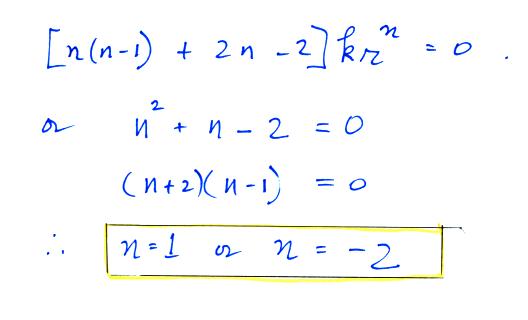
Now a general
R solution will be of the form
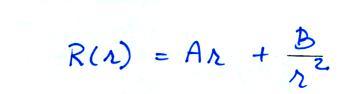
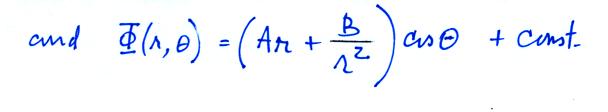
Where A and B must be
determined from the boundary conditions.
Now,
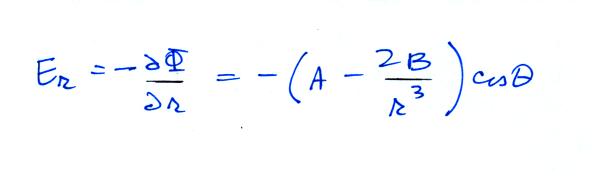
applying boundary
condition (ii) as r goes to infinity
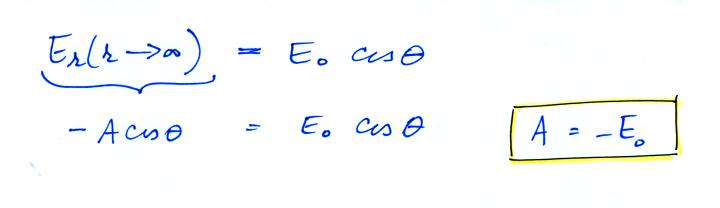
next we make use of the other boundary condition. We need to find the θ component of the field and then set r = a

and our potential function is now
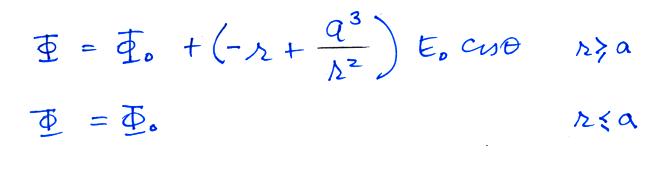
with this Φ our electric field components are:
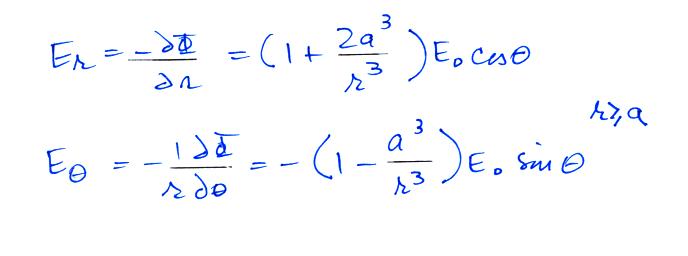
and the surface charge density is
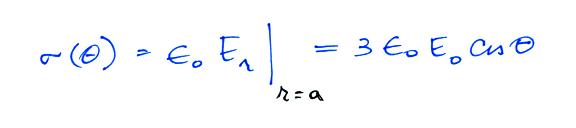
Our main interest in this result is that the sphere has enhanced the value of the ambient field at the top and bottom surface of the sphere by a factor of 3.

This figure gives you a rough idea of how the field is changed in the vicinity of the sphere. E field lines must intersect the sphere perpendicularly. The field is amplified by a factor of three at the top and bottom of the sphere.
This factor of 3 enhancement does not depend on the diameter of the sphere.


You'll find Feynman's discussion here (Sect. 6-11, the "method of images" is also discussed in Chapter 6).
I had a little trouble
understanding what he was doing the first time I read it
so here's some additional information.

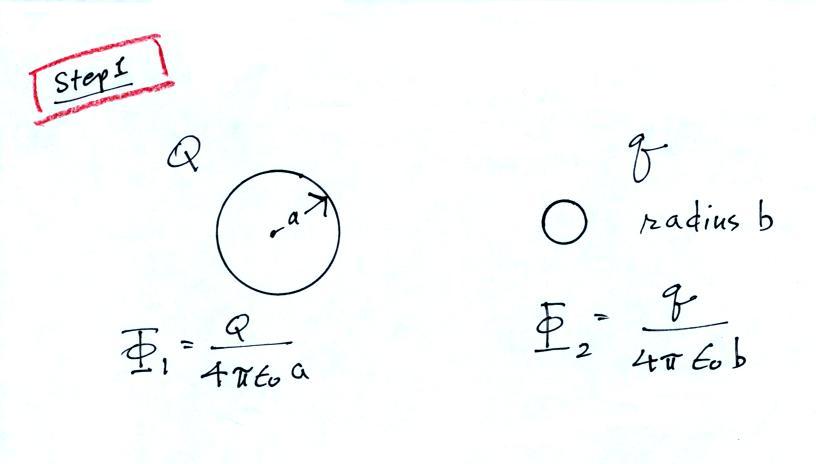
In the first step we
consider two spheres. The larger sphere carries a
charge Q, the smaller one a charge q. At this point
they are unconnected. We write down the potential at
the surface of each

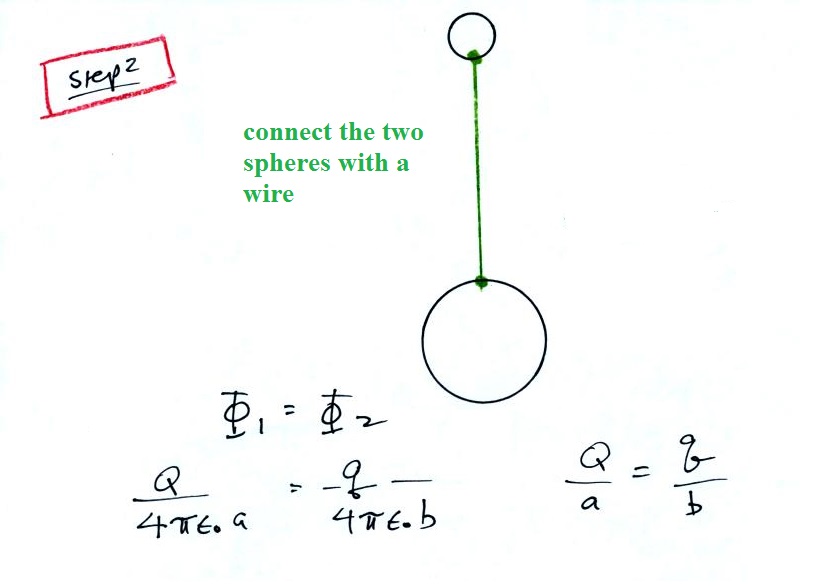
Next we connect the two
spheres with a wire which forces the two potentials to be
equal (this would of course cause the charge to rearrange
themselves and turn this into a much more complex problem,
but we will ignore that).

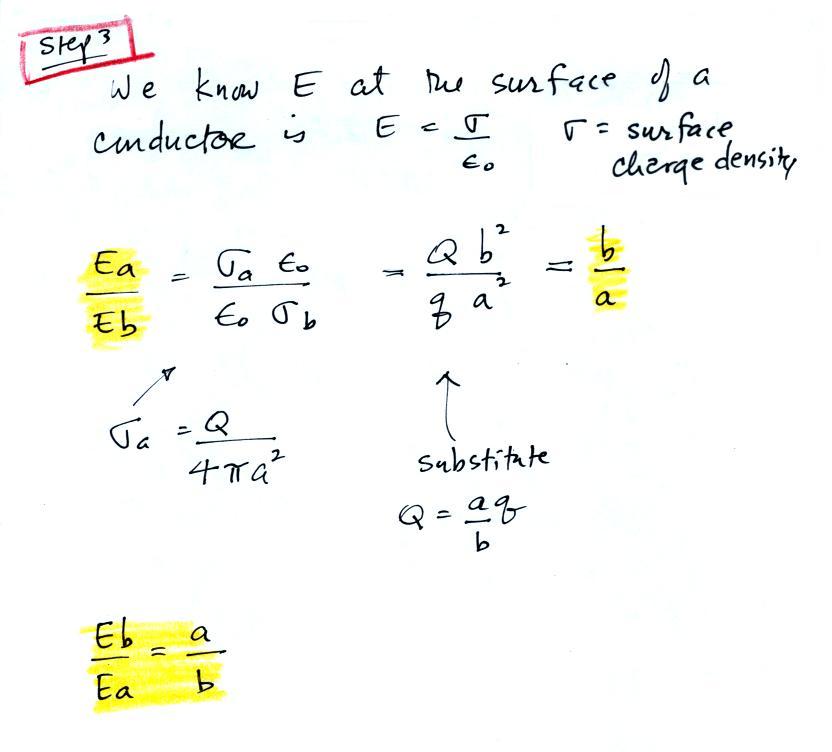
In this last step we make
use of the E = σ/εo
relation for the E field at the surface of a conductor and
write down an expression for Ea divided by Eb. We
assume Q is spread out uniformly around the larger sphere
(unrealistic but that's what we'll do). The surface
charge density σa
for the larger sphere is Q divided by the surface area of
the larger sphere (4πa2). For the smaller
sphere σb
is q divided by 4πb2. We see
that the field at the surface of the smaller sphere is a/b
times larger than the field at the surface of the bigger
sphere. Since a > b, the field above the smaller
sphere is enhanced.
Here is a real example of field
enhancement that lead to triggering of a lightning strike
and subsequent loss of a launch vehicle (you'll find the
entire article here)

In this case the rocket body together
with the exhaust plume created a long pointed conducting
object. Enhanced fields at the top and bottom
triggered the lightning discharge. Note the branches
point away from the rocket. This indicates that the
leader process at the beginning of the discharge started
at the object and moved outward.

Lightning also strikes aircraft. Here's an example. Often, probably usually, the discharge is initiated by the airplane.
We'll talk about rocket triggered lightning later in the course. I'm referring to lightning that is purposely triggered so that it can strike instrumentation on the ground and studied at close range.

Here's an example from the ICLRT (International Center for Lightning Research and Testing) operated by the University of Florida.
Enhancement of the E field at the top
of a mountain (or tall building or structure) is sometimes
high enough to trigger lightning also.

The E fields on mountain tops under a thunderstorm can be strong enough to lift a person's hair as illustrated below. This is a very dangerous situation to be in.
 |
 |
I've only recently found the source of these images. The two boys on the right were brothers. The younger boy was struck by lightning and suffered 3rd degree burns on his back. Another person in the area was killed by a lightning strike. The girl on the left is, I believe, a friend of the two boy's sister. You should really have a look at the article.
And finally the ability of a point to draw off or throw off electrical charged that so interested Benjamin Franklin involves enhancement of the E field.

A pointed conductor brought near a Van de Graaff generator enhances the field enough to ionize air, create charge carriers, and make the air more conducting. A weak current flows between the Van de Graaff and the point. Charge on the generator is not able to build to the point where a large bright spark occurs.
Some of the details of one of the earlier calculations are shown below: