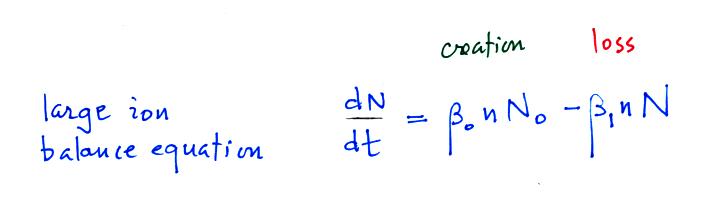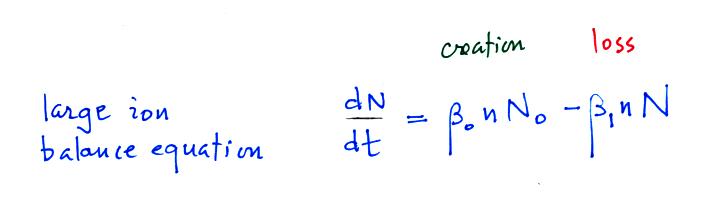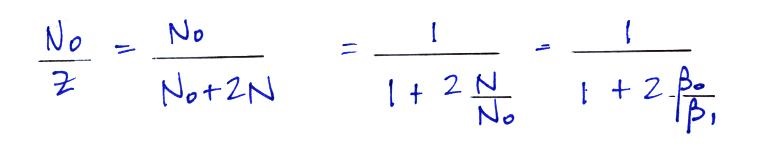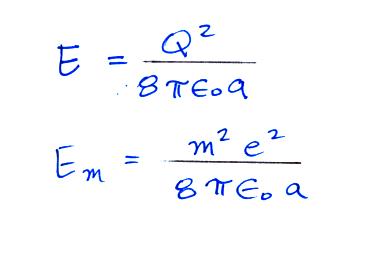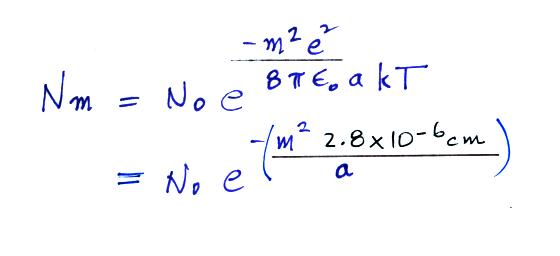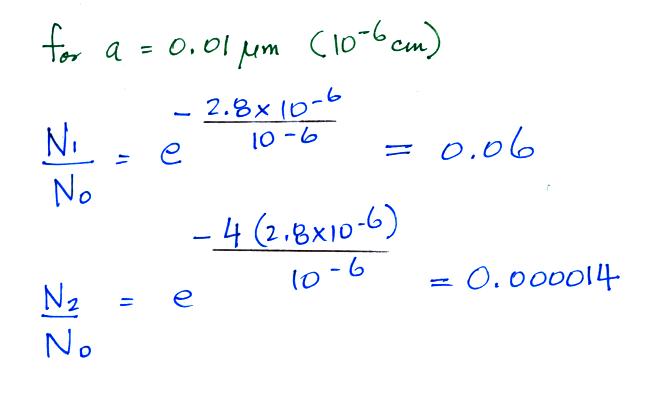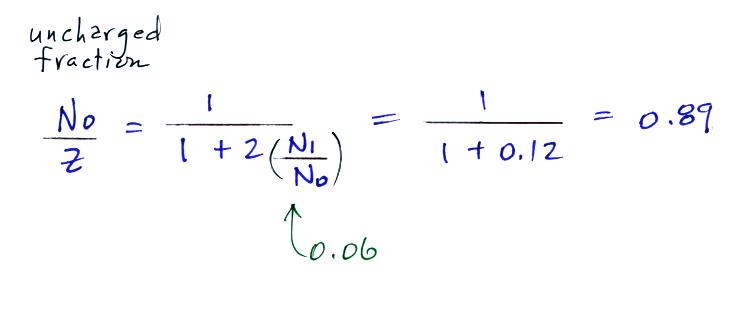Here we will spend some time considering what fraction of
particles are uncharged and charged. We'll start with a
large ion (charged particle) balance equation.
N in this equation can represent
the concentration of either positively or negatively charged
particles. Large ions are created when a small ion
attaches to an uncharged particle. They are destroyed when
a small ion attaches to a charged particle of the opposite
polarity .
Under steady state conditions
Now we'll look at the fraction of large and small particles that
are uncharged.
In some supplementary
notes we look at how a relatively straight forward solution
to the diffusion equation can be used to derive an expression
for β0.
You can then consider the additional flux of small ions to a
charged particle (diffusion plus the effect of the electric field
created by the charged particle). That gives an expression
for β1 . For
larger particles we find that β0 = β1 .
For larger particles you would expect to find equal numbers of
positively charged, negatively charged, and non-charged particles.
For smaller particles
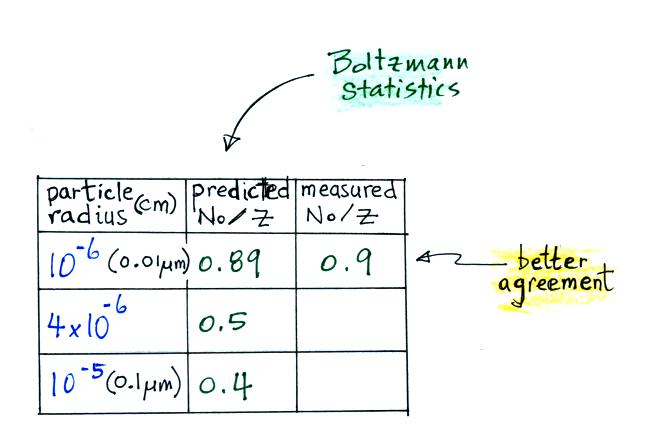
the agreement between predictions and measurements of the
uncharged fraction (No/Z) is not very good.
Because of this poor agreement we did not spend any class time
working through the details of the diffusion theory approach to
estimating particle attachment coefficients. The details are
in the supplementary
reading though if you are interested.
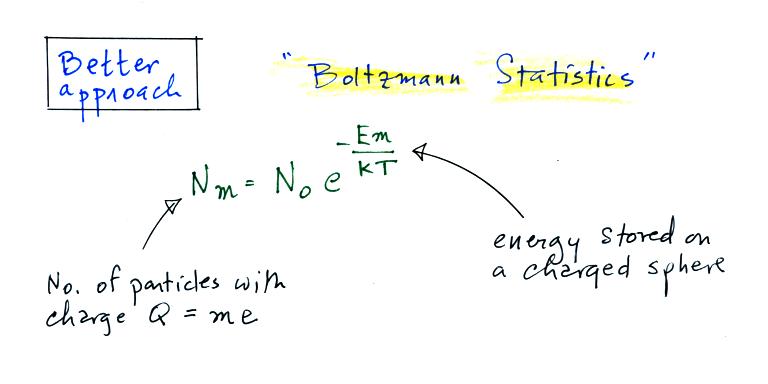
We will have a more careful look at an alternate approach that
uses Boltzmann statistics.
A charged particle has a certain amount of "stored" energy
associated with it. Thus we can use the Boltzmann
distribution above to predict the distribution of charged
particles (the particles can carry only integral multiples of an
electronic charge, i.e. Q = me, where m is an integer and e is the
charge on an electron).
The energy stored on a charged sphere is (the details of the
derivation are in a second
set of supplementary notes)
We can insert this expression into the Boltzmann distribution
equation above.
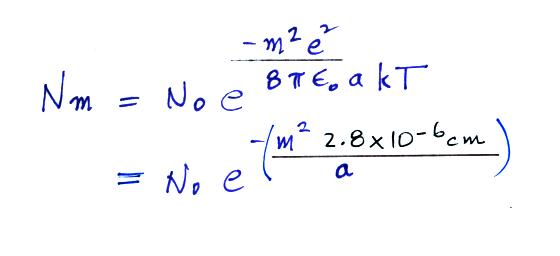
A temperature of 300 K was
assumed in the calculation above. Also in class I used
0.028 μm in the parentheses instead of 2.8 x 10 -6
cm. The exponential starts to become pretty small for
particles with radii less that 2.8 x 10-6 cm, less than 0.028
μm (especially if m > 1, that is the particle has
more than one electronic charge). So we can see that
most small particles will be uncharged. Those that are
charged will mostly just carry 1 electronic charge. For
example
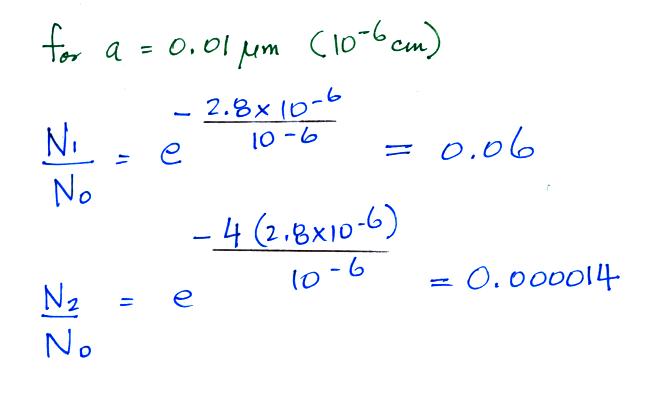
Now we can compare
predictions of the uncharged fraction of particles with
measurements. Here are the details of the predicted
value for a particle with radius = 10-6 cm.
The agreement between measured and predicted values is much
better. Again, if the table had been extended to larger
particles, we would expect the predicted No/Z to approach 0.33.