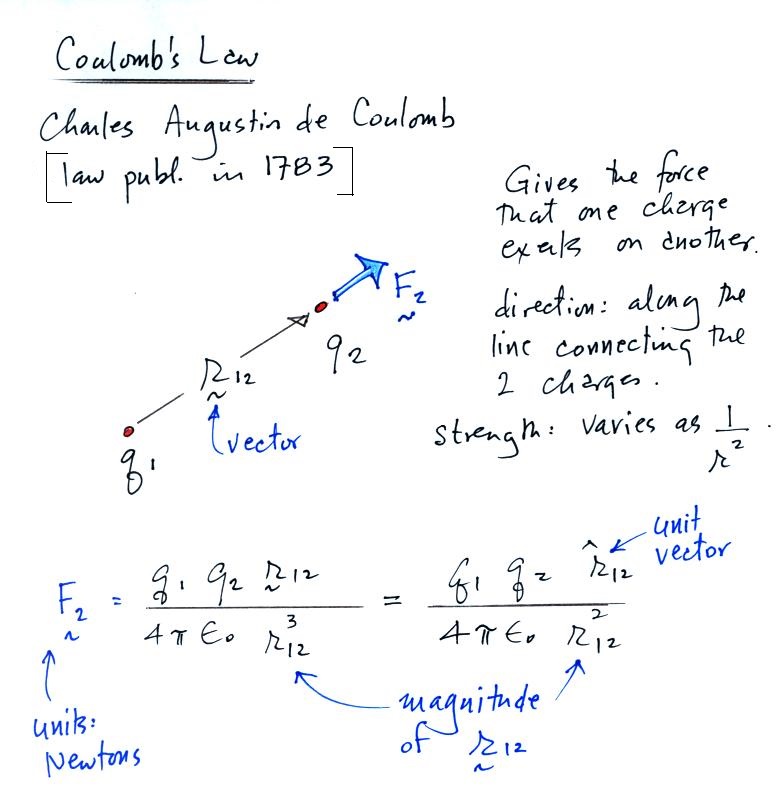
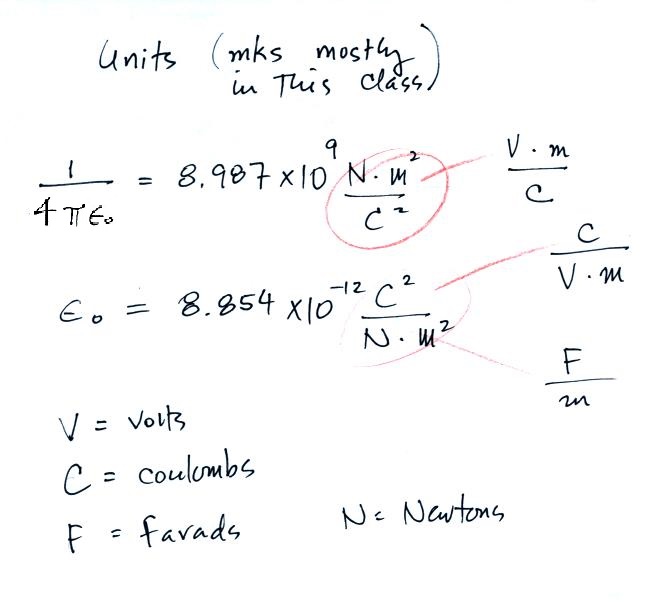
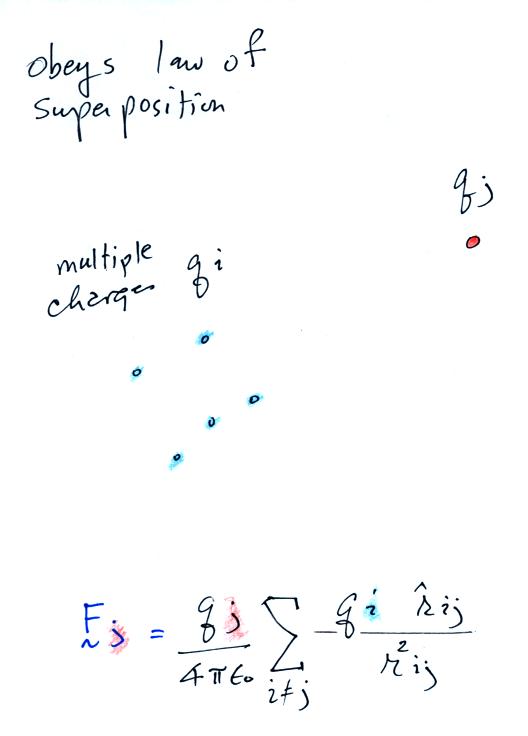
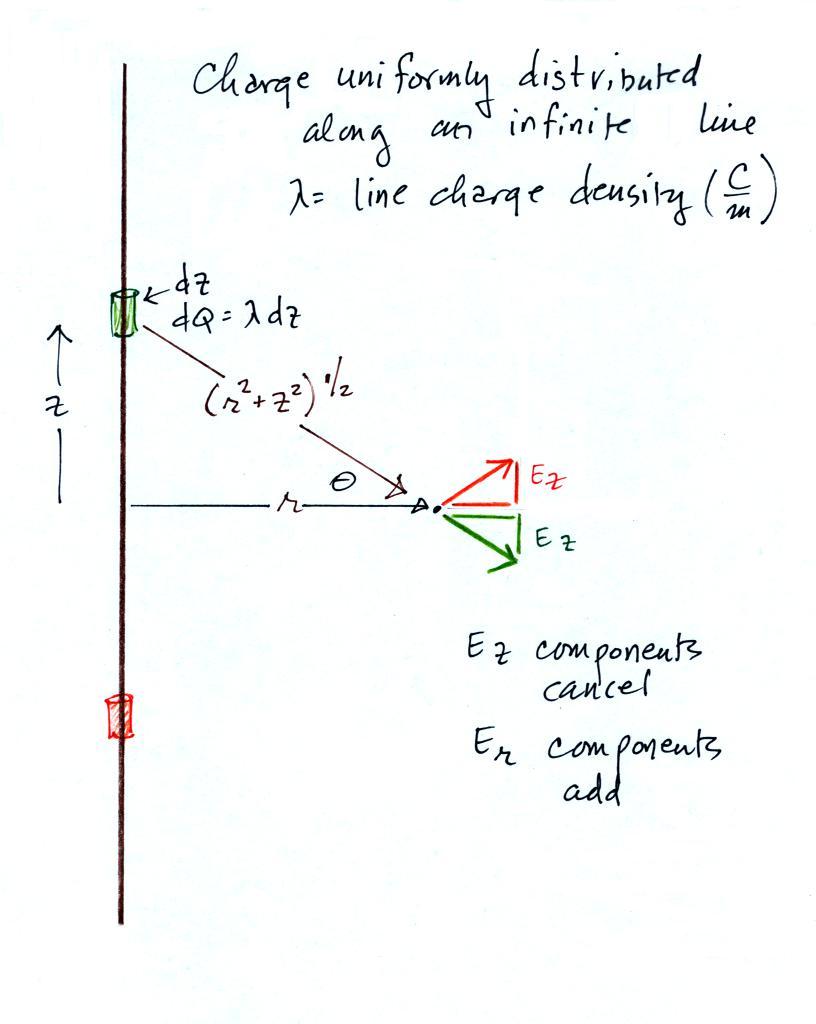
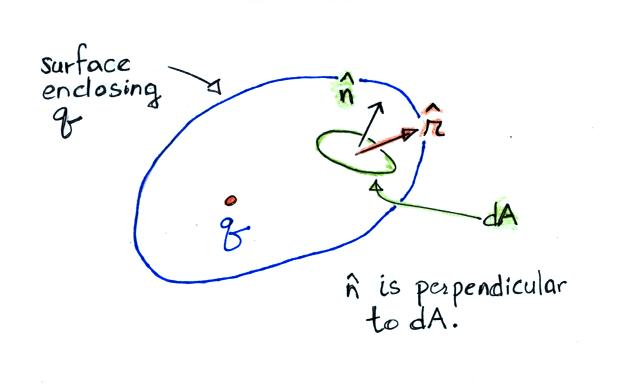
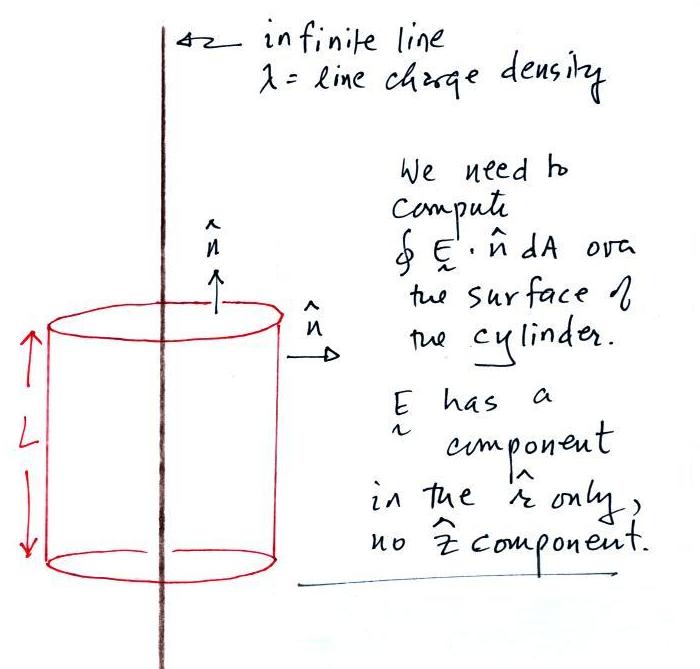
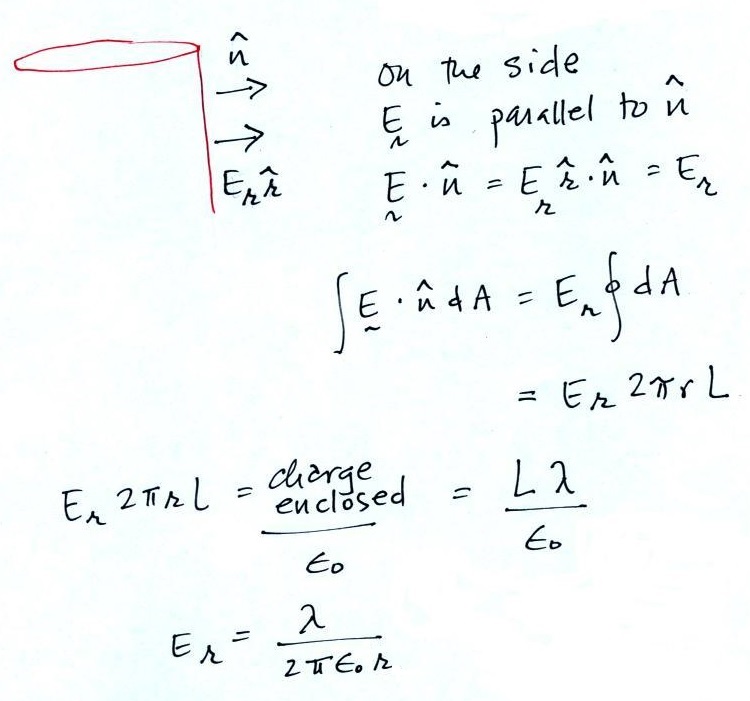
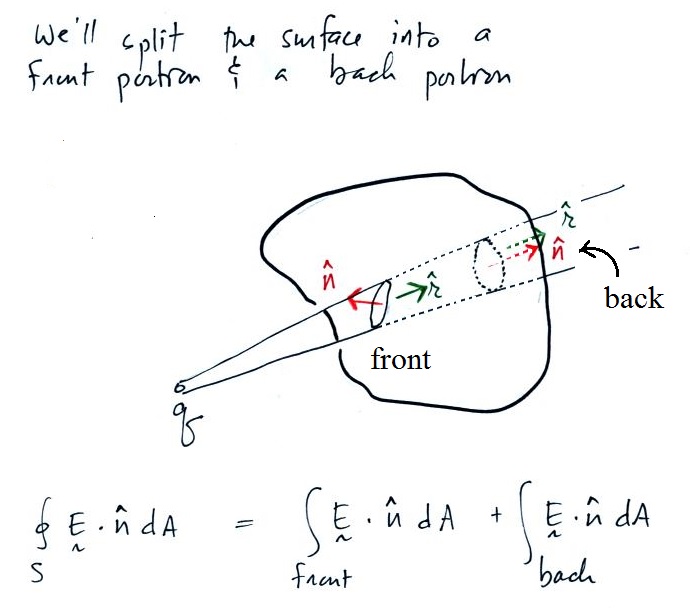
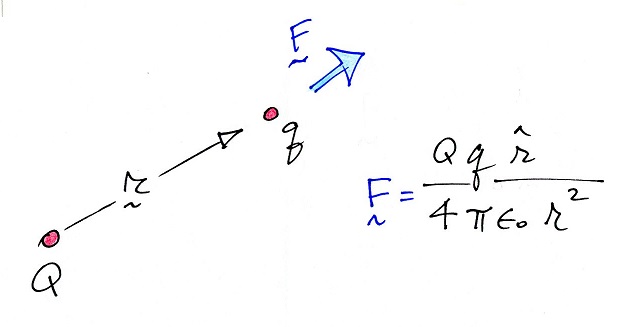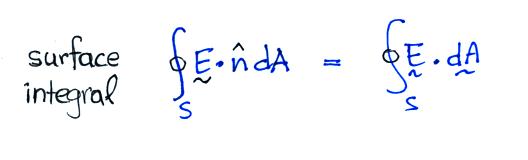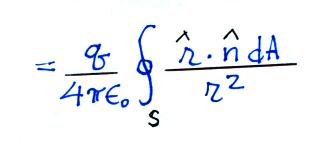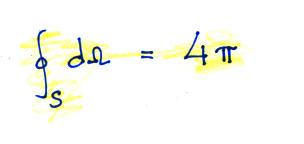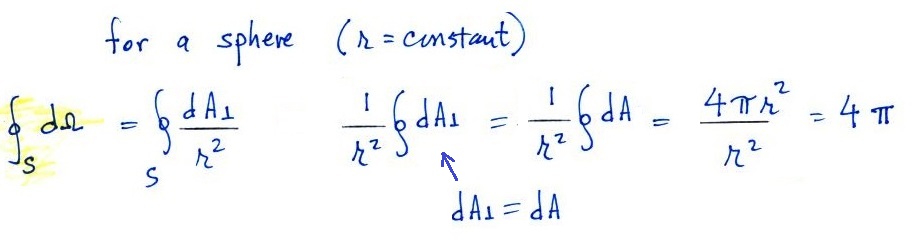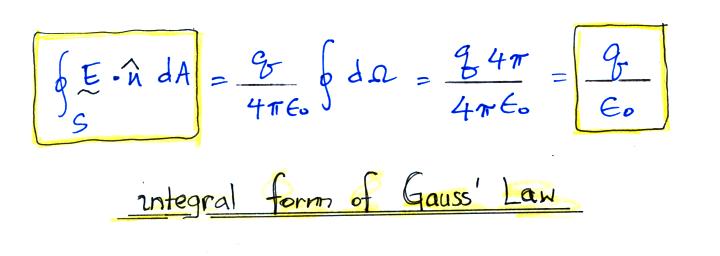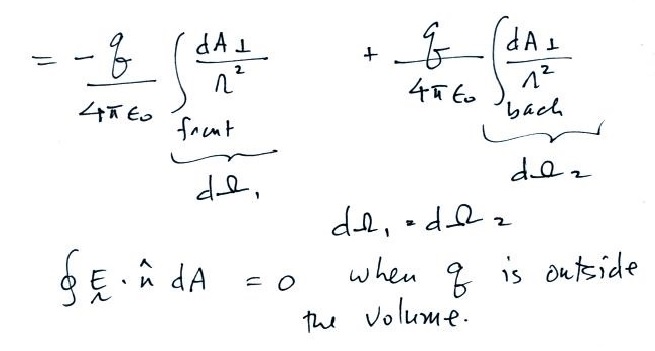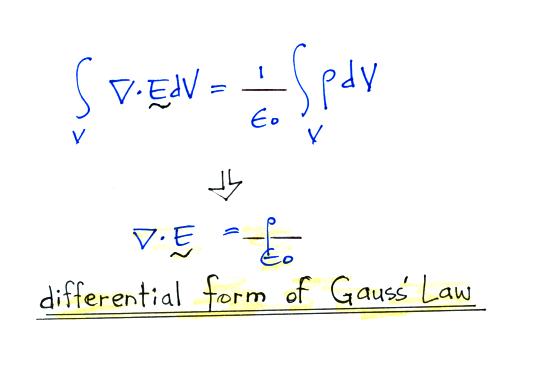Substituting in the expression
for electric field surrounding a point charge.
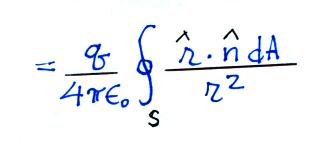
This could be a difficult
integral to evaluate for a surface of arbitrary shape.
However we can first note that the surface integral can be
rewritten as an integral of solid angle over a closed surface.
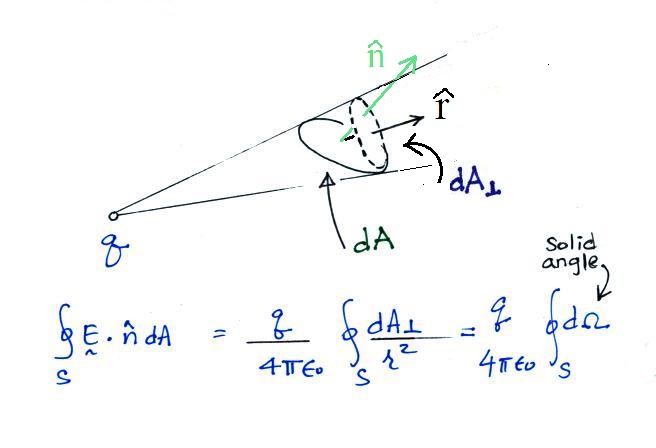
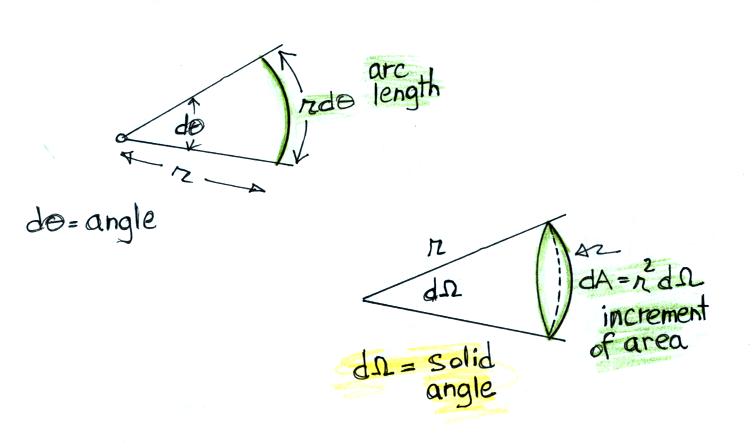
The increment of solid angle
dΩ is really just a 2-dimensional (3-D perhaps because the
distance r is included) version of a 1-dimensional increment
of angle dθ. The following figure might make this clearer.
In the upper figure a line of
length r sweeps through some angle increment dθ (units in
radians) traces out a segment of length rdθ. In the
bottom figure r times an increment of solid angle dΩ (units of
steradians) maps out an area r2
dΩ.
An article in
Wikipedia explains solid angle "is the two-dimensional
angle in three-dimensional space that an object subtends at a
point. It is a measure of how large the object appears to an
observer looking from that point. A small object nearby
may subtend the same solid angle as a larger object farther
away. For example, although the moon is much smaller than the
sun, it is also much closer to earth. Indeed, as viewed from
any point on Earth, both objects have approximately the same
solid angle as well as apparent size. This is evident during a
solar eclipse.
It is relatively easy to show that the integral of solid angle
over a surface is 4 π.
To do this we just consider a
sphere.
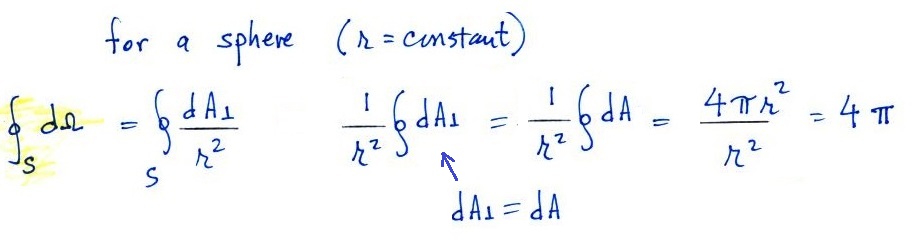
We moved r out of the integral
because it is constant (all points on the surface of the
sphere are the same distance from the center of the
sphere). On the surface of the sphere the normal vector,
n, and the radius vector, r, are parallel. Now let's go
back to the surface integral of the electric field.