Tuesday March 21, 2017

Today we will begin a discussion of lightning return stroke currents.  We'll start by looking at what current properties or parameters are of most interest from a lightning damage/protection point of view.  Return stroke current is now routinely measured in triggered lightning.  Before that measurements of currents were made in strikes to instrumented towers.   We'll look at the kinds of sensors that can be used.   In a future lecture we'll look at how we might determine return stroke currents from remote measurements of lightning electromagnetic fields.

Lightning return stroke "engineering parameters"
Lightning return stroke currents cause different kinds of damage.  Here we'll examine what we need to know about lightning return stroke current characteristics in order to predict the level of damage they may cause and to better be able to design effective lightning protection.

Peak current.  Peak current is of interest when lightning strikes an object that presents a resistive load to the lightning current.  M.A. Uman uses the example of a phase conductor on a power line in his book "The Art and Science of Lightning Protection" (p. 33).  When lightning strikes the line, pulses of current will travel outward away from the strike point much as a signal travels along a long transmission line.  Power lines, apparently, have a characteristic resistive impedance of about 500 ohms.

A 1st return stroke has an average peak current of about 30,000 Amps.  Assume that the current divides in half as it moves away from the strike point as shown above.  This will produce an over-voltage of 15,000 Amps x 500 ohms = 7.5 MVolts in a section of the line.

An electric field of about 3 MV/m breaks down air (at sea level pressure).  A 7.5 MVolt over-voltage thus could be high enough to spark across to a ground wire or to one of the other power lines.  This produces a "fault" and would most likely cause a circuit breaker to trip and stop the flow of current.

Lightning rods on the house sketched below are connected to ground rods that are driven into the soil. 



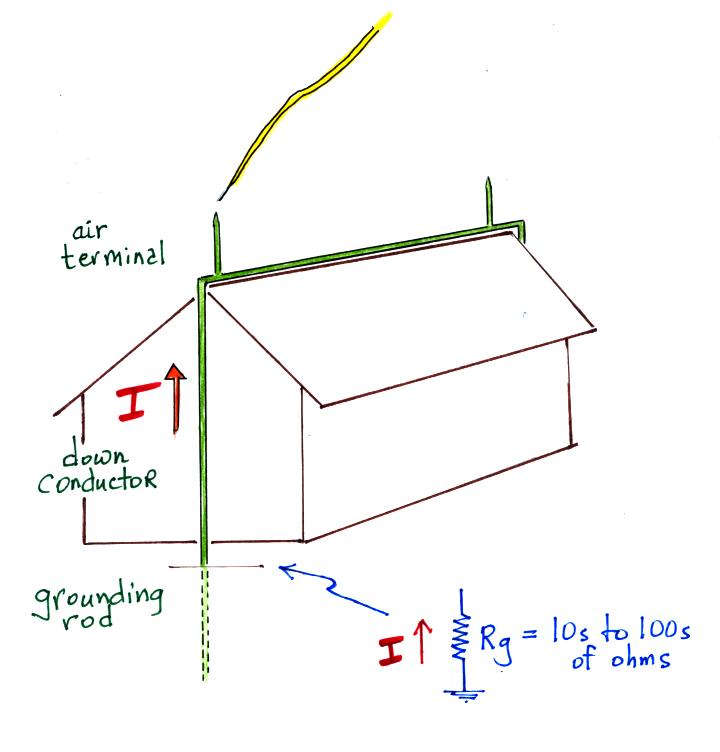
Depending on the soil type and moisture content, the ground resistance can range from a few 10s of ohms to a few 100s of ohms.  A peak current of 30,000 Amps would produce a voltage of 750,000 volts across 25 ohms and 7.5 MVolts across 250 ohms. 

The latter value almost certainly would be enough to spark across to nearby plumbing, electrical wiring, or some other part of the structure .  The lightning rod should be electrically connected (bonded) to nearby water pipe and vent pipes to prevent this kind of occurrence.  When everything is electrically connected, the whole structure would "float" up to 7.5 MVolts, but there wouldn't be any potential differences or arcing through or between different parts of the structure.
Peak dI/dt
The peak value of the return stroke current derivative is of interest if lightning strikes something with an inductive impedance. 

The straight "down conductor" in the sketch above has an impedance, L, of roughly 1 microHenry per meter.  Wires with bends will have higher inductance.  Lightning return strokes (both 1st and subsequent strokes) have peak current derivatives values of about 100 kA/μsec (1011 A/sec).  The voltage produced here will be L x dI/dt = 1011 A/sec x 10-6 H = 100,000 volts for every meter of the down conductor.

Perhaps a more serious problem is that the lightning dI/dt will produce a time-varying magnetic field that can couple into nearby electronics (loops are of primary concern).

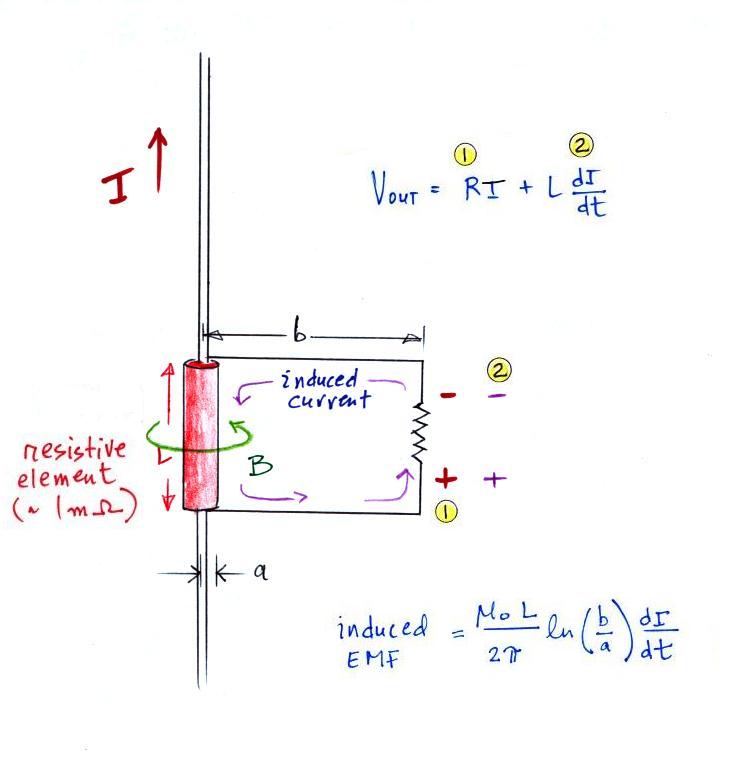
A current moving along a long vertical conductor as shown above will generate an azimuthal magnetic field, B.  Faraday's law of induction states that an electromotive force (EMF) or potential difference (ΔV) will be induced across the open ends of a nearby circuit when the magnetic flux through the crossectional area of the circuit changes with time.  In the simplest case B might be uniform across the area of the circuit.  Then ΔV will just be equal to the area of the circuit times dB/dt.  The time derivative of B in turn depends on the time rate of change of the current, dI/dt.  Large lightning dI/dt values can induce damaging voltages in sensitive electronics.


Q(charge transfer = ∫ I dt)
 The time integral of the return stroke current gives the total charge transferred during the strike.  This apparently determines (and this is something I don't really understand) whether the lightning current will burn through a sheet of metal (such as a metal roof or the thin metal skin of an airplane).


The lightning will burn through the metal sheet unless heat can be carried away from the strike point quickly enough.   Not as much charge would be needed to burn through thin sheets because they won't be able to dissipate heat as quickly as thicker sheets.  Here it is the continuing currents that are of concern because that is where most of the charge transfer occurs.  I like to think of the lightning strike resembling an arc welder in this kind of a situation. 

Action integral ( ∫I2 dt )
The last parameter of interest is called the action integral


The instantaneous power dissipated by a resistive load is


so the energy deposited is R times the action integral

This will cause heating, melting, even vaporization of materials with low electrical conductivity that are struck by lightning.  Lightning can vaporize the sap in a tree, for example, and cause the tree to explode.

Measuring return stroke current
Some of the earliest estimates of return stroke peak currents come from measurements of the residual magnetism in nephelitic basalt (whatever that is) near trees that were struck by lightning (within centimeters of the tree perhaps).  The data were published by Pockels in 1897 & 1898 (the publications would be interesting to look at, but they are in German).

Pockels had determined, in laboratory experiments, that the magnetization of the basalt depended on the peak current value alone and wasn't affected by the shape of the current waveform or its duration. 

The sketch below shows a klydonograph.  A high voltage will produce a Lichtenberg figure on the film. 



The diameter of the pattern depends on the peak voltage which can then be related to peak current if the impedance of the arrangement is known. 



Different patterns are produced depending on the polarity of the applied voltage.  Here's an informative web site with some interesting historical background on Lichtenberg figures.  A Lichtenberg figure like pattern is often burned into the grass on golf courses when lightning strikes the flag on a green.  You'll find a particularly good example from a strike in Tucson here.  The figure below, which shows surface arcing produced by a return stroke triggered in Alabama, gives you some appreciation for why this occurs (from V.A. Rakov, "Parameters of Rocket-Triggered Lightning," available at http://www.lightning.ece.ufl.edu/PDF/Rakov%20%5B2010%5Da.pdf, see also Rakov (2010) in the reference list at the end of these notes).


The subsequent stroke that produced this surface arcing had a peak current of 30 kA; the return stroke channel is outside the field of view of this photograph.

At one time "magnetic links" were used extensively by the electric power industry to estimate peak currents in lightning strikes to power lines.



A magnetizable material is positioned perpendicularly to a straight conductor.  Often two or more links are mounted with different orientations and at different distances from the conductor.  The figure below (a follow up to a question in class) shows how you might be able to determine the peak magnetic field that occurred during a lightning strike.


One end of the link is mounted a known distance, r1, from the conductor.  The link is taken back to the lab after a strike and you determine that the link material was magnetized out a distance r2 from one end.  You know that it takes a certain magnetic field intensity, Bc, to magnetize the link material.  At distances r < r1 + r  the field must have been greater than Bc.  At distances greater than r1 + r2  the field must have been less.  The field must have exactly Bc at r = r1 + r2.  You could then determine the peak current that would be needed to produce Bc at a distance r.

An inexpensive version of a magnetic link was at one time used at the Kennedy Space Center to estimate peak currents in strikes to certain launch facilities.  A strike to a launch tower would probably require time consuming and expensive testing to ensure the facility hadn't been damaged and was still fully operational. 



A loop of prerecorded magnetic tape (on a plastic support and sealed inside a length of  PVC pipe) was positioned perpendicularly to conductors that might carry large amplitude lightning currents.  A portion of the signal on the tape would be erased by the magnetic fields produced by lightning currents.  The magnetic tape wouldn't be removed and analyzed unless the photo bulb had flashed, indicating that a lightning strike had occurred.

A wire loop placed close to a straight conductor (the vertical conductor could be the lightning channel itself) can be used to determine the current derivative.


The output voltage across the open ends of the loop will be proportional to dI/dt.


This is the principle behind a Rogowski Coil used to measure time varying currents moving through a conductor.  Multiple loops of wire on a toroidal support surround the conductor.  The output voltage ΔV will be N times the expression above (N is the number of loops in the Rogowski coil)



The multiple loops of wire increases the inductance which limits the high frequency response of a sensor like this.

A sketch of a faster dI/dt sensor is shown below.


The induced voltage is measured across the gap on the inside surface of the sensor.  Sensors like this are used to measure lightning dI/dt signals and also are used in nuclear electromagnetic pulse testing.

Breaking the current conductor and adding an in-line resistive element is perhaps a more obvious way of measuring lightning currents.

Ideally then you would measure a voltage across the "shunt" that is simply R times I (R is the resistance of the shunt and I is the lightning current).  Very low resistance values (on the order of a milliohm) are needed because peak lightning current amplitudes are large. 

As the picture above shows however, measuring the voltage across the shunt introduces a loop circuit.  The lightning will produce a time varying magnetic field that will couple into the loop.  This will add an L dI/dt term to the output voltage.  Even if L is small, the lightning peak dI/dt can be very large.

The problem with induced voltages in the measuring circuit can be avoided if a coaxial shunt design is used.


Here's a crossectional view.  The resistive element has a cylindrical shape and the measuring circuit is inside the cylinder where the magnetic field is zero (B fields from currents flowing in the right and left hand sides of the cylinder point in opposite directions and cancel).  The measuring instrumentation is placed in the metal enclosure (rectangular or cylindrical), a Faraday cage, at the top part of the figure.  Signals could then be sent out on fiber optics cables to a nearby trailer for recording. Current is shown flowing through one side of the diagram.  In reality it flows through all sides.


There can still be some problems with a coaxial shunt.  Large currents can heat the resistive element and change the resistance (or heat it so much that it is damaged).  Also high frequency currents may only flow through the skin and not through the entire volume of the resistive element and the actual resistance wouldn't be known.



 V.A. Rakov, "Parameters of Rocket-Triggered Lightning," Intl. J. of Plasma Environmental Science & Technology, 4, 80-85, 2010. (available at http://www.lightning.ece.ufl.edu/PDF/Rakov%20%5B2010%5Da.pdf)