Thu., Sep. 11 notes

Each brick weighs 5 pounds. At the bottom of the 5 brick tall pile you would measure a weight of 25 pounds. If you moved up a brick you would measure a weight of 20 pounds, the weight of the four bricks still above. In the atmosphere, pressure at any level is determined by the weight of the air still overhead. Pressure decreases with increasing altitude because there is less and less air remaining overhead. The numbered points on the figure below were added after class.

At sea level altitude, at Point 1, the pressure is normally about 1000 mb. That is determined by the weight of all (100%) of the air in the atmosphere.

Some parts of Tucson, at Point 2, are 3000 feet above sea level (most of the valley is lower than that). At 3000 ft. about 10% of the air is below, 90% is still overhead. It is the weight of the 90% that is still above that determines the atmospheric pressure in Tucson. If 100% of the atmosphere produces a pressure of 1000 mb, then 90% will produce a pressure of 900 mb.

Pressure is typically about 700 mb at the summit of Mt. Lemmon (9000 ft. altitude at Point 3) and 70% of the atmosphere is overhead..

Pressure decreases rapidly with increasing altitude. We will find that pressure changes more slowly if you move horizontally. It is small horizontal changes that cause the wind to blow however.

Point 4 shows a submarine at a depth of about 33 ft. The pressure there is determined by the weight of the air and the weight of the water overhead. Water is much denser and much heavier than air. At 33 ft., the pressure is already twice what it would be at the surface of the ocean.

Now we'll take this a step further and learn that the rate of pressure decrease with increasing altitude depends on the air density.

There is a lot going on in this picture. 1000 mb at Point 1 is a typical value for sea level pressure. The fact that the pressures are equal at the bottoms of both sides of the picture means that the weight of the atmosphere at the bottom of the picture on the left is the same as the weight of the atmosphere at the bottom of the picture at right. The only way this can be true is if there is the same total amount (mass) of air in both cases.

Point 2 - Moving upward from the ground we find that pressure decreases to 900 mb at the level of the dotted line in the picture at left. This is what you expect, pressure decreases with increasing altitude. In the figure at right you need to go a little bit higher for the same 100 mb decrease.

Since there is a 100 mb drop in both the layer at left and in the layer at right, both layers must contain the same amount (mass) of air.

Point 3 - The most rapid rate of pressure decrease with increasing altitude is occurring in the picture at left.

Point 4 - The air in the picture at left is squeezed into a thinner layer than in the picture at right. The air density in the left layer is higher than in the layer at right.

By carefully analyzing this figure we have proved to ourselves that the rate of pressure decrease with altitude is higher in dense air than in lower density air.

This is a fairly subtle but important concept. We will use this concept several times during the semester. In particular we will need this concept to understand why hurricanes can intensify and get as strong as they do.

Newton's Law of Universal Gravitation is an equation that allows you to calculate the gravitational attraction between two objects. We really didn't work through the following figures in class (except for filling in the boxes at the bottom of p. 28 with the English and Metric units for mass and weight). The reason that they have been included on the online notes is that with a little thought you can appreciate and understand why certain variables appear in Newton's Law and why they appear in either the numerator (direct proportionality) or in the denominator (inverse proportionality).

The gravitational attraction between two objects (M and m in the figures) depends first of all on the distance separating the objects. The gravitational force becomes weaker the further away the two objects are from each other. In the bottom picture above and the top figure below we see that the attractive force also depends on the masses of the two objects.

The complete formula is shown in the middle of the page above. G is a constant. On the surface of the earth G, M, and R don't change. The gravitational acceleration, g, is just the quantity [G times M_earth divided by ( R_earth )² ]. To determine the weight (on the earth's surface) of an object with mass m you simply multiply m x g.

Down at the bottom of the page are the Metric and English units of mass and weight. You have probably heard of pounds, grams, and kilograms. You might not have heard of dynes and Newtons. Most people have never heard of slugs.

Here's another page from the photocopied Class Notes that we didn't cover in class. The weight of a person on the earth and the moon is calculated in English and metric units.

The mass of a person would be the same on the earth and on the moon. The weight of a person depends on the person's mass and on the strength of gravity (the acceleration of gravity term, the g variable below).

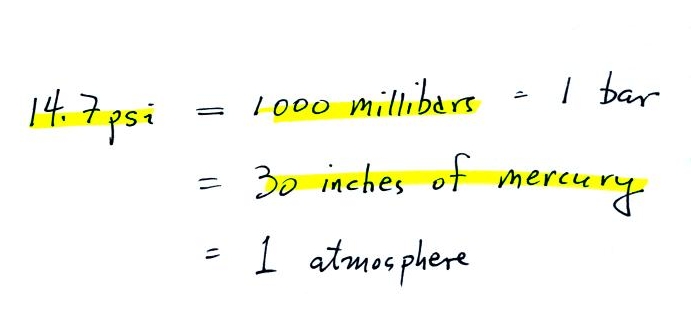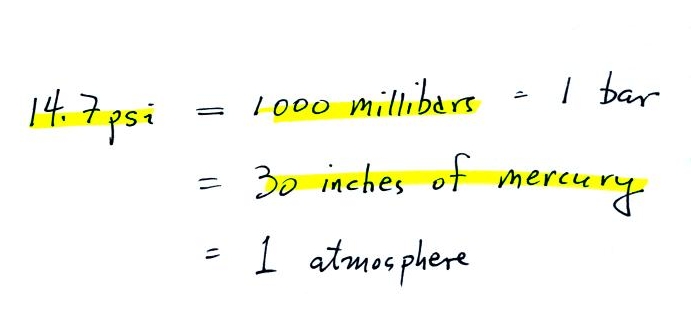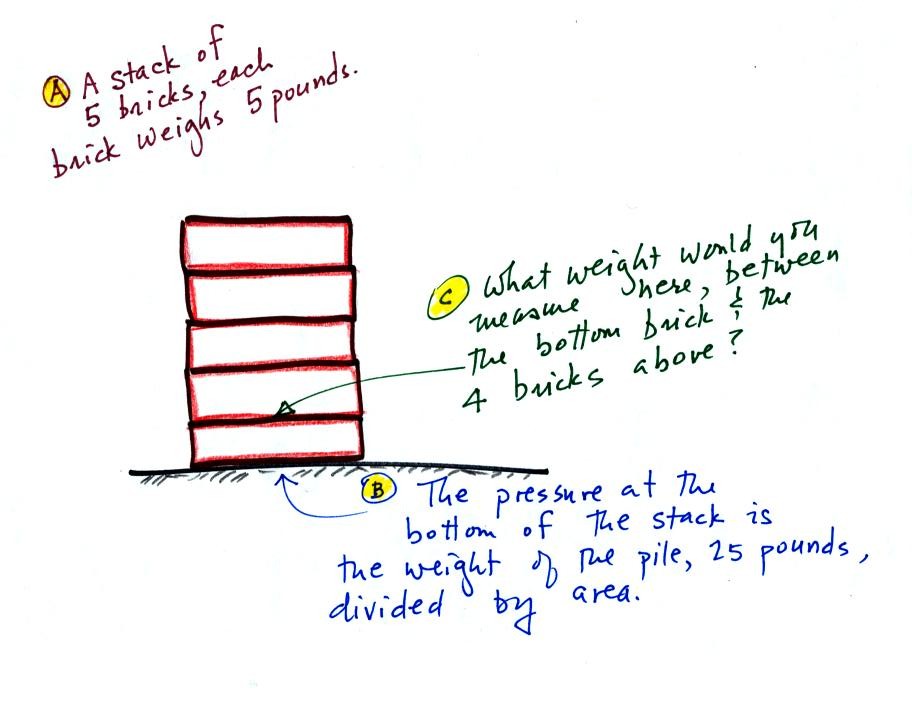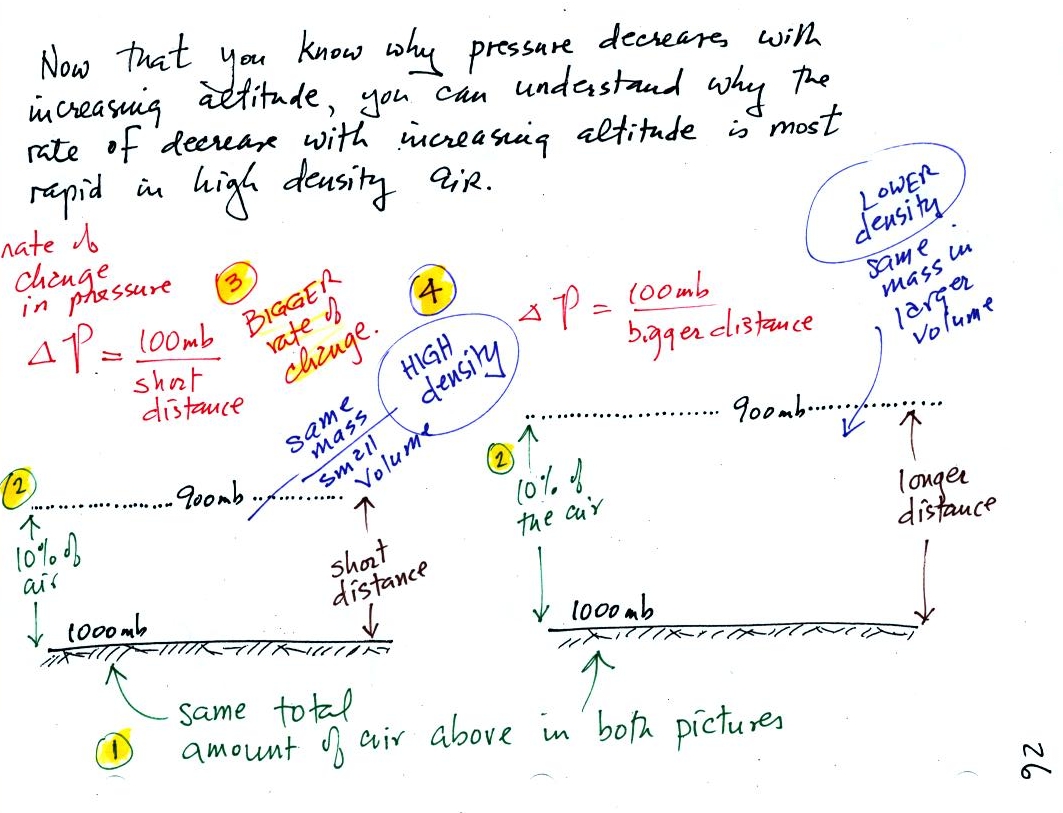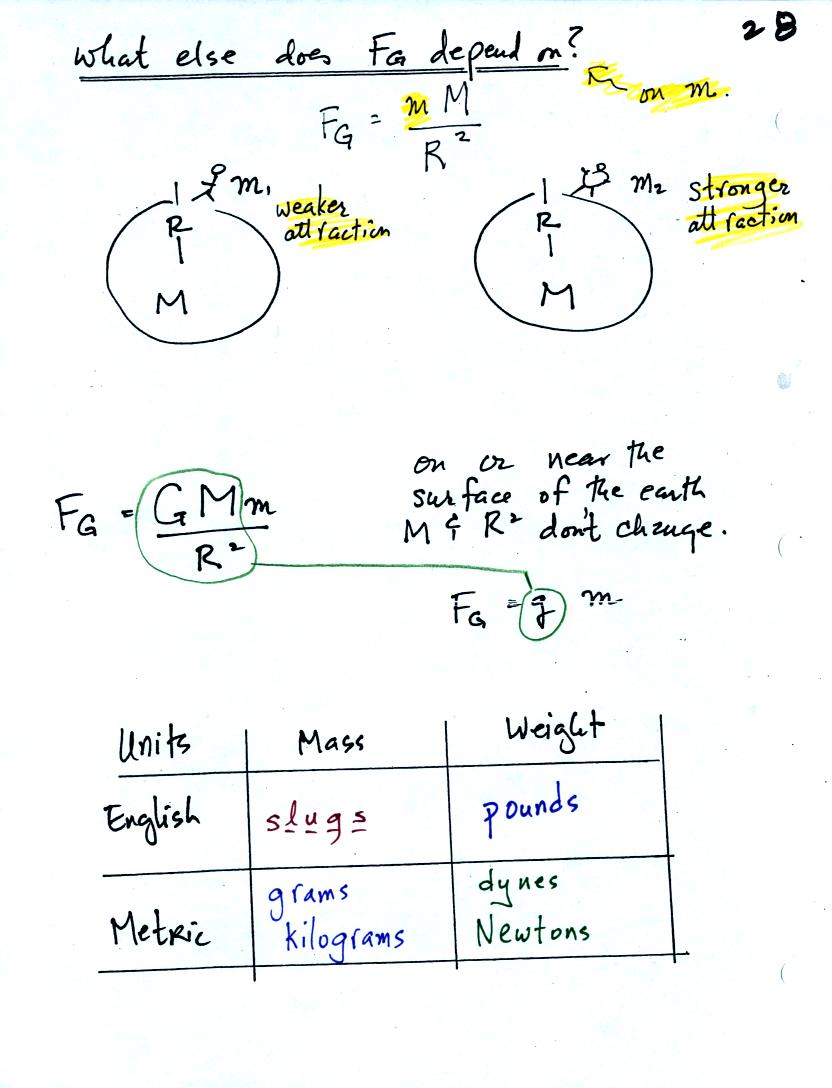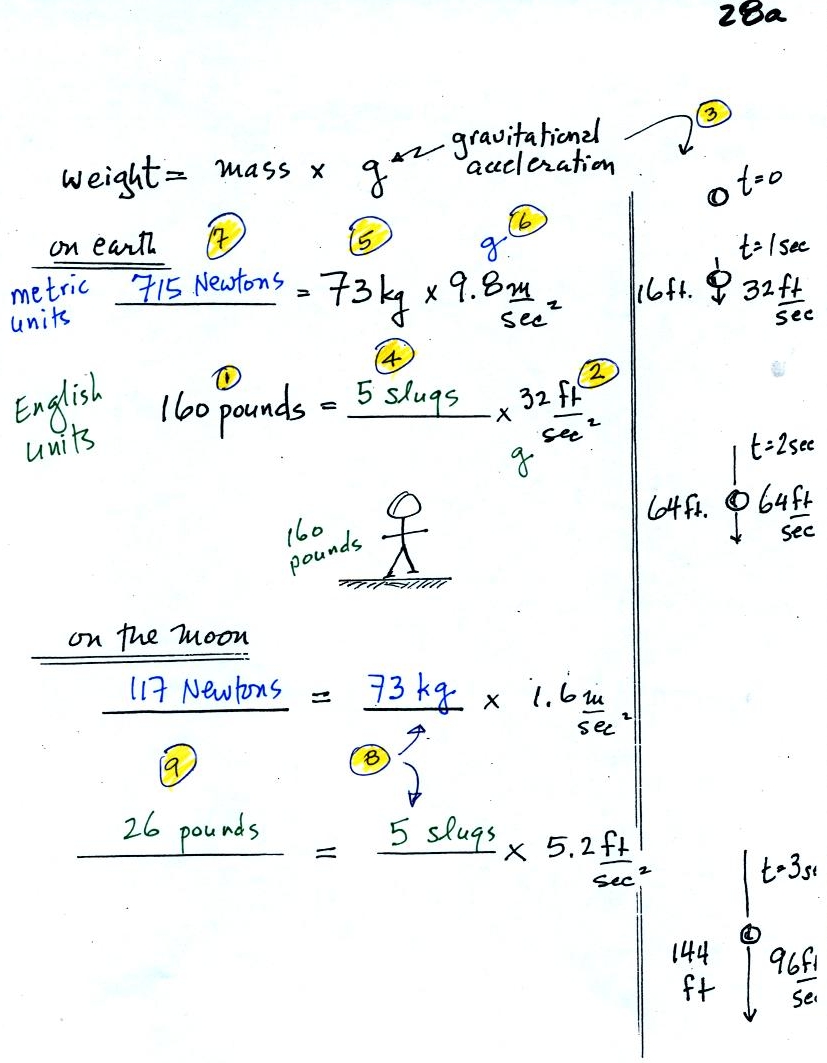
(1) After a long cold winter and without much bicycling or other exercise, the course instructor sometimes weighs as much as 160 pounds. In (2) we see that the gravitational acceleration (g) is 32 ft/sec2 in English units (on the earth). The meaning of this value is shown in (3). If you drop an object it will start to fall and will speed up as it continues to fall. Gravity will cause a falling object to fall 32 ft/sec faster every second. Dividing the instructor's weight by the gravitation acceleration in (4) we obtain the instructor's mass, 5 slugs, in English units.

In metric units, the instructor has a mass of 73 kilograms (5). The gravitation acceleration in metric units is 9.8 m/sec (6). Multiplying these two values, in (7), we find that the instructor weighs 715 Newtons.

On the moon, the mass stays the same. Gravity is weaker, so the value of g is smaller. The instructor would weigh quite a bit less (117 Newtons or 26 pounds) on the moon compared to the earth.

Mercury barometers are used to measure atmospheric pressure. A mercury barometer is really just a balance that can be used to weigh the atmosphere. A basic understanding of how a mercury barometer works is something that every college graduate should have. You'll find most of what follows on p. 29 in the photocopied Class Notes. The figures below are much more carefully drawn versions of what was shown in class.

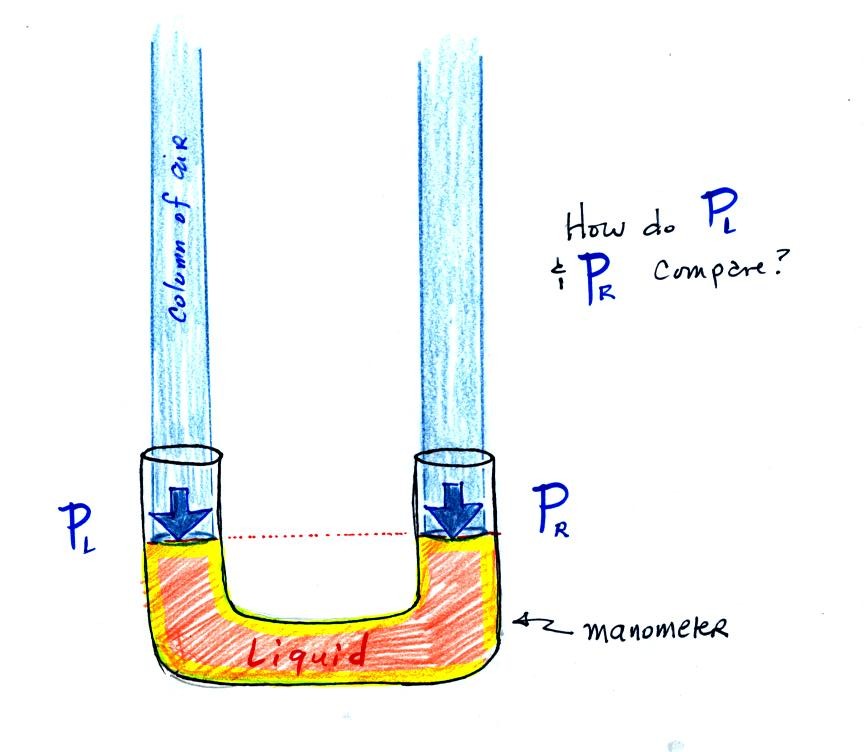
The instrument above ( a u-shaped glass tube filled with a liquid of some kind) is a manometer and can be used to measure pressure difference. The two ends of the tube are open so that air can get inside and air pressure can press on the liquid. Given that the liquid levels on the two sides of the manometer are equal, what could you about P_L and P_R?

The liquid can slosh back and forth just like the pans on a balance can move up and down. A manometer really behaves just like a pan balance.

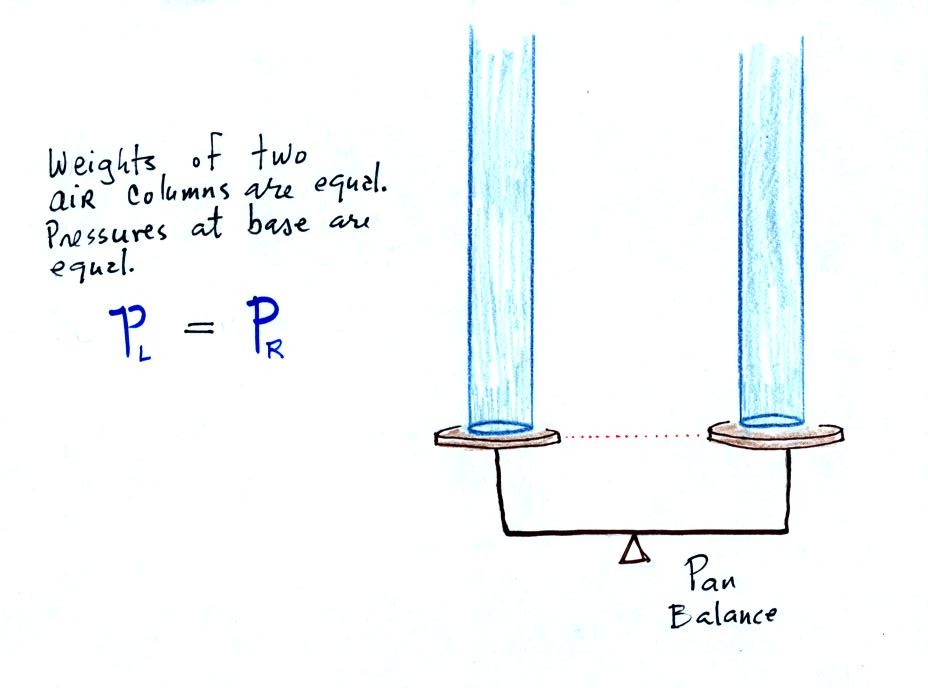
P_L and P_R are equal (note you don't really know what either pressure is just that they are equal).

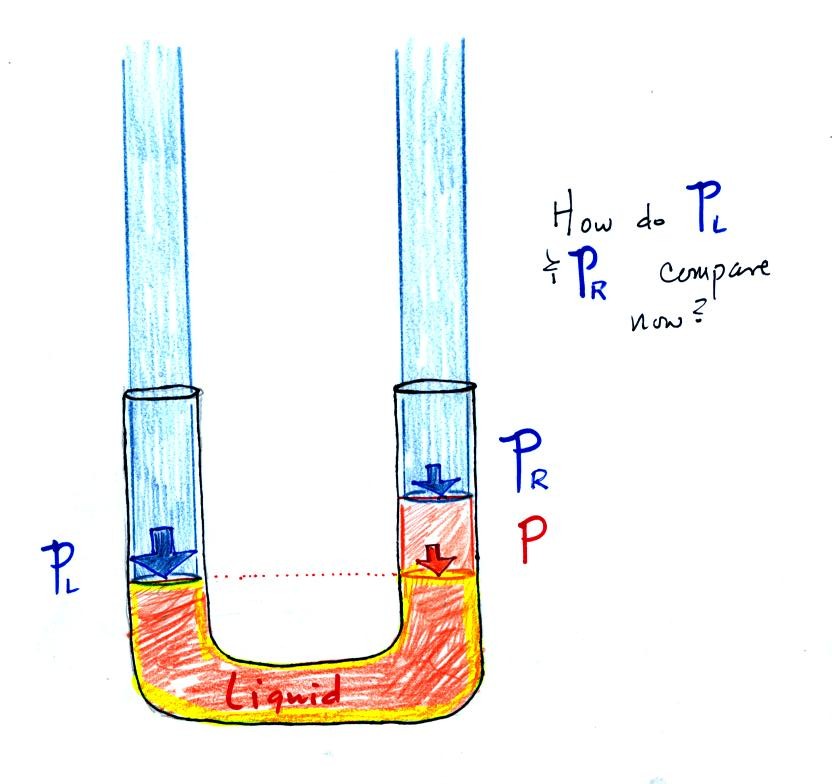
Now the situation is a little different, the liquid levels are no longer equal. You probably realize that the air pressure on the left, P_L, is a little higher than the air pressure on the right, P_R. P_L is now being balanced by P_R + P acting together. P is the pressure produced by the weight of the extra fluid on the right hand side of the manometer (the fluid that lies above the dotted line). The height of the column of extra liquid provides a measure of the difference between P_L and P_R.

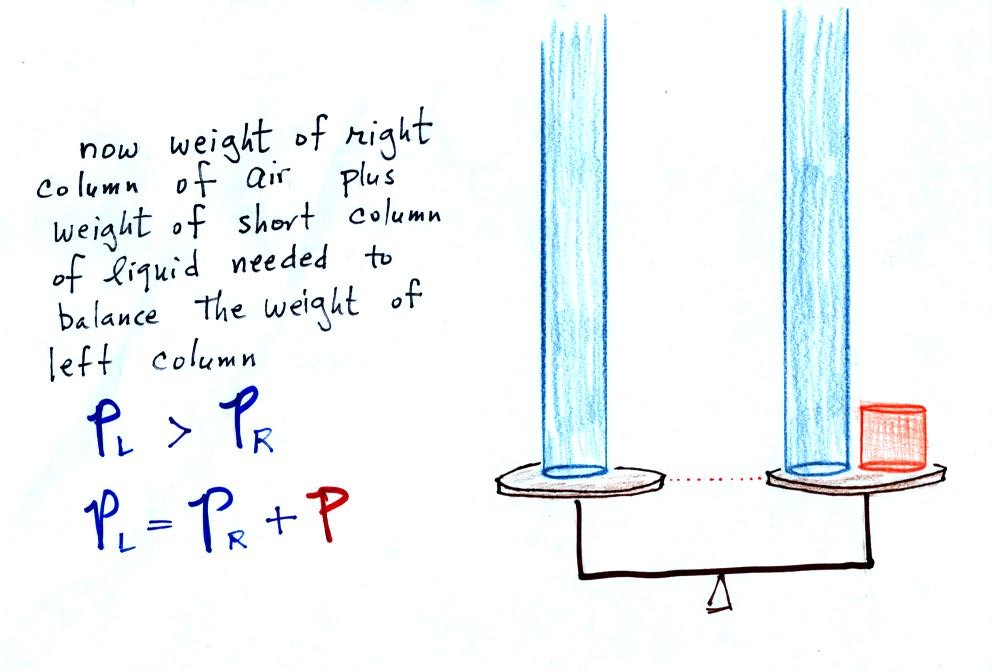
Next we will go an extreme and close off the right hand side of the manometer.

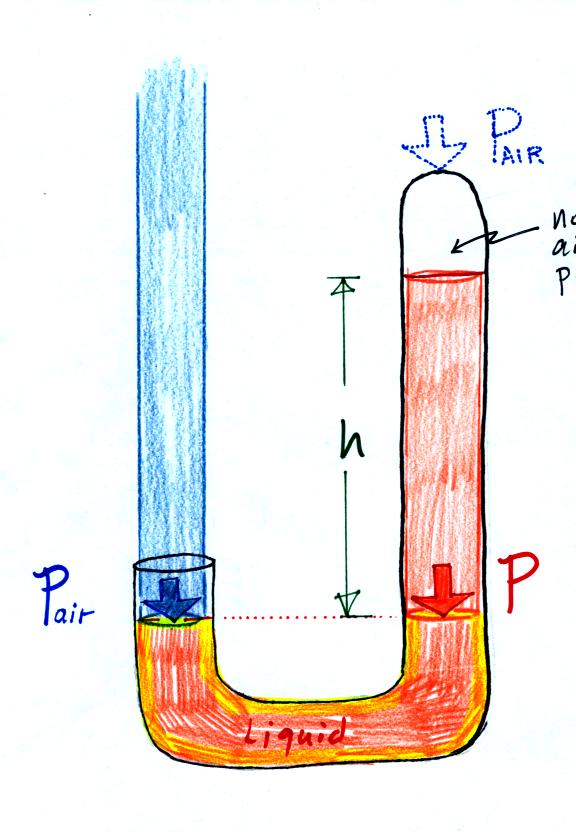
Air pressure can't get into the right tube any more. Now at the level of the dotted line the balance is between P_air and P (pressure by the extra liquid on the right). If P_air changes, the height of the right column, h, will change. You now have a barometer, an instrument that can measure and monitor the atmospheric pressure. (some of the letters were cut off in the upper right portion of the figure, they should read "no air pressure")

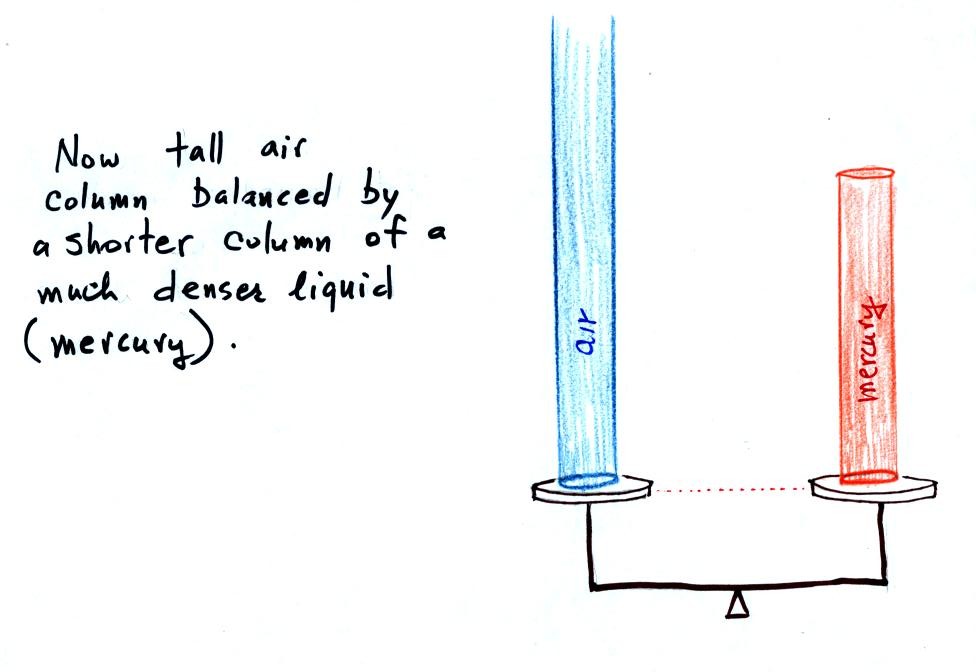
Barometers like this are usually filled with mercury. Mercury is a liquid. You need a liquid that can slosh back and forth in response to changes in air pressure. Mercury is also dense which means the barometer won't need to be as tall as if you used something like water. A water barometer would need to be over 30 feet tall. With mercury you will need only a 30 inch tall column to balance the weight of the atmosphere at sea level under normal conditions (remember the 30 inches of mercury pressure units mentioned earlier). Mercury also has a low rate of evaporation so you don't have much mercury gas at the top of the right tube.

Finally here is a more conventional barometer design. The bowl of mercury is usually covered in such a way that it can sense changes in pressure but not evaporate and fill the room with poisonous mercury vapor.