Monday Oct. 19, 2009
click here to download today's notes in a more printer friendly format

3 songs ( "Wish you Well,"  "Sumatra,"  and "I Will Follow" ) from Katie Hirzog's Apple Tree CD before class today.  She opened the Brandi Carlile concert at The Rialto Theatre last Friday night.

There is a new Optional Assignment due on Wednesday.  There is a new 1S1P Bonus Assignment. Topic #3 is due Friday this week, Topic #4 next week.
We reviewed the introductory material on humidity variables that was stuck onto the end of the Friday Oct. 16 lecture notes.  You are encouraged to read through that material (and look for the hidden optional assignment) if you haven't already done so.

After reading that section, you should be able to say something about each of the four variables shown below (define or explain what they do and give their units)



We spent a little time trying to understand why there is an upper limit to the amount of water vapor that can be found in air and why this depends on the air's temperature.  When air is filled to capacity with water vapor it is saturated and the relative humidity is 100%.

We first must understand the rate at which water evaporates depends on temperature (see p. 84 in the photocopied ClassNotes).  Hot water evaporates more rapidly than cold water.  Wet laundry hung outside on a hot day will dry much more quickly than they would on a cold day.

Before talking about water, have a look at the grade distribution below.  The average appears to be about 77%.  Students with grades equal to or greater than 90.0% are exempt from the final. 

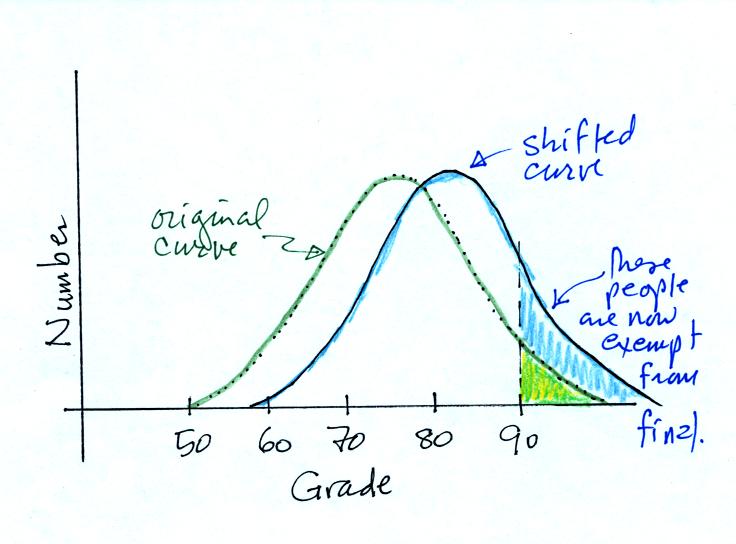
If I added 5 pts to everyones grade,
Would the curve shift to the RIGHT  or the  LEFT?
Would the average grade  INCREASE,  DECREASE  or remain the  SAME?
Would the number of people that don't have to take the final  INCREASE,  DECREASE  or remain the  SAME?

Most everyone understood the curve would shift to the right as shown below.



The average grade would INCREASE and the number of people getting out of the final exam would INCREASE.

The next question was very similar.  Instead of grades, the figure below shows the distribution of the kinetic energies of water molecules in a glass of water.  There's an average and some of the water molecules (the ones at the far right end of the curve) have enough kinetic energy to be able to evaporate (similar to students that are exempt from the final exam).


If the water were heated, would the curve shift to the  RIGHT  or the  LEFT.  Would the average kinetic energy of the water molecules  INCREASE, DECREASE  or  remain the  SAME?.  Would the number of water molecules, with enough kinetic energy to be able to evaporate  INCREASE,  DECREASE,  or remain the  SAME?  The shifted curve is shown below  




The value of the average kinetic energy would increase and more molecules would lie to the right of the threshold and be able to evaporate.  Thus we conclude that hot water evaporates more rapidly than cold water.  This is shown pictorially below (the number of arrows is a measure of the rate of evaporation).







And now a completely different type of question.  The situation is shown below.


It was basically a question about how many people would have to be inside the Walmart in order for the rates at which people enter (10 people per minute) and at which people leave (10% of the people inside leave every minute) to be equal.  Once this balance is reached the number of people inside the store will remain constant.

A student answered the question correctly.  Details are shown below

rate entering = rate leaving

10 people/minute = 10% x (no. of people inside)

solve for (no. of people inside) by dividing both sides of the equation by 10% written in decimal form (0.1)
I.e.   10 / 0.1 = 100 people inside.

The Walmart problem is very similar to saturation of air with water vapor which is shown on p. 85 in the photocopied ClassNotes.



The evaporating water in Picture 1 is analogous to people entering a Walmart store.  The amount of water vapor in the air in the covered glass will begin to increase.  Some fraction of the water vapor molecules will condense (even though they might have just evaporated).  The water vapor concentration will build until the rate of condensation balances evaporation.  The air is saturated at that point.  The water vapor concentration won't increase further.  Saturated air has a relative humidity (RH) of 100%. 

Cups filled with cold and warm water are shown at the bottom of the figure.  Because of different rates of evaporation (slow in cold, rapid in warm water) the water vapor concentrations at saturation are different.  Cold saturated air won't contain as much water vapor as warm saturated air.

We had time to work the first of four example problems.  This way you will learn about the 4 humidity variables (mixing ratio, saturation mixing ratio, relative humidity, and dew point temperature).  You'll see what they do and what can cause their values to change.


Here is the first sample problem that we worked in class.   You might have a hard time unscrambling this if you're seeing it for the first time.  The series of steps that we followed are retraced below:


We're given an air temperature of 90 F and a mixing ratio (r) of 6 g/kg.  We're  supposed to find the relative humidity (RH) and the dew point temperature.

We start by entering the data we were given in the table.  Once you know the air's temperature you can look up the saturation mixing ratio value; it is 30 g/kg for 90 F air.  90 F air could potentially hold 30 grams of water vapor per kilogram of dry air (it actually contains 6 grams per kilogram in this example).  A table of saturation mixing ratio values can be found on p. 86 in the ClassNotes.

Once you know mixing ratio and saturation mixing ratio you can calculate the relative humidity (you divide the mixing ratio by the saturation mixing ratio, 6/30, and multiply the result by 100%).  You ought to be able to work out the ratio 6/30 in your head (6/30 = 1/5 = 0.2).  The RH is 20%. 


The numbers we just figured out are shown on the top line above.

(A) We imagined cooling the air from 90F to 70F, then to 55F, and finally to 45F.

(B) At each step we looked up the saturation mixing ratio and entered it on the chart.  Note that the saturation mixing ratio values decrease as the air is cooling.

(C) The mixing ratio doesn't change as we cool the air.  The only thing that changes r is adding or removing water vapor and we aren't doing either. 

(D) Note how the relative humidity is increasing as we cool the air (Item 6).  The air still contains the same amount of water vapor it is just that the air's capacity is decreasing.

Finally at 45 F the RH becomes 100%.  This is kind of a special point.  You have cooled the air until it has become saturated.  The dew point temperature in this problem is 45 F.

What would happen if we cooled the air further still, below the dew point temperature?


35 F air can't hold the 6 grams of water vapor that 45 F air can.  You can only "fit" 4 grams of water vapor into the 35 F air.  The remaining 2 grams would condense.  If this happened at ground level the ground would get wet with dew.  If it happens above the ground, the water vapor condenses onto small particles in the air and forms fog or a cloud.  Now because water vapor is being taken out of the air (and being turned into water), the mixing ratio will decrease from 6 to 4.

In many ways cooling moist air is liking squeezing a moist sponge (this figure wasn't shown in class)



Squeezing the sponge and reducing its volume is like cooling moist air and reducing the saturation mixing ratio.  At first when you sqeeze the sponge nothing happens, no water drips out.  Eventually you get to a point where the sponge is saturated.  This is like reaching the dew point.  If you squeeze the sponge any further (or cool air below the dew point) water will begin to drip out of the sponge (water vapor will condense from the air).