Friday Oct. 15, 2010
click here
to download today's notes in a more printer friendly format
"No Sugar
Tonight/New Mother Nature" from the Guess Who and "Magic Carpet Ride"
from Steppenwolf seemed like reasonable music at the end of a busy week
in NATS 101.
Experiment #3 materials were
distributed before class today. There are about 10 sets of
materials left. I'll bring them to class on Monday.
Quiz #2 has been graded and was returned in class today.
Question #18 on the quiz (see below) was "thrown out" because it was
clear when grading the quiz that the question was confusing and
students weren't sure how to handle it. An adjustment has been
made in the formula used to determine the percentage grade on the quiz.

Here's what I was thinking

The electric field shows you the direction and gives you an idea of the
strength of the electrical force that would act on a + charge.
The fact that the + charge in Fig. A is moving upward would seem to
indicate that the electric field was pointing in the same
direction. If a - charge in Fig. B is moving downward, then
probably a + charge would move upward (shown in red above). Again
the electric field would point upward.
There was an In-class
Optional
Assignment today. If you download the assignment,
answer the questions, and then turn it in at the start of class on
Monday you can receive at least partial credit for it.
Here's an idea of what we will be covering between now and the next quiz
(with maybe some emphasis on the
items in bold)
humidity, measuring humidity,
heat index
dew and frost, radiation and steam fog
condensation nuclei and cloud
formation
identifying and naming clouds
satellite photographs
precipitation formation and
types of precipitation
The
following is an
introduction to the first item: humidity (moisture in the
air). This topic and the terms that we will be
learning and using can be confusing. That's the reason for this
introduction. We will be mainly be
interested in 4 variables: mixing ratio, saturation mixing ratio,
relative humidity, and dew point temperature. Our first job will
be to figure out what they are and what they're good for. Then we
see what can cause the value of each variable to change. You will
find
much of what follows on page 83 in the photocopied ClassNotes.
Mixing ratio tells you how much water vapor is actually
in
the
air. Mixing ratio has units of grams of water vapor per kilogram
of dry air (the amount of water vapor in grams mixed with a
kilogram
of dry air). It is basically the same
idea as teaspoons of
sugar
mixed in a cup of tea.
The value of the mixing ratio won't change unless you add
water
vapor to or remove water vapor from the air. Warming the air
won't
change the mixing ratio. Cooling the air won't change the mixing
ratio
(one exception is when
the air is
cooled below its dew point temperature and water
vapor starts to condense). Since the mixing ratio's job is to
tell you how much water vapor is in the air, you don't want it to
change unless water vapor is actually added to or removed from the air.

Saturation mixing ratio is just an upper limit
to how much
water vapor
can be found in air, the air's capacity
for water
vapor. It's a
property of air, it doesn't say anything about how much water
vapor is actually in the air (that's the mixing ratio's job).
Warm air can potentially hold
more
water
vapor
than
cold
air.
This variable has the same units: grams of water vapor per kilogram of
dry air. Saturation mixing ratio values for different air
temperatures are listed and graphed on p. 86 in the photocopied class
notes.
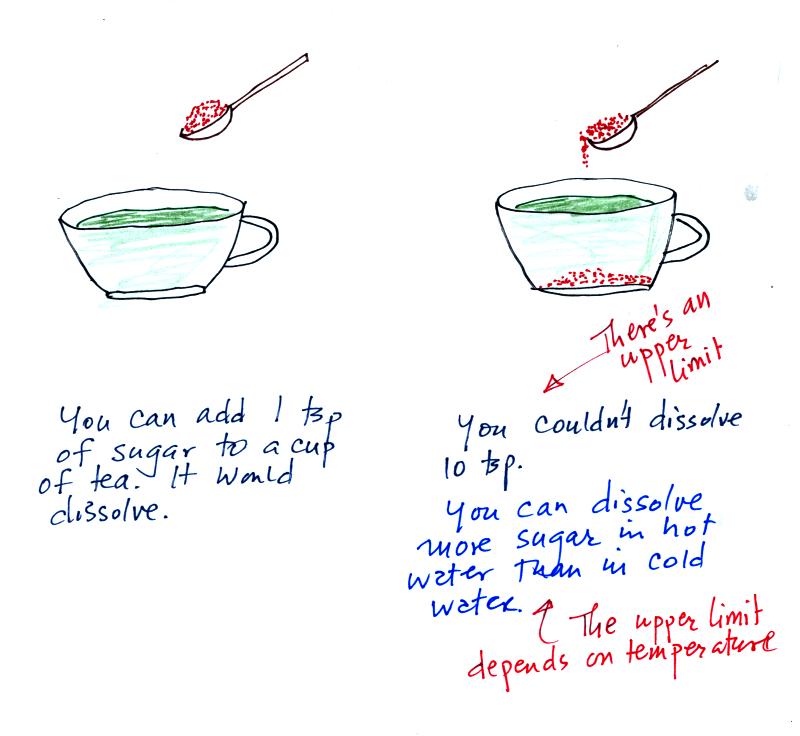
Just as is the case with water vapor in air, there's a limit to
how much sugar can be dissolved in a cup of hot
water. You can dissolve more sugar in hot water
than in cold
water.
The dependence of saturation mixing ratio on air temperature is
illustrated below:
The small specks represent all of the gases in
air except
for the water
vapor. Each of the open circles represents 1 gram of water vapor
that the air could
potentially hold. There are 15 open circles
drawn in the 1
kg of 70 F air; each 1 kg of 70 F air could hold up to 15 grams of
water vapor. The 40 F air only has 5 open circles;
this cooler
air can only hold up to 5 grams of water vapor per kilogram of dry air.
Now we have gone and actually put some water vapor
into the
volumes of
70 F and 40 F air (the open circles are colored in). The same
amount, 3 grams of water vapor, has
been added to each
volume of air. The mixing ratio, r, is 3 g/kg in both cases.
The relative
humidity is the variable most people are familiar with, it tells you
how "full" the air is with water
vapor, how close it is to being
filled to capacity with water vapor.
In the analogy (sketched on the right hand side of p. 83 in
the photocopied notes) 4 students wander into Classroom A which has 16
empty
seats. Classroom A is filled to 25% of its capacity.
You
can
think
of
4,
the
actual
number of students, as being analogous to the
mixing ratio. The classroom capacity is analogous
to the
saturation mixing ratio. The percentage occupancy is analogous to
the relative humidity.
The figure below goes back to the
volumes (1 kg each) of 70 F and 40 F air that could potentially hold 15
grams or 5 grams, respectively of water vapor.

Both the 70 F and the 40 F
air
that each
contain 3 grams of water vapor. The 70 F air is only filled to
20% of capacity (3 of the 15 open circles is colored in) because
this warm air's saturation mixing ratio is large. The RH in the
40 F is 60% even though it has the same actual amount of water vapor
because the 40 F air can't hold as
much water vapor and is closer
to
being saturated.
Something important to note: RH
doesn't really tell you how much water
vapor is
actually in the air. The two volumes of air above contain
the
same amount of water vapor (3 grams per kilogram) but have very
different
relative humidities. You could just as easily have two volumes of
air with the same relative humidities but different actual amounts of
water vapor.

The dew point temperature has two jobs. First it gives you an
idea of
the actual amount of water vapor in the air. In this
respect it
is just like the mixing ratio. If the dew point temperature is
low the air doesn't contain much water vapor. If it is high the
air contains more water vapor.
Second the dew point tells you how
much you must cool the air in order
to cause the RH to increase to 100% (at which point a cloud, or
dew or
frost, or fog would form).
If we cool the 70 F air or the 40 F air to 30 F we would
find that the
saturation mixing ratio would decrease to 3 grams/kilogram. Since
the air actually contains 3 g/kg, the RH of the 30 F air would become
100%. The 30 F air would be saturated, it would be filled to
capacity with water vapor. 30 F is the dew point temperature for
70 F air that contains 3 grams of water vapor per kilogram of dry
air. It is also the dew point temperature for 40 F air that
contains 3 grams of water vapor per kilogram of dry air.Because
both
volumes
of
air
had
the
same
amount of water vapor, they
both
also
have
the
same
dew
point temperature.
Now back to the
student/classroom analogy

The 4 students
move into classrooms of smaller and smaller capacity. The
decreasing capacity of the classrooms is analogous to the
decrease in saturation mixing ratio that occurs when you cool
air. Eventually the students move into a classroom that they just
fill to capacity.
This is analogous to cooling the air to the dew point.
Next we'll try to answer the 2 questions above.
We first must understand the rate at which water evaporates depends on
temperature (see p. 84 in the photocopied ClassNotes). Hot water
evaporates more rapidly than cold water. Wet laundry hung outside
on a hot day will dry much more quickly than it would on a cold day.
Before talking about water, have a look at the
grade distribution below. The average appears to be about
77%. Students with
grades equal to or greater than 90.0% are exempt from the final.
If I added 5 pts to everyones
grade,
Would the curve shift to the RIGHT or the LEFT?
Would the average grade INCREASE, DECREASE or
remain the SAME?
Would the number of people that don't have to take the
final
INCREASE, DECREASE or remain the SAME?
It seemed like most everyone
understood that the curve would shift to the RIGHT, the average grade
would
INCREASE,
and the number of people getting out of the final exam would INCREASE.
The next question is very
similar. Instead of grades,
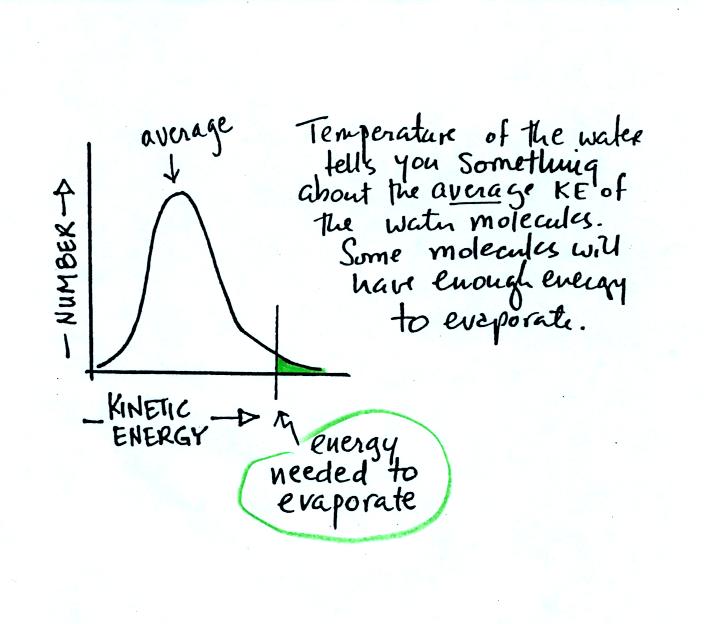
the
figure below shows the distribution of the kinetic energies of
water molecules in a glass of water. There's an average and some
of the water
molecules (the ones at the far right end of the curve) have enough
kinetic energy to be able to evaporate (analogous to students that are
exempt from the final exam). You'll find this figure on p. 84 in
the photocopied ClassNotes.
If the water were heated, would the curve shift to the
RIGHT or the LEFT. Would the average kinetic energy
of the water molecules INCREASE, DECREASE or remain
the SAME?. Would the number of water molecules, with enough
kinetic energy to be able to evaporate INCREASE,
DECREASE, or remain the SAME? The new curve is
shown below
The value of the average kinetic energy would increase and
more
molecules would lie to the right of the threshold and be able to
evaporate. Thus we conclude that hot water evaporates more
rapidly than cold water. This is shown pictorially below (the
number of arrows is a measure of the rate of evaporation).
This
remaining material wasn't covered in class today. We'll
review it quickly on Monday.
And
now a completely different type of question. The situation is
shown below.
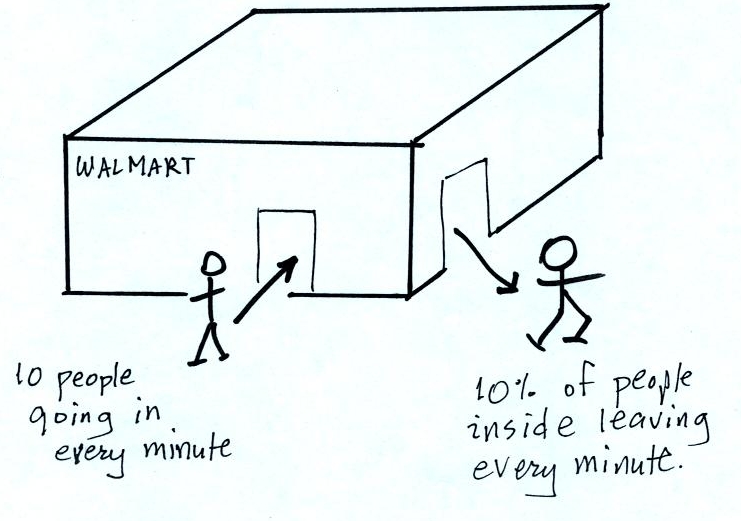
When the front door is first opened people will start streaming
into the Walmart. The number of people in the store will start to
increase. At some point some fraction of the people inside will
start to
leave. Eventually the number inside will grow to the point that
the number of people leaving balances the number entering. The
question is how many people would have to be
inside the Walmart in order for the two rates to be equal?
In the rate of people entering the store were higher, the number
inside would increase. If the rate were to decrease then the
number of people inside would get smaller.
The "Walmart problem" is very similar to saturation of air
with
water vapor which is shown on p. 85 in the photocopied
ClassNotes.

The evaporating water in Picture 1
is analogous to people entering a
Walmart store just as the store opens in the morning. There is
initially no water vapor in the air in the covered glass but it will
begin to buildup (Fig. 2). Some fraction of the water
vapor molecules will condense (even though they might have just
evaporated), this is shown in Fig. 3. The rates of evaporation
and condensation aren't yet equal in Fig. 3 so the water vapor
concentration will increase a little bit more until eventually the
rate of condensation balances evaporation (Fig. 4). The air is
saturated
at that point. The water vapor concentration won't increase
further. Saturated air has a relative humidity (RH) of
100%.
Cups filled with cold and warm water
are shown at the bottom of the figure. Because of different rates
of evaporation (slow in cold, rapid in warm water) the water vapor
concentrations at saturation will be different.
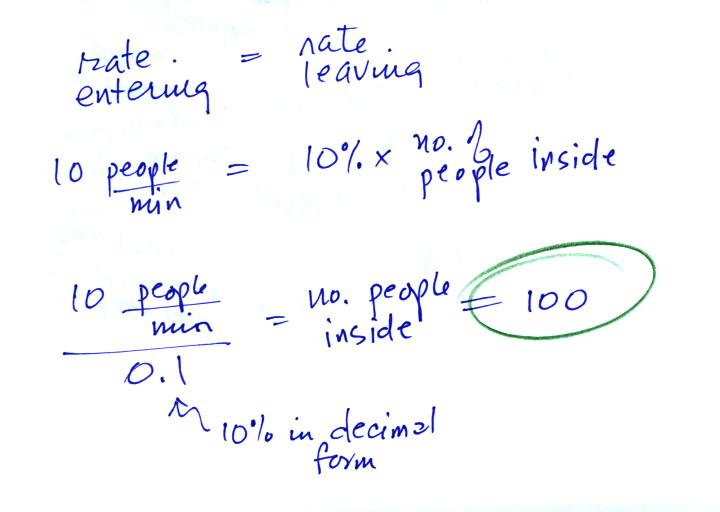
This would be like going back and redoing the Walmart problem assuming
that people were entering the store at different rates: 10
people/minute, 20 people/minute, and 30 people/minute. You'd end
up with 100, 200, and 300 people in the store once the entering and
exiting rates were equal.
One last thing to notice in the bottom part of the figure above.
The relative humidities in the cold and warm cups are the same (100%)
even though the actual amounts of water vapor in the air are very
different. This is proof again that relative humidity really
doesn't tell you how much water vapor is actually in the air. It
only tells you whether the air is full of water vapor or not.