Tuesday Nov. 2, 2010, Election Day
Three Simon and Garfunkel songs before class today ("A Hazy Shade of
Winter", "The
Sparrow", and "American
Tune")
The Experiment #1 revised reports have been graded and were
returned in class today. Experiment #2 revised reports are due
this coming Thursday (unless you've been given extra time).
Many of the Expt. #3 reports were turned in today. Some people
picked up the materials late and have been given extra time. If
you haven't returned your materials please do so as soon as you can.
We covered
the collision-coalescence process in class last Thursday.
It can produce
rain,
drizzle, and
virga (rain that evaporates before reaching the ground), but that's
about it.
Look at what the ice crystal
process can do by contrast. We'll be covering that today.
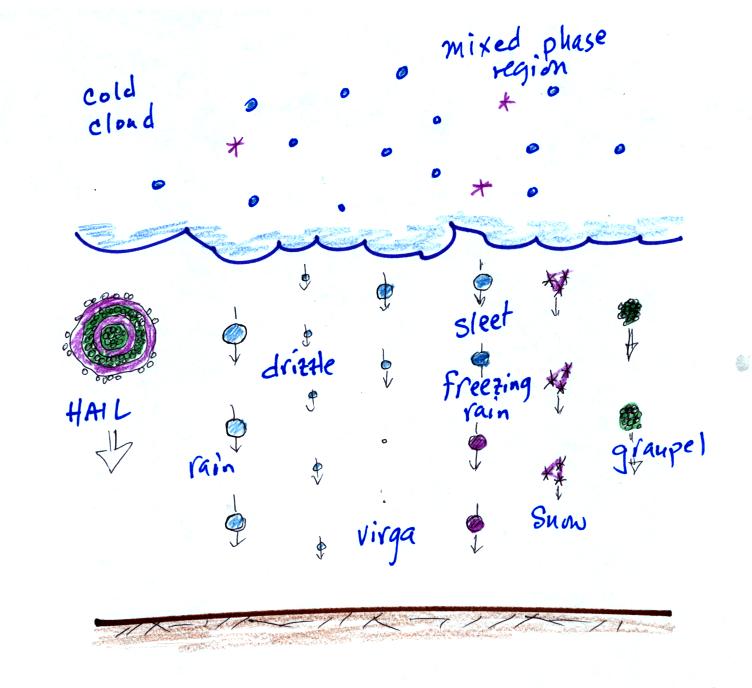
There's
a lot that can happen inside
the cloud and more things that can occur outside the cloud. By
the end of class today you should
know something about every precipitation particle in the picture.
We looked at the structure of cold clouds last Thursday. One
of the important points is that there is a large part of the cloud
where ice crystals and supercooled water droplets are found
together. Today we'll see how ice crystal process works.
There are a couple of
"tricky" parts.
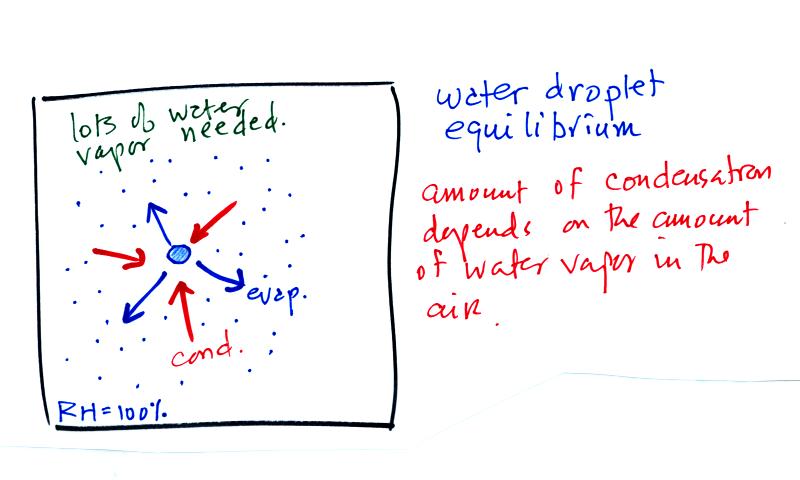
The first figure above (see p.101
in the photocopied
Class
Notes)
shows a water droplet in equilibrium with its surroundings..The droplet
is evaporating (the 3 blue arrows in the figure). The rate of
evaporation will depend on the temperature of the water droplet.
The droplet is surrounded by air that is saturated with water vapor
(the droplet is inside a cloud where the relative humidity is
100%). This means there is enough water vapor to be able to
supply 3 arrows of condensation. Because the droplet loses and
gains water vapor at equal rates it doesn't grow or shrink.
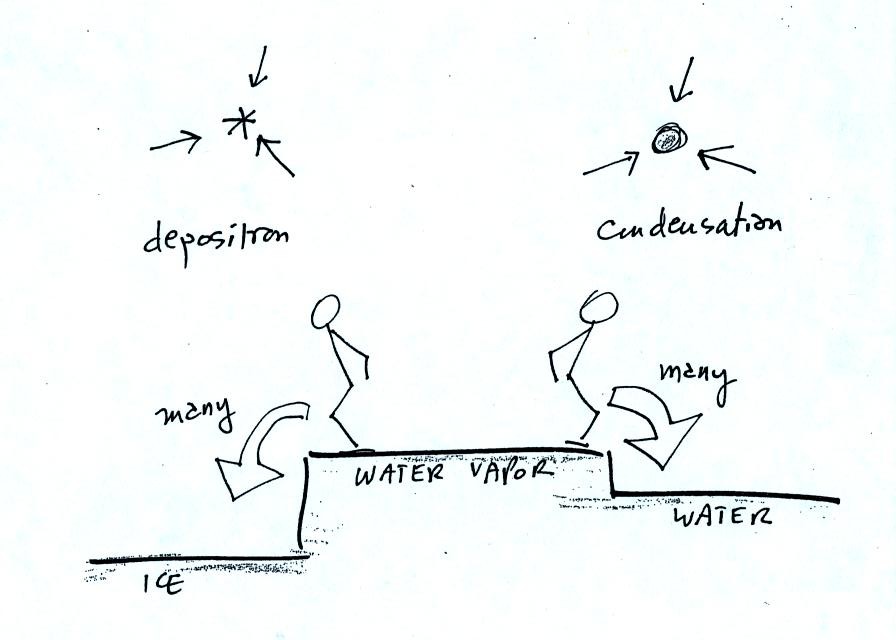
This figure shows what is required
for an ice crystal (at
the same
temperature) to be in equilibrium with its surroundings. First,
the ice crystal won't evaporate as rapidly as the water droplet (only 1
arrow is shown). Going from ice to water vapor is a bigger
jump than going from water to water vapor. There won't be as many
ice molecules with enough energy to make that jump. A sort of
analogous situation is shown in the figure below. The class
instructor could and most of the people in the room could jump from the
floor to the seat of a 12 or 15 inch tall chair. It would be much
tougher to jump to the top of the table (maybe 30 inches off the
ground) or the podium (maybe 36 inches). There wouldn't be as
many people able to do that. Guess what I am going to try to do
this coming weekend in my backyard.
To be in equilibrium the ice crystal only needs 1 arrow of
condensation. There doesn't need to be as much water vapor in the
air surrounding the
ice crystal to supply this lower rate of condensation.

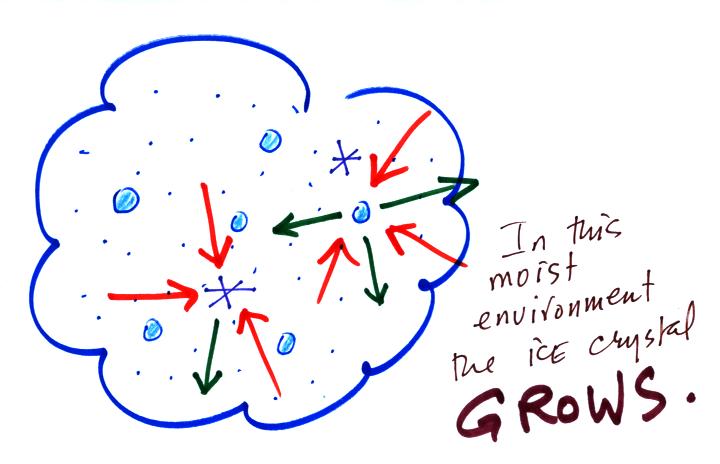
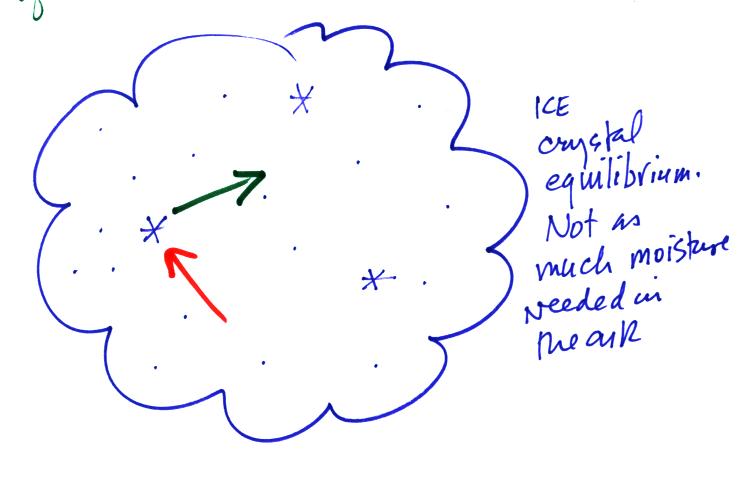
Now what happens in the mixed phase region of a cold cloud
is that
ice crystals find themselves in the very moist surroundings needed for
water droplet equilibrium. This is shown below.
The water droplet is in equilibrium
(3 arrows of evaporation
and 3
arrows of condensation) with the surroundings. The ice crystal is
evaporating more slowly than the water droplet. Because the ice
crystal is in the same surroundings as the water droplet water vapor
will be condensing onto the ice crystal at the same rate as onto the
water droplet. The ice
crystal isn't in equilibrium, condensation
(3 arrows) exceeds evaporation (1 arrow) and the ice crystal will
grow. That's
what makes the ice crystal process work.
The equal rates of condensation are shown in the figure
below using the
earlier analogy.
Most everyone can manage to make the big or the small jump.
Now
we
will
see
what can happen once the ice crystal has had a chance to
grow a little bit.
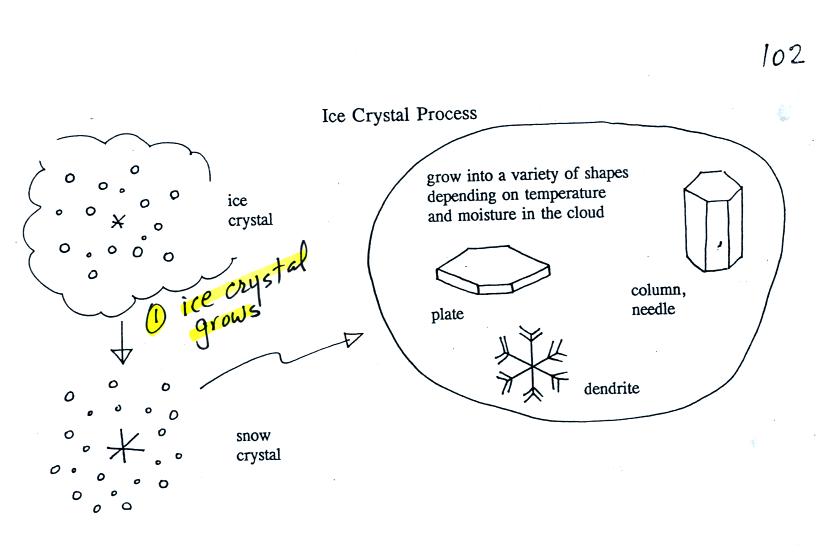
Once an ice
crystal has grown a
little bit it becomes a snow crystal (this figure is on p. 102 in the
photocopied classnotes). Snow crystals can have a variety of
shapes
(plates, dendrites, columns, needles, etc.; these are called crystal
habits) depending on the conditions (temperature and
moisture)
in the cloud. Dendrites are the most common because they form
where there
is the most moisture available for growth. With more raw material
available it makes sense there would be more of this particular snow
crystal
shape.

Here
are some actual photographs of snow crystals (taken with a
microscope). Snow crystals are usually 100 or a few 100s of
micrometers
in diameter (tenths of a millimeter in diameter).
You'll
find some much better photographs and a pile of addtional
information
about snow crystals at www.snowcrystals.com
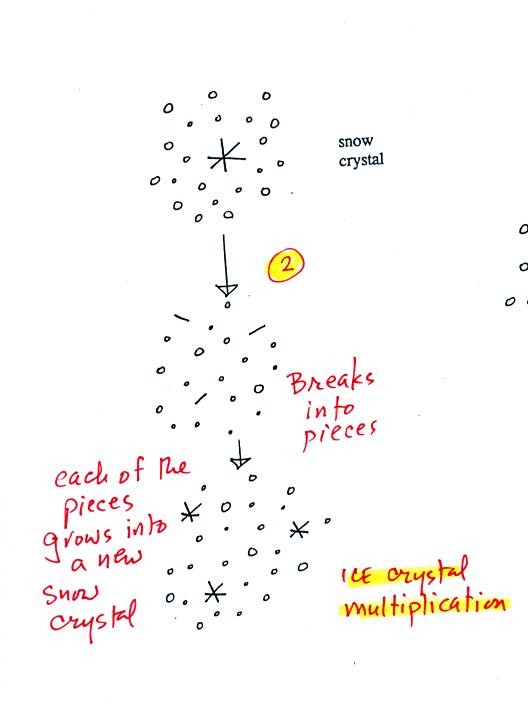
A
variety of things can happen once a snow crystal forms. First it
can
break into pieces, then each of the pieces can grow into a new snow
crystal. Because snow crystals are otherwise in rather short
supply, ice
crystal multiplication is a way of increasing the amount of
precipitation that
ultimately falls from the cloud.
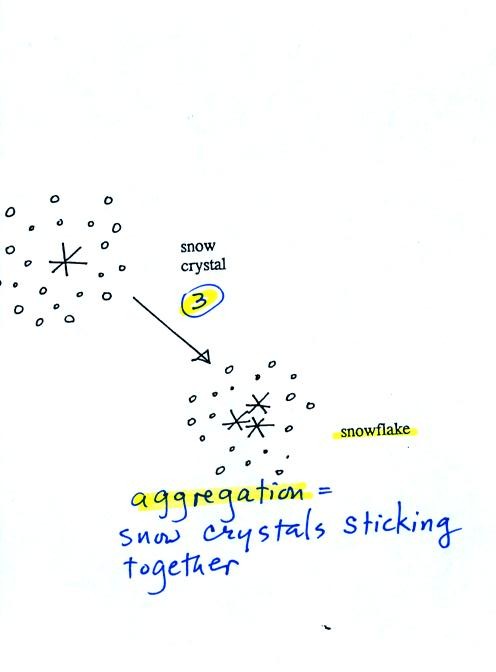
Several
snow
crystals can collide
and stick together to form a snowflake. Snow crystals are small,
a few
tenths of a millimeter across. Snowflakes can be much larger and
are made
up of many snow crystals stuck together. The sticking together or
clumping together of snow crystals is called aggregation (I frequently
forget this term. If I can't
remember it I don't expect you to remember it either)
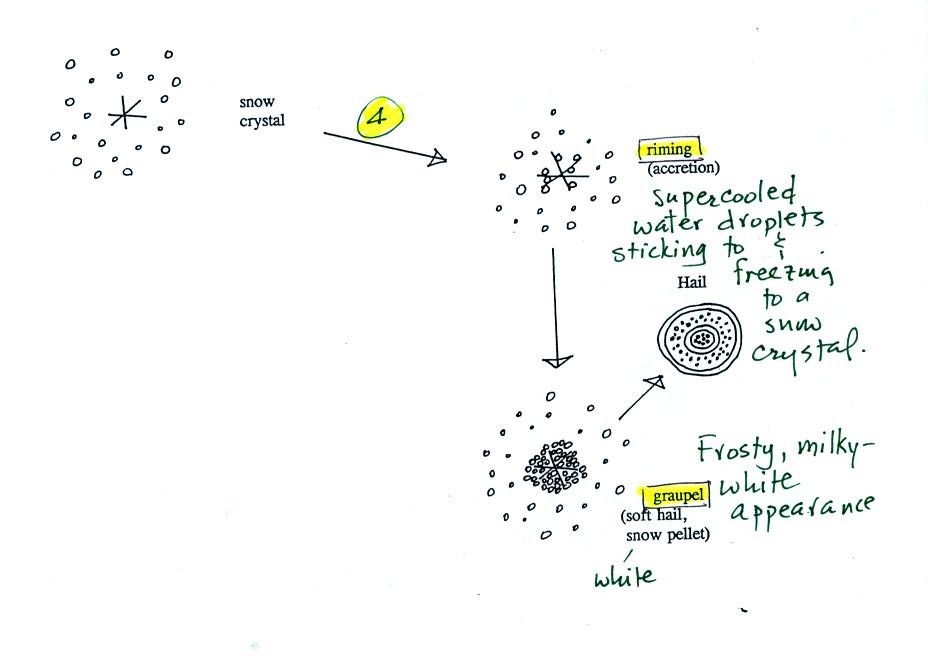
Snow crystals can
collide with supercooled water droplets. The
water
droplets may stick and freeze to the snow crystal. This process
is called
riming or accretion (note this isn't called collision coalescence even
though
it is the same idea). If a snow crystal collides with enough
water
droplets it
can be completely covered with ice. The resulting particle is
called
graupel. Graupel is sometimes mistaken for hail
and is
called soft hail or snow pellets. Rime ice has a frosty milky
white
appearance. A graupel particle resembles a miniature snow
ball.
Graupel particles often serve as the nucleus for a hailstone.
Riming and graupel are terms you should remember.
This figure gives you an idea of
how hail forms.

In the
figure
above a hailstone
starts with a graupel particle (Pt. 1, colored green to represent rime
ice). The
graupel falls or gets carried into a part of the cloud where it
collides with a
large number of supercooled water droplets which stick to the graupel
but don't
immediately freeze. The graupel gets coated with a layer of water
(blue) at Pt. 2. The particle then moves into a colder part of
the cloud
and the
water layer freeze producing a layer of clear ice (the clear ice,
colored
violet, has a distinctly different appearance from the milky white rime
ice), Pt. 3. In Tucson this is often the only example of hail that you
will see:
a graupel particle core with a single layer of clear ice.
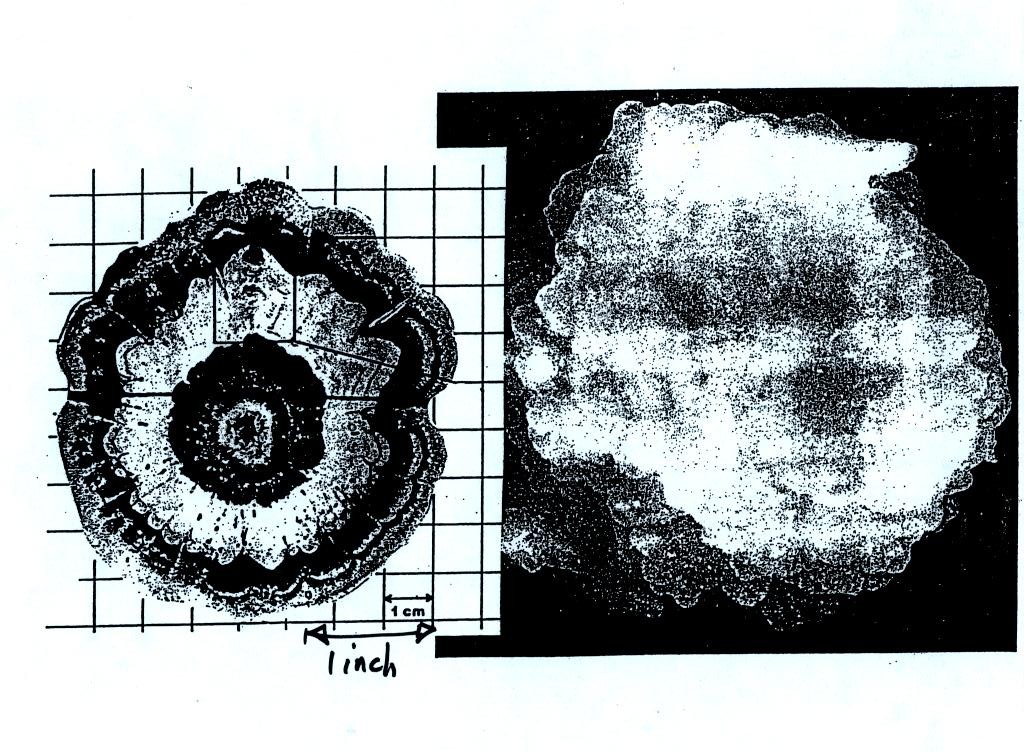
Hail that falls to the ground in Tucson usually just has a graupel core
and a single layer of clear ice. In the severe thunderstorms in
the Central Plains, the hailstone can
pick up additional layers of rime ice and clear ice and hailstones can
be composed
of many
alternating layers of rime and clear ice. An unusually
large
hailstone (around 3 inches in diameter) has been cut in half to show
(below)
the different layers of ice. The picture below is close to actual
size.
Hail is produced
in strong
thunderstorms with tilted updrafts. You would never see hail
(or graupel) falling from a nimbostratus cloud.
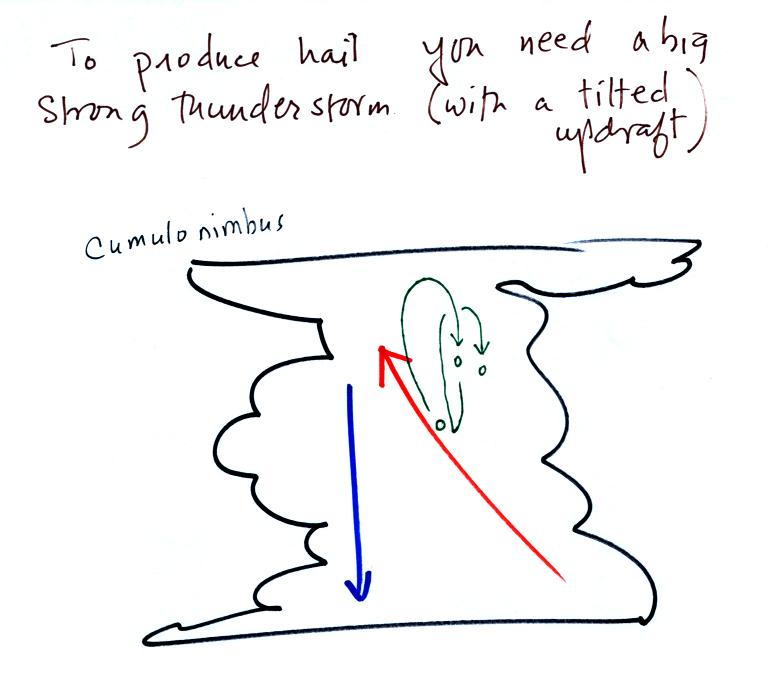
The growing
hailstone can fall
back into the updraft (rather than falling out of the cloud) and be
carried
back up toward the top of the cloud. In this way the hailstone
can
complete several cycles through the interior of the cloud (the motions
are probably more complex than shown here, the hailstone probably moves
horizontally inside the cloud).
One last figure showing some of the
things that can happen once a
precipitation particle falls from a cloud

We'll assume the precipitation
falling from the cloud is either a graupel particle or a snow
flake. Moving from left to right, the falling particles can move
into warmer air and melt. The resulting drops of
water fall the rest of the way to the ground and would be called
RAIN. This is how summer rain in Tucson forms. Note
sometimes the grauple will reach the ground before
melting.
Sometimes the falling raindrops will evaporate before reaching the
ground. This is called VIRGA and is pretty common early in the
summer thunderstorm season in Arizona when the air is still pretty
dry.
Lightning that comes from thunderstorms that aren't producing much
precipitation is called "dry lightning" and often starts brush fires.
Rain will sometimes freeze before reaching the ground. The
resulting particle of clear ice is called SLEET. FREEZING RAIN by
contrast freezes only after it reaches the ground. Everything on
the ground can get coated with a thick layer of ice. It is nearly impossible to
drive
during one of these "ice storms." Sometimes the coating of ice
is heavy enough that branches on trees are broken and power lines are
brought
down. It sometimes takes several days for power to be restored.
Last Friday I gave the students in the MWF section of the class a
chance to submit what they thought might be appropriate questions for
this week's quiz. Click here
to see a sampling of what they came up with.
During the last part of the class we returned to a topic that we
skipped earlier when we were covering humidity variables.
We'll try to answer and understand the 2 questions above.
We first must understand that the rate at which water evaporates
depends on
temperature (see p. 84 in the photocopied ClassNotes). Hot water
evaporates more rapidly than cold water. Wet laundry hung outside
on a hot day will dry much more quickly than it would on a cold day.
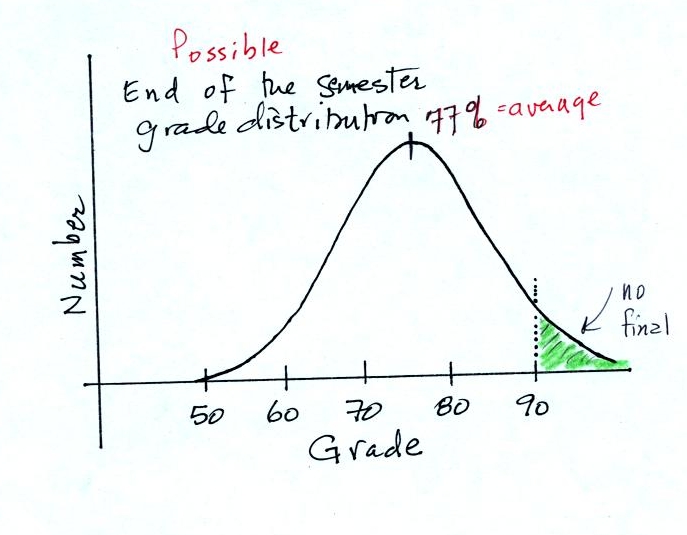
Before talking about water, have a look at the
grade distribution below. The average appears is
77%. Students with
grades equal to or greater than 90.0% are exempt from the final.
If I added 5 pts to everyones
grade,
Would the curve shift to the RIGHT or the LEFT?
Would the average grade INCREASE, DECREASE or
remain the SAME?
Would the number of people that don't have to take the
final
INCREASE, DECREASE or remain the SAME?
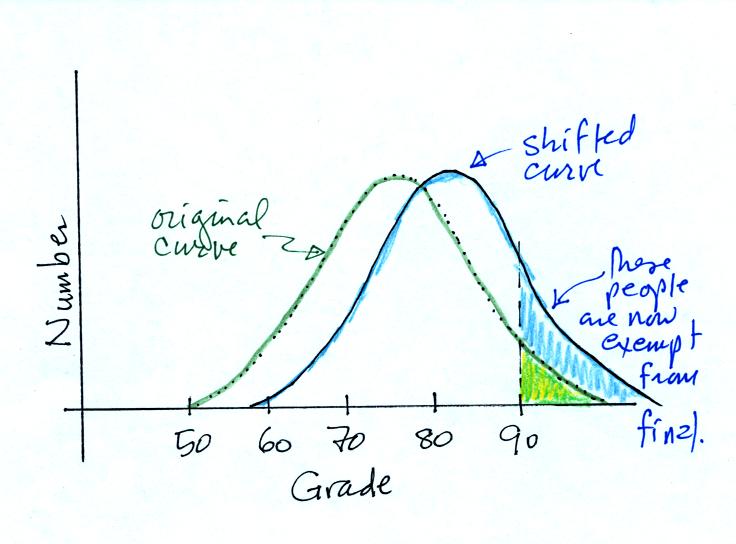
It seemed like most everyone
understood that the curve would shift to the RIGHT, the average grade
would
INCREASE,
and the number of people getting out of the final exam would INCREASE.
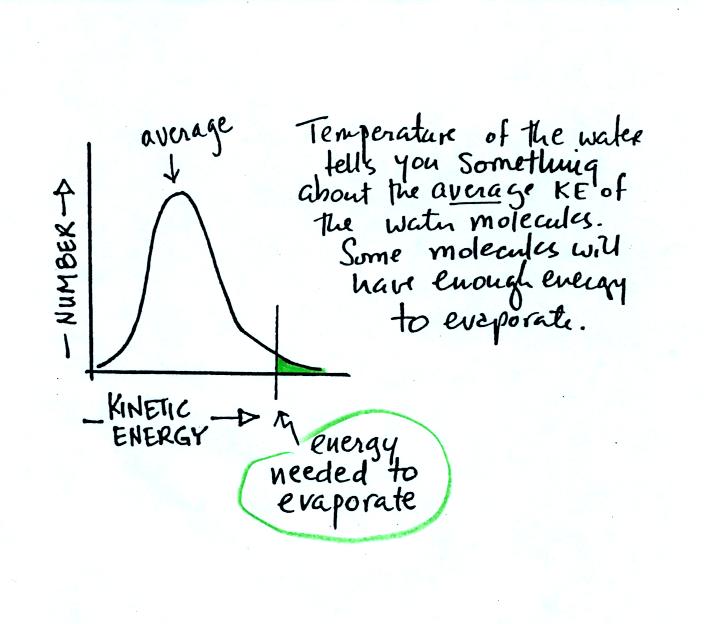
The next question is very
similar. Instead of grades,
the
figure below shows the distribution of the kinetic energies of
water molecules in a glass of water. There's an average and some
of the water
molecules (the ones at the far right end of the curve) have enough
kinetic energy to be able to evaporate (analogous to students that are
exempt from the final exam). You'll find this figure on p. 84 in
the photocopied ClassNotes.
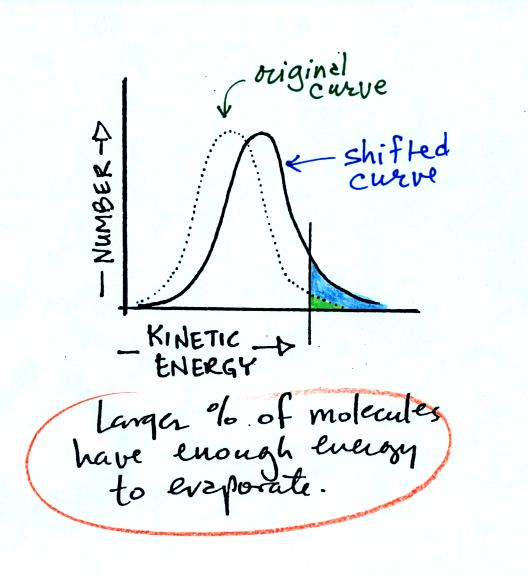
You can ask the same kinds of questions: If the water were heated,
would the curve shift to the
RIGHT or the LEFT. Would the average kinetic energy
of the water molecules INCREASE, DECREASE or remain
the SAME?. Would the number of water molecules, with enough
kinetic energy to be able to evaporate INCREASE,
DECREASE, or remain the SAME? The shifted curve is
shown below
The value of the average kinetic energy would increase and
more
molecules would lie to the right of the threshold and be able to
evaporate. Thus we conclude that hot water evaporates more
rapidly than cold water. This is shown pictorially below (the
number of arrows is a measure of the rate of evaporation).
Next
we'll
try to understand why the rate at which water vapor condenses
depends on the amount of water vapor actually in the air.
Before looking at water vapor we'll consider an analogous situation,
shown below.
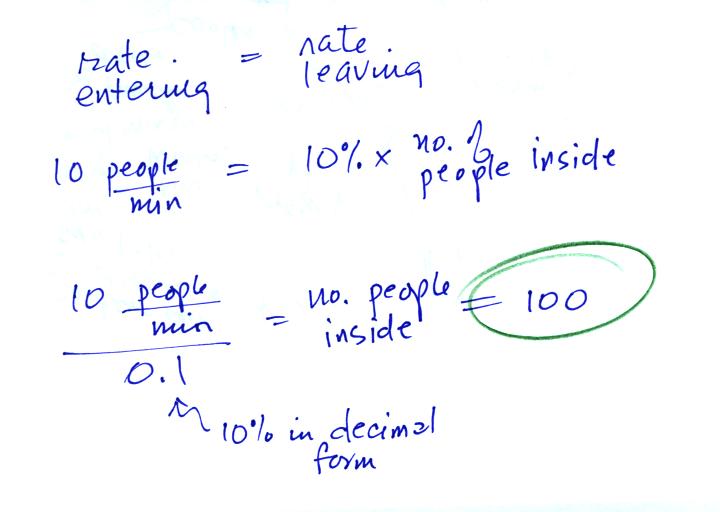
When the front door is first opened people will start streaming
into the Walmart. The number of customers in the store (initially
zero) ill start to
increase. At some point some fraction of the people inside will
start to
leave. Eventually the number inside will grow to the point that
the number of people leaving balances the number entering. The
question is how many people would have to be
inside the Walmart in order for the two rates to be equal?
In the rate of people entering the store were higher (20 people
per minute), the number
inside would increase. If the rate were to decrease then the
number of people inside would get smaller.
The "Walmart problem" is very similar to saturation of air
with
water vapor which is shown on p. 85 in the photocopied
ClassNotes.
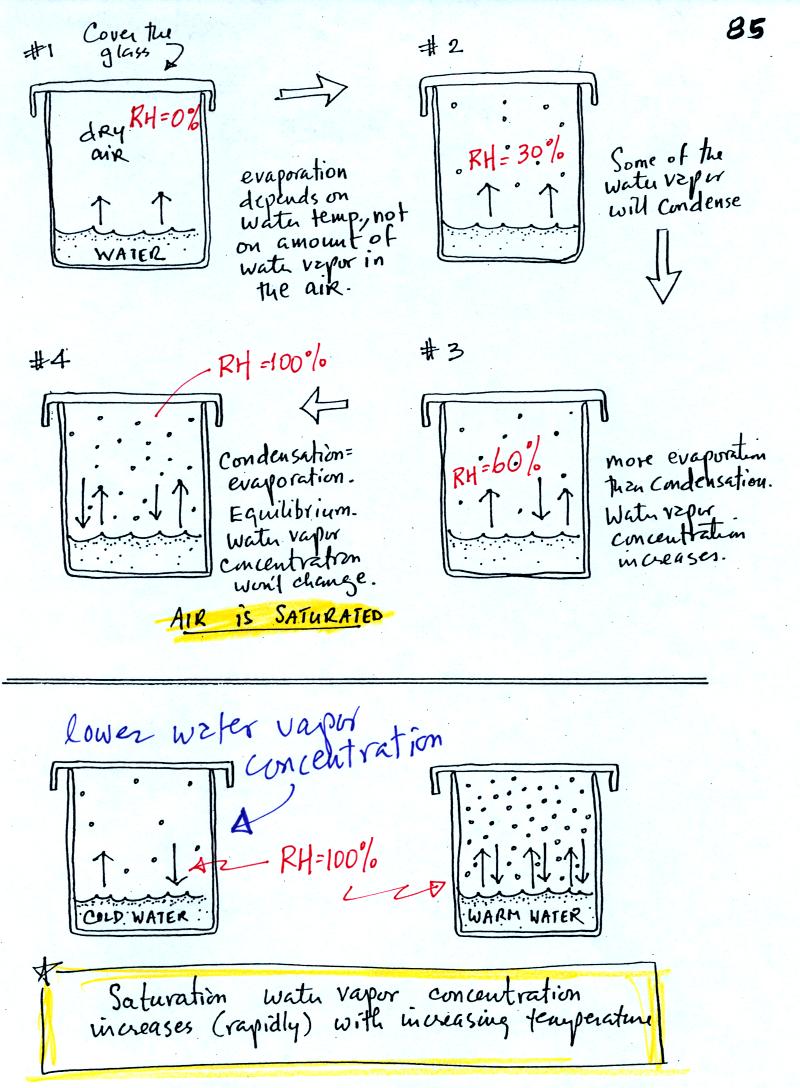
The evaporating water in Picture 1
is analogous to people entering a
Walmart store just as the store opens in the morning. There is
initially no water vapor in the air in the covered glass but it will
begin to buildup (Fig. 2). Some fraction of the water
vapor molecules will condense (even though they might have just
evaporated), this is shown in Fig. 3. The rates of evaporation
and condensation aren't yet equal in Fig. 3 so the water vapor
concentration will increase a little bit more until eventually the
rate of condensation balances evaporation (Fig. 4). The air is
saturated
at that point. The water vapor concentration won't increase
further. Saturated air has a relative humidity (RH) of
100%.
Cups filled with cold and warm water
are shown at the bottom of the figure. Because of different rates
of evaporation (slow in cold, rapid in warm water) the water vapor
concentrations at saturation will be different.
This would be like going back and redoing the Walmart problem assuming
that people were entering the store at different rates: 10
people/minute, 20 people/minute, and 30 people/minute. You'd end
up with 100, 200, and 300 people in the store once the entering and
exiting rates were equal.
One last thing to notice in the bottom part of the figure above.
The relative humidities in the cold and warm cups are the same (100%)
even though the actual amounts of water vapor in the air are very
different. This is proof again that relative humidity really
doesn't tell you how much water vapor is actually in the air. It
only tells you whether the air is full of water vapor or not.
It being
Election Day, we held a vote in NATS 101. The class voted to
postpone starting some new material on Climate Change until later in
the semester.