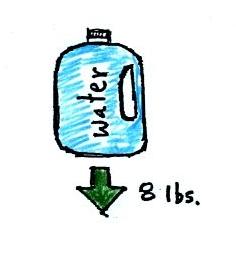Tuesday Sept. 18, 2012
click here to download today's notes in a more printer friendly format

Three songs from The Be Good Tanyas before class this morning.  We started out with "Waiting Around to Die" which is something I heard watching an old episode of Breaking Bad.  That was followed by "Rowdy Blues" and "When Doves Cry".

Both Optional Assignments have been graded and were returned in class today.  If your paper doesn't have a grade it means you earned full credit.  Be sure to check the online answers as not all of the questions are always graded.  Here are answers to Asst. #1 and here are answers to the in-class assignment from last Friday.

Quiz #1 is Thursday this week.  The quiz will cover material on both the Quiz #1 Study Guide and the Practice Quiz Study Guide.  Reviews are scheduled for Tuesday and Wednesday afternoon.  See either study guide for times and locations.

The Experiment #1 reports were collected today.  It takes about 1 week to grade the reports.  If you haven't returned your materials please do so as soon as you can.  The graduated cylinders are used in Experiment #2 and need to be cleaned before they can be checked out.  Experiment #2 materials will be distributed before the quiz on Thursday.

We got a good start on the station model notation last Thursday.  There's one piece of information, pressure, that we need to learn a little more about.


The problem with the pressure number (highlighted in yellow above) is that some information is missing.  Here's what you need to know about the pressure data.


Meteorologists hope to map out small horizontal pressure changes on surface weather maps (that produce wind and storms).  Pressure changes much more quickly when moving in a vertical direction.  The pressure measurements are all corrected to sea level altitude to remove the effects of altitude.  If this were not done large differences in pressure at different cities at different altitudes would completely hide the smaller horizontal changes. 

In the example above, a station pressure value of 927.3 mb was measured in Tucson.  Since Tucson is about 750 meters above sea level, a 75 mb correction is added to the station pressure (1 mb for every 10 meters of altitude).  The sea level pressure estimate for Tucson is 927.3 + 75 = 1002.3 mb.  This sea level pressure estimate is the number that gets plotted on the surface weather map. 

Do you need to remember all the details above and be able to calculate the exact correction needed?  No.  You should remember that a correction for altitude is needed.  And the correction needs to be added to the station pressure.  I.e. the sea-level pressure is higher than the station pressure.

The calculation above is shown in a picture below



Here are some examples of coding and decoding the pressure data. 

First of all we'll take some sea level pressure values and show what needs to be done before the data is plotted on the surface weather map.  These should be the same numbers that we used in class.

To save room, the leading 9 or 10 on the sea level pressure value and the decimal point are removed before plotting the data on the map.  For example the 10 and the decimal pt in 1002.3 mb would be removed; 023 would be plotted on the weather map (to the upper right of the center circle).  Some additional examples are shown above.

You'll mostly have to go the other way - read data off a map and figure out what the sea level pressure is.  This is illustrated below.


When reading pressure values off a map you must remember to add a 9 or 10 and a decimal point.  For example
118 could be either 911.8 or 1011.8 mb. You pick the value that falls  closest to 1000 mb average sea level pressure. (so 1011.8 mb would be the correct value, 911.8 mb would be too low). 

Back to the example from the start of class.  We can now decode the pressure information.



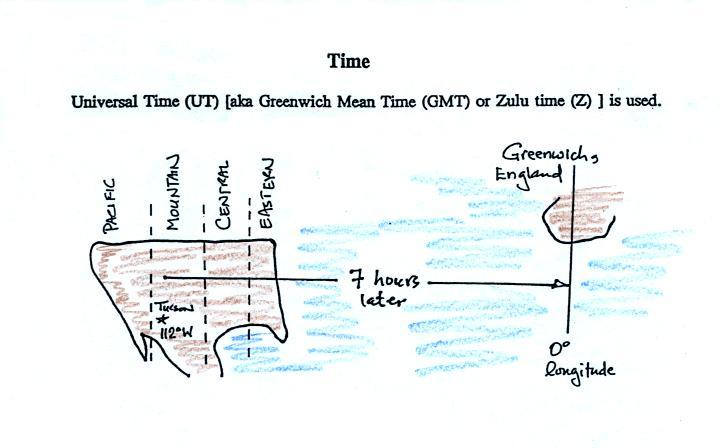
Another important piece of information on a surface map is the time the observations were collected.  We didn't have time for this in class.  Time on a surface map is converted to a universally agreed upon time zone called Universal Time (or Greenwich Mean Time, or Zulu time).  That is the time at 0 degrees longitude, the Prime Meridian. There is a 7 hour time zone difference between Tucson and Universal Time (this never changes because Tucson stays on Mountain Standard Time year round).  You must add 7 hours to the time in Tucson to obtain Universal Time.

Here are several examples of conversions between MST and UT

to convert from MST (Mountain Standard Time) to UT (Universal Time)
10:20 am MST:
add the 7 hour time zone correction --->   10:20 + 7:00 = 17:20 UT (5:20 pm in Greenwich)

2:45 pm MST :
first convert to the 24 hour clock by adding 12 hours   2:45 pm MST + 12:00 = 14:45 MST
add the 7 hour time zone correction --->  14:45 + 7:00 = 21:45 UT (7:45 pm in England)

7:45 pm MST:
convert to the 24 hour clock by adding 12 hours   7:45 pm MST + 12:00 = 19:45 MST
add the 7 hour time zone correction ---> 19:45 + 7:00 = 26:45 UT
since this is greater than 24:00 (past midnight) we'll subtract 24 hours   26:45 UT - 24:00 = 02:45 am the next day

to convert from UT to MST
18Z:
subtract the 7 hour time zone correction ---> 18:00 - 7:00 = 11:00 am MST

02Z:
if we subtract the 7 hour time zone correction we will get a negative number. 
So we will first add 24:00 to 02:00 UT then subtract 7 hours   02:00 + 24:00 = 26:00
26:00 - 7:00 = 19:00 MST on the previous day
2 hours past midnight in Greenwich is 7 pm the previous day in Tucson


A bunch of weather data has been plotted (using the station model notation) on a surface weather map in the figure below (p. 38 in the ClassNotes). 



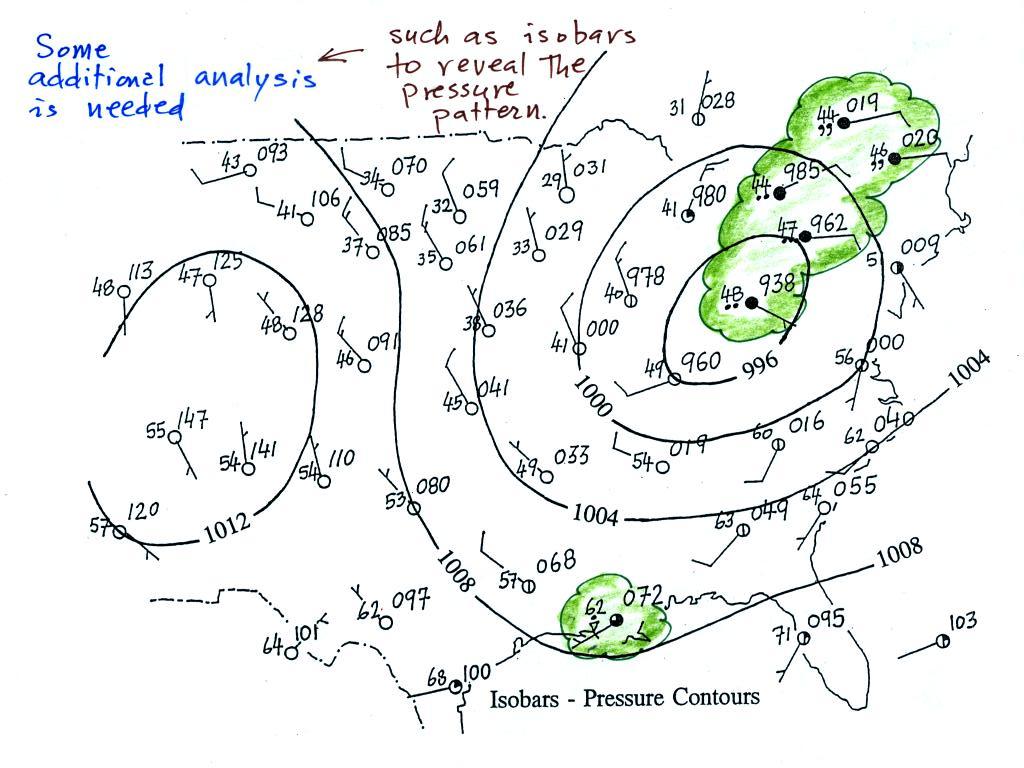
Plotting the surface weather data on a map is just the beginning.  For example you really can't tell what is causing the cloudy weather with rain (the dot symbols are rain) and drizzle (the comma symbols) in the NE portion of the map above or the rain shower along the Gulf Coast.  Some additional analysis is needed.  A meteorologist would usually begin by drawing some contour lines of pressure (isobars) to map out the large scale pressure pattern.  We will look first at contour lines of temperature, they are a little easier to understand (the plotted data is easier to decode and temperature varies across the country in a more predictable way).


Isotherms, temperature contour lines, are usually drawn at 10o F intervals. They do two things: (1) connect points on the map that all have the same temperature, and (2) separate regions that are warmer than a particular temperature from regions that are colder.  The 40o F isotherm above passes through a city which is reporting a temperature of exactly 40o (Point A).  Mostly it goes between pairs of cities: one with a temperature warmer than 40o (41o at Point B) and the other colder than 40o (38o F at Point C).  Temperatures generally decrease with increasing latitude: warmest temperatures are usually in the south, colder temperatures in the north.


Now the same data with isobars drawn in.  Again they separate regions with pressure higher than a particular value from regions with pressures lower than that value.    The isobars also enclose areas of high pressure and low pressure.  Isobars are generally drawn at 4 mb intervals (starting with a base value of 1000 mb).  Isobars also connect points on the map with the same pressure.  The 1008 mb isobar (highlighted in yellow) passes through a city at Point A where the pressure is exactly 1008.0 mb.  Most of the time the isobar will pass between two cities.  The 1008 mb isobar passes between cities with pressures of 1009.7 mb at Point B and 1006.8 mb at Point C.  You would expect to find 1008 mb somewhere in between those two cites, that is where the 1008 mb isobar goes.

The pressure pattern is not as predictable as the isotherm map.  Low pressure is found on the eastern half of this map and high pressure in the west.  The pattern could just as easily have been reversed.

This site (from the American Meteorological Society) first shows surface weather observations by themselves (plotted using the station model notation) and then an analysis of the surface data like what we've just looked at.  There are links below each of the maps that will show you current surface weather data.

Here's a little practice (this figure wasn't shown in class).


Is this the 1000, 1002, 1004, 1006, or 1008 mb isobar? (you'll find the answer at the end of today's notes)

Now we'll look at what you can learn about the weather once you've drawn in some isobars and mapped out the pressure pattern.

1.
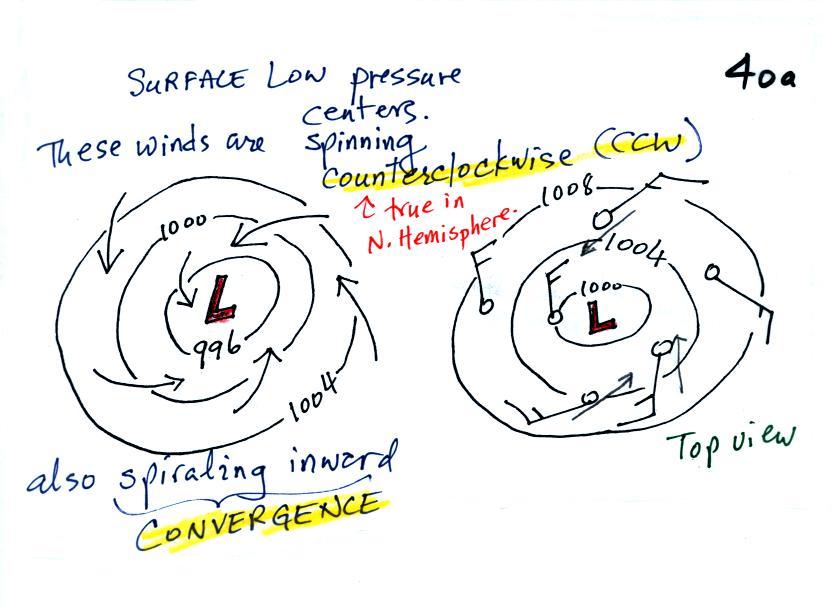
We'll start with the large nearly circular centers of High and Low pressure.  Low pressure is drawn below.  These figures are more neatly drawn versions of what we did in class.



Air will start moving toward low pressure (like a rock sitting on a hillside that starts to roll downhill), then something called the Coriolis force will cause the wind to start to spin (we'll learn more about the Coriolis force later in the semester). In the northern hemisphere winds spin in a counterclockwise (CCW) direction around surface low pressure centers.  The winds also spiral inward toward the center of the low, this is called convergence.  [winds spin clockwise around low pressure centers in the southern hemisphere but still spiral inward, don't worry about the southern hemisphere until later in the semester]


When the converging air reaches the center of the low it starts to rise.  Rising air expands (because it is moving into lower pressure surroundings at higher altitude), the expansion causes it to cool.  If the air is moist and it is cooled enough (to or below the dew point temperature) clouds will form and may then begin to rain or snow.  Convergence is 1 of 4 ways of causing air to rise (we'll learn what the rest are soon, and, actually, you already know what one of them is - warm air rises, that's called convection).  You often see cloudy skies and stormy weather associated with surface low pressure.

Everything is pretty much the exact opposite in the case of surface high pressure.


Winds spin clockwise (counterclockwise in the southern hemisphere) and spiral outward.  The outward motion is called divergence.

Air sinks in the center of surface high pressure to replace the diverging air.  The sinking air is compressed and warms.  This keeps clouds from forming so clear skies are normally found with high pressure.

Clear skies doesn't necessarily mean warm weather, strong surface high pressure often forms when the air is very cold. 

Here's a picture summarizing what we've learned so far.  It's a slightly different view of wind motions around surface highs and low and wasn't shown in class.




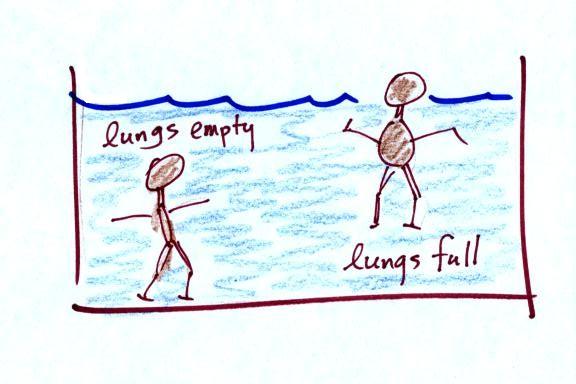
Here's another way of trying to understand why warm air rises and cold air sinks - Archimedes Law.  It's a perhaps simpler way of understanding the topics.  A bottle of water can help you to visualize the law.


A gallon of water weighs about 8 pounds (lbs).  I would want to carry a gallon of water on a hike unless I really thought I would need it.

If you submerge the gallon jug of water in a swimming pool, the jug becomes, for all intents and purposes, weightless.  That seems kind of amazing.  Archimedes' Law (see figure below, from p. 53a in the photocopied ClassNotes) explains why this is true.

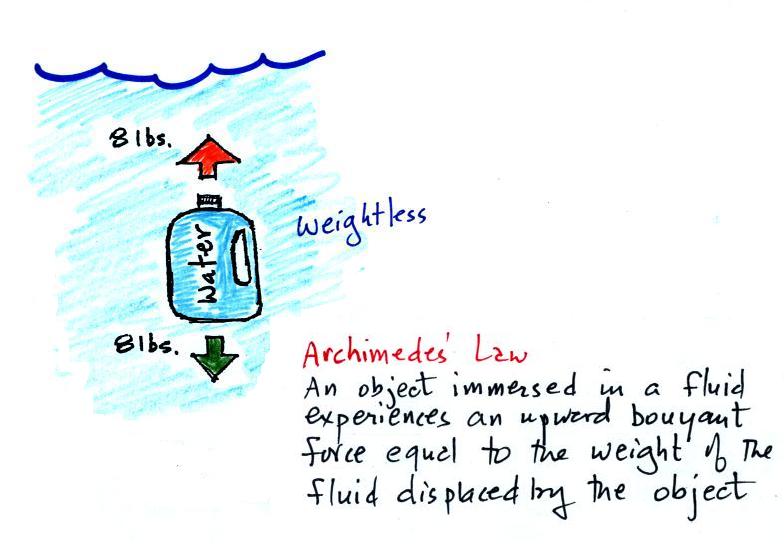
Archimedes first of all tells you that the surrounding fluid will exert an upward pointing bouyant force on the submerged water bottle.  That's why the submerged jug can become weightless. 

Archimedes law also tells you how to figure out how strong the bouyant force will be.  In this case the 1 gallon bottle will displace 1 gallon of pool water.  One gallon of pool water weighs 8 pounds.  The upward bouyant force will be 8 pounds, the same as the downward force.  The two forces are equal and opposite.

What Archimedes law doesn't really tell you is what causes the upward bouyant force.  If you're really on top of this material you will recognize that it is really just another name for the pressure difference force that we covered on Wednesday (higher pressure pushing up on the bottle and low pressure at the top pushing down, resulting in a net upward force).

Now we imagine pouring out all the water and filling the 1 gallon jug with air.  Air is about 1000 times less dense than water; compared to water,  the jug will weigh practically nothing.




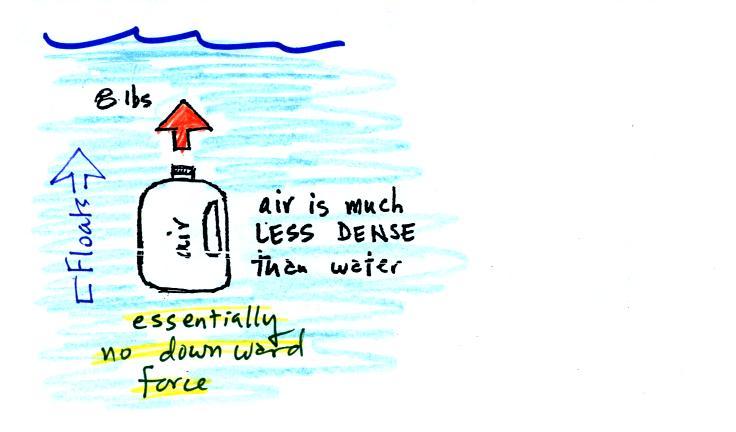
If you submerge the jug of air in a pool it will displace 1 gallon of water and experience an 8 pound upward bouyant force again.  Since there is no downward force the jug will float.

One gallon of sand (which is about 1.5 times denser than water) jug weighs 12 pounds (I checked this out because I like to try to give you accurate information).


The jug of sand will sink because the downward force is greater than the upward force.

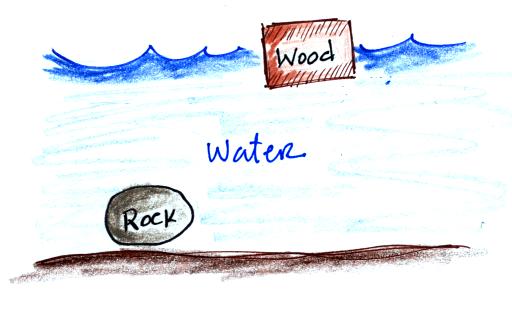
You can sum all of this up by saying anything that is less dense than water will float in water, anything that is more dense than water will sink in water.

Most types of wood will float.  Most rocks won't (pumice for example often floats).

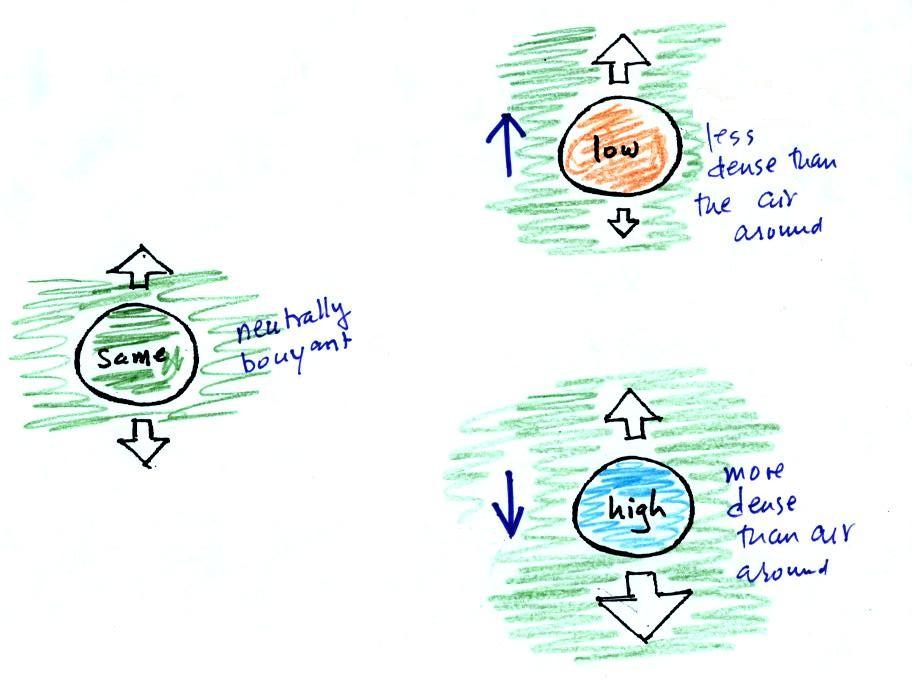
The same reasoning applies to air in the atmosphere.


Air that is less dense (warmer) than the air around it will rise.  Air that is more dense (colder) than the air around it will sink.


Here's a little more information about Archimedes that I didn't mention in class.

There's a colorful demonstration that shows how small differences in density can determine whether an object floats or sinks.

A can of regular Pepsi (actually it was Cherry Pepsi) was placed in a beaker of water.  The can sank.  A can of Diet Pepsi on the other hand floated.

Both cans are made of aluminum which has a density almost three times higher than water; aluminum by itself would sink.  The drink itself is largely water.  The regular soda also has a lot of high-fructose corn syrup, the diet soda doesn't.  The mixture of water and corn syrup has a density greater than plain water.  There is also a little air (or perhaps carbon dioxide gas) in each can.

The average density of the can of regular soda (water & corn syrup + aluminum + air) ends up being slightly greater than the density of water.  The average density of the can of diet soda (water + aluminum + air) is slightly less than the density of water.

I sometimes repeat the "demonstration" with a can of Pabst Blue Ribbon beer.  This also floats because the beer doesn't contain any corn syrup (I don't think). 

In some respects people in swimming pools are like cans of regular and diet soda.  Some people float (they're a little less dense than water), other people sink (slightly more dense than water). 

Many people can fill their lungs with air and make themselves float, or they can empty their lungs and make themselves sink.  People have an average density that is about the same as water.  That makes sense because we are largely made up of water (water makes up about 60% of human males and 55% of human females according to this source)

Finally here's the answer to the question found earlier in today's notes.

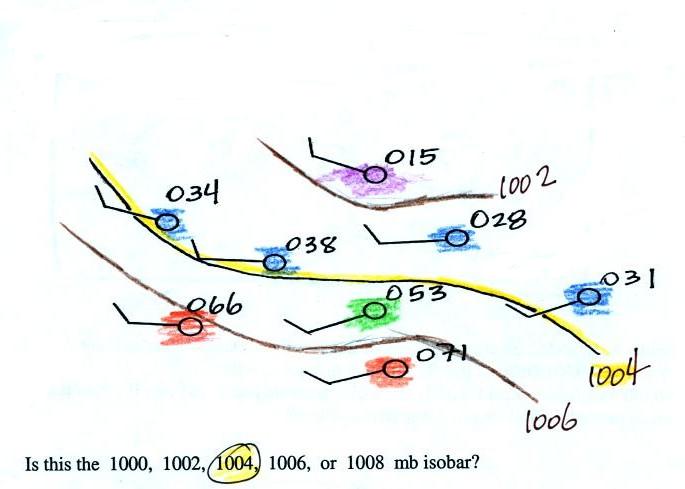
Pressures lower than 1002 mb are colored purple.  Pressures between 1002 and 1004 mb are blue.  Pressures between 1004 and 1006 mb are green and pressures greater than 1006 mb are red.  The isobar appearing in the question is highlighted yellow and is the 1004 mb isobar.  The 1002 mb and 1006 mb isobars have also been drawn in (because isobars are drawn at 4 mb intervals starting at 1000 mb, 1002 mb and 1006 mb isobars wouldn't normally be drawn on a map)