Thursday, Sept. 12, 2019
Jenny and the Mexicats "Frenetico
Ritmo" (0-2:50), "The Song for UV House Mouse" (3:05 - 8:15 =
5:10), appearing on NPR Tiny Desk Concert, "La Noche"
feat. Sandoval (4:24), "Llueve en el
Mar" feat. Juan Solo (0:45 - 5:39 = ~5:00). Jenny and
the Mexicats will be appearing tomorrow (Fri., Sept. 13) at the Rialto Theatre in
downtown Tucson.
We'll be using page
49, page 50, and page 51 from the ClassNotes
today.
We were able to just get started on this topic at
the end of class on Tuesday (Sept. 10)
Trying to understand why
warm air rises & cold air sinks

|

|

|
Hot air balloons floating over the Rio
Grande river during the 2013 Albuquerque Balloon Fiesta (source
of the photo)
|
Photograph of a microburst, a localized
intense thunderstorm downdraft, that hit Wittmann Arizona
in July 2015. Surface winds of 55 MPH were measured.
(source
of the photo)
|
Cold sinking air. The
air was cooled by coming into contact with a piece of dry
ice. (image source) |
A full understanding of these rising and sinking motions is a
3-step process (the following is found on page 49 in the photocopied
ClassNotes).
We will first learn about the
ideal gas law. It's is an equation that tells you which
properties of the air inside a balloon work to determine the
air's pressure.
Next we will look at Charles' Law, a special situation
involving the ideal gas law (air temperature volume, and
density change together in a way that keeps the pressure
inside a balloon constant). Then we'll learn about the 2
vertical forces that act on air. I'm pretty sure you
know what the downward force is and suspect that you don't
recall what the upward force is (hint we talked about it in
class on Tuesday ).
The ideal gas law - a microscopic scale explanation of
air pressure
We've spent a fair amount of time learning about
pressure. We first began with the idea that pressure is
determined by the weight of the air overhead. Air
pressure pushes down against the ground at sea level with 14.7
pounds of force per square inch. That's a perfectly
sound explanation.
We then went a bit further and tried to imagine the weight of
the atmosphere pushing down on a balloon sitting on the
ground. If you actually do push on a balloon you realize
that the air in the balloon pushes back (and sideways) with
the same force. Air pressure everywhere in the
atmosphere pushes upwards, downwards, and sideways.
These are large scale, atmosphere size, ways of thinking about
pressure. Next we are going to forget the atmosphere and
focus in on just the air in the balloon. This is more of a
microscopic view of pressure.
We'll
probably start at this point in class on Thursday
Imagine filling a balloon with air. If you could
look inside which picture below would be more realistic?
|
The view on the left is
incorrect.
The air molecules do not fill the balloon and
do not take up all the available space.
|
This is the correct
representation.
The air molecules are moving around at 100s of MPH
but actually take up little or no space in the
balloon.
|
The air molecules are continually colliding
with the walls of the balloon and pushing outward (this force
divided by area is the pressure). Wikipedia
has a
nice animation. An individual molecule doesn't
exert a very strong force, but there are so many molecules
that the combined effect is significant.
We want to identify the properties or characteristics of the
air inside the balloon that determine the pressure and then put
them together into an equation called the ideal gas law.
The ideal gas law equation
You're not going to have to be able to figure out or remember
the ideal gas law equation. I'll give it to you. Here
is is:
You should know what the symbols in the equation
represent. Probably the most obvious variable is N the
number of air molecules. It's
the motions of the air molecules that produce pressure. No
air molecules (N = 0) means no pressure. The more air
molecules there are the higher the pressure.
Number of gas molecules or atoms
Pressure (P) is
directly proportional to Number of air molecules (N). If N
increases P increases and vice versa.
Here's an example. You're adding air
to a tire. As you add more and more air to something like a
bicycle tire, the pressure increases. Pressure is directly
proportional to N; an increase in N causes an increase in P.
If N doubles, P also doubles (as long as the other variables in
the equation don't change).
Temperature
Here's what I think is the next most obvious variable.
You shouldn't throw a
can of spray paint into a fire because the temperature
will cause the pressure of the gas (propellant) inside
the can to increase and the can could explode.
So T (temperature) belongs in the ideal gas law equation
Increasing the
temperature of the gas in a balloon will cause the gas
molecules to move more quickly (kind of like "Mexican
jumping beans"). They'll collide with the
walls of the balloon more frequently and rebound with
greater force - that will increase the pressure.
We've gotten a little bit ahead of the story. The
variable V (volume) has appeared in the equation and it's in the
denominator. A metal can is rigid. It's
volume can't change (up until the moment the can explodes).
When we start talking about air in balloons or in the atmosphere
volume can change. A change in temperature or a change in
number of air molecules might be accompanied by a change in
volume. Balloons and cans of spray paint are sealed, so N
also stays constant.
At this point we did a quick demonstration to show the effect
of temperature on the pressure of the gas in a rigid sealed
container (N and V in the ideal gas law equation stay constant,
just as in a can of spray paint).
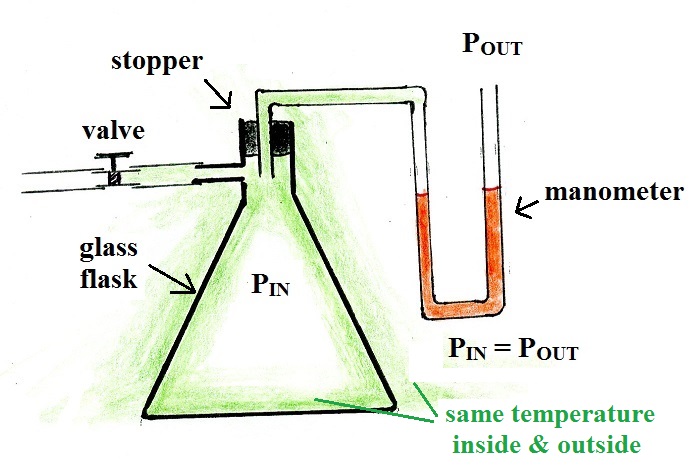
The container was a glass flask, sealed with a rubber
stopper. A piece of tubing with a valve was connected to the
flask. The valve was opened at the start of the
demonstration to be sure the pressures inside and outside the
flask were equal. The valve was then closed. The
manometer is a U-shaped tube filled with a liquid (transmission
oil) that can detect differences in pressure. Pressure from
the air inside the flask could enter one end of the manometer
tube. The other end was exposed to the pressure of the air
outside the flask.
Green in the figure indicates that the temperatures of the air
inside and outside the flask were equal. The manometer is
showing that the pressure of the air inside and outside the flask
were equal.
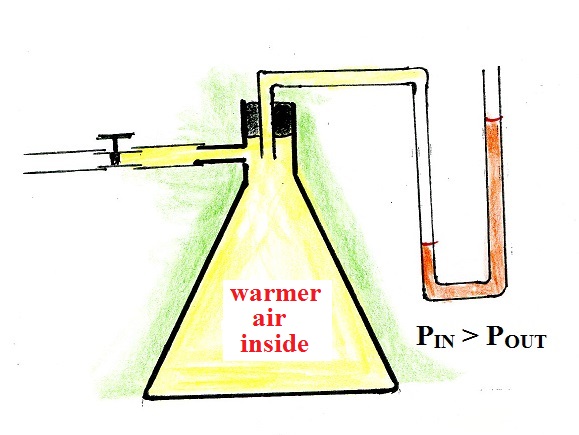
I wrapped my hands around the flask to warm the air inside very
slightly. The increase in air temperature caused a slight
increase in the pressure of the air inside the flask. The
air outside didn't change. Note the change in the levels of
the liquid in the manometer indicating the increase of the air
pressure inside the flask.
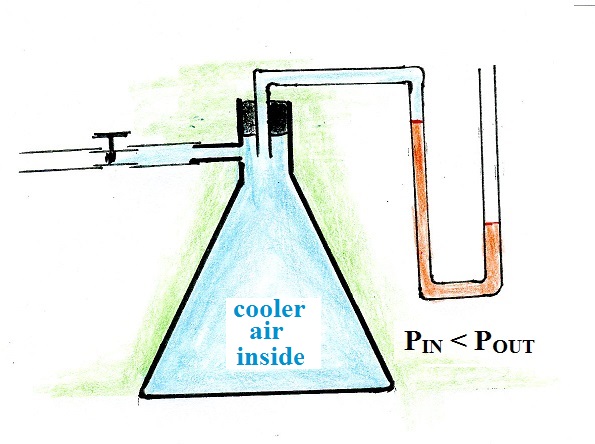
The valve was opened momentarily so that the pressures inside
and out would again be equal. The valve was then closed and
some isopropyl alcohol (rubbing alcohol) was dribbled on the
outside of the flask. As the alcohol evaporated it cooled
the flask and the air inside the flask. This caused the air
pressure inside the flask to drop. This change in air
pressure was again indicated by the liquid levels in the
manometer.
Volume
The effect of volume on pressure might be a little harder to
understand. Just barely fill a balloon with air, wrap your
hands around it, and squeeze it. It's hard to compress the
balloon, you can't really compress it very much at all.
Think of the bottom layer
of the atmosphere being squished by the weight of the air
above. As the bottom layer is compressed and its volume
shrinks it pushes back with enough force to eventually support
the air above.
A decrease in volume
causes an increase in pressure, that's an inverse
proportionality.
It might take three or four
breaths of air to fill a balloon. Think about
that. You add some air (N increases) and the balloon
starts to inflate (V increases). Then you add another
breath of air. N increases some more and the balloon
gets a little bigger, V has increased again. As you
fill a balloon N and V are both increasing. What is
happening in this case is that the pressure of the air in
the balloon is staying constant. The
pressure inside the balloon pushing outward and trying to
expand the balloon is staying
equal to (in balance with) the pressure of the air outside
pushing inward and trying to compress the balloon.
Here's the same picture again except N and V
are decreasing together in a way that keeps pressure
constant. This is exactly what occurs during Experiment
#1.
Experiment #1
- P stays constant, N & V both decrease
Here's a little more detailed explanation of Expt. #1
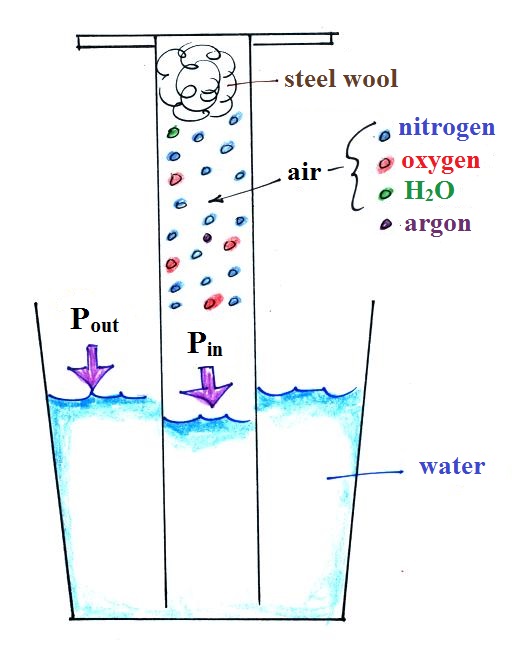
|
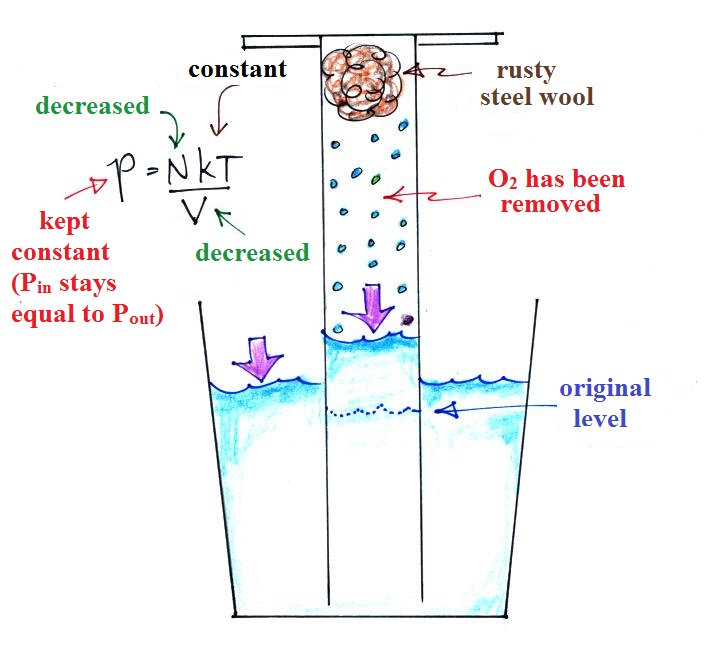
|
The object of
Experiment #1 is to measure the
percentage concentration of oxygen in
the air.
An air sample is
trapped together with some steel wool inside a graduated
cylinder. The cylinder is turned upside down and
the open end is stuck into a glass of water sealing off
the air sample from the rest of the atmosphere.
This is shown at left above. The pressure of air
outside the cylinder tries to push water into the
cylinder, the pressure of the air inside keeps the water
out.
Oxygen in the cylinder reacts with
steel wool to form rust. Oxygen is removed from
the air sample which causes N (the total number of air
molecules) to decrease. Removal of oxygen would
ordinarily cause a drop in Pin
and
upset the balance between Pin
and Pout
. But, as oxygen
is removed, water rises up into the cylinder decreasing
the air sample volume. The decrease in V is what
keeps Pin
equal to Pout
.
N and V both decrease together in the same relative
amounts and the air sample pressure remains constant.
If you were to remove 20% of the air molecules, V would
decrease to 20% of its original value and pressure would stay
constant. It is the change in V that you can see, measure,
and use to determine the oxygen percentage concentration in
air. Those of you doing the experiment should try to
explain this in your experiment report.
You might think that the mass of the gas molecules inside a
balloon might affect the pressure (big atoms or molecules might
hit the walls of the balloon harder and cause higher pressure
and vice versa).
The mass of the air molecules doesn't matter. The big ones
move relatively slowly, the smaller ones more quickly.
They both hit the walls of the balloon with the same
force. A variable for mass doesn't appear in
the ideal gas law equation.
The ideal gas law equations
The figure below shows two forms of the ideal gas law. The
top equation is the one we've been looking at and the bottom is
a second slightly different version. You can
ignore the constants k and R if you are just trying to
understand how a change in one of the variables would affect the
pressure. You only need the constants when you are doing a
calculation involving numbers and units (which we won't be
doing).
The ratio N/V is similar to density
(mass/volume). That's where the ρ (density)
term in the second equation comes from.