Monday Mar. 19, 2018
Dessa "Fighting Fish"
1st of a 3-song set on NPR Music Tiny Desk Concert (3:05), "Matches to
Paper Dolls" Audiotree Live (3:08),
"551"
89.3 The Current (4:14), "Skeleton Key"
(3:38) Audiotree Live, "Mineshaft II"
Minnesota Original (4:42)
A take
home Optional Assignment was handed out in class
today. I'll have additional copies in class on
Wednesday. It is due at the start of class next Monday, Mar.
26.
Humidity variables review
Before we get to the first of two or three humidity example
problems that it would probably be wise to quickly review
of the 4 humidity variables introduced in Friday's
class. If you were in class you can probably just
quickly skim through or even skip the following (the questions
are from the Friday Optional In-class Assignment).
1.
Mixing ratio has units of grams per kilogram (g/kg)
Here's another question (and answer) from last week's in-class
optional assignment
The mixing ratio only changes value when you add or remove water
vapor.
If you cool the air enough you can cause water vapor to start to
condense. The air is losing water vapor, the amount of water
vapor in the air is decreasing. Mixing ratio will decrease
in that case.
2.
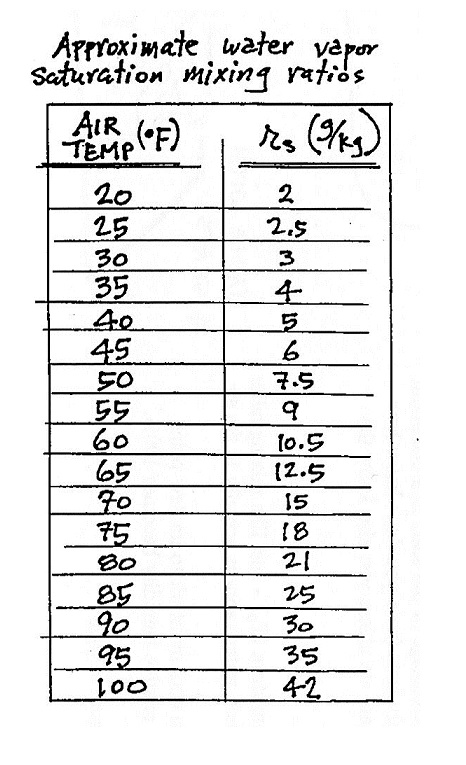
Saturation mixing ratio also has units of grams/kilogram.
You can look the value of saturation mixing ratio up in a chart
(like the one of p. 84 in the ClassNotes)
Here are a few more questions from last week's optional
assignment
We'll work some humidity example problems. This is the
way to become more familiar with the humidity variables: how
they behave and what causes them to change value. We'll
make use of the table of saturation mixing ratios on p. 84 and
the charts on pps 85 & 86 in the ClassNotes.
3.
The relative humidity really doesn't tell you how
much water vapor is actually in the air.
4.
The dew point temperature has a couple of
jobs. Here's the one we'll be using today
Cooling air doesn't change the mixing
ratio. As you cool air the saturation mixing ratio
decreases. Eventually the values of the mixing ratio and
saturation mixing ratio become equal and the RH becomes 100%.
This is the dew point's other job. One of the example
problems will try to show that if you know the dew point
temperature you can easily figure out the mixing ratio and
vice versa.
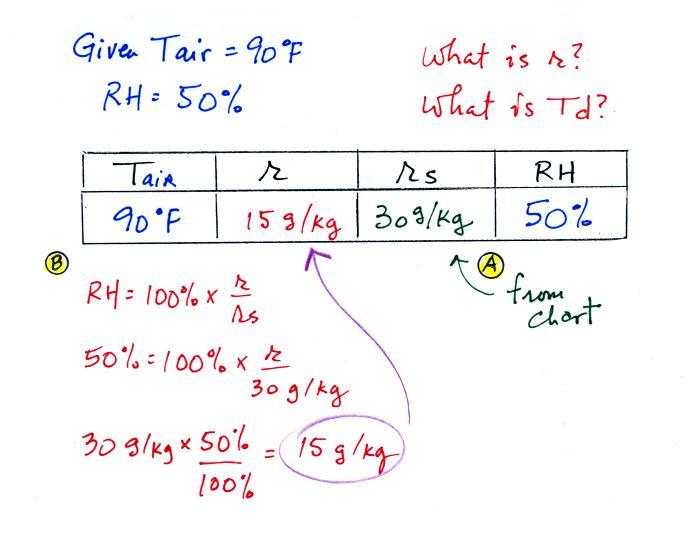
Humidity example problem #2
Tair = 90 F
|
r = ?
|
| RH = 50% |
Td = ?
|
The problem is worked out in detail below
First you fill in the air temperature and the RH data that
you are given.
(A) since you know the air's temperature you can look up the
saturation mixing ratio (30 g/kg).
(B) Then you might be able to figure out the mixing ratio
in your head. Air that could hold up to 30 g/kg of water
vapor is filled to 50% of its capacity. Half of 30 is 15,
that is the mixing ratio. Or you can substitute into the
relative humidity formula and solve for the mixing ratio.
The details of that calculation are shown above at B.
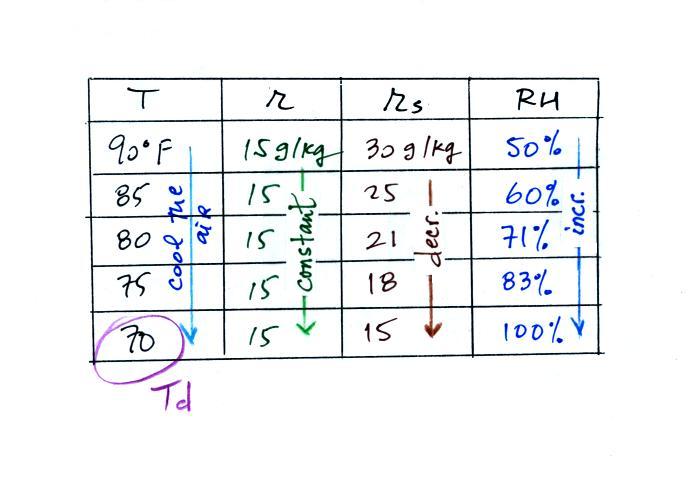
Finally you imagine cooling the air (I
added more intermediate temperatures in the table above than
we use in class). Notice how the saturation
mixing ratio decreases, the mixing ratio stays constant, and the
relative humidity increases as the air is cooled. In
this example the RH reached 100% when the air had cooled to 70
F. That is the dew point temperature.
What does
the difference Tair - Td tell you about the relative
humidity?
We
can use results from humidity problems #1 and #2
to learn and understand a useful rule.
In the first example the difference between the air and dew
point temperatures was large (45 F) and the RH was low (20%).
In the 2nd problem the difference between the air and dew point
temperatures was smaller (20 F) and the RH was higher
(50%).
The easiest way to remember this rule might be to remember the
case where there is no difference between the air and dew point
temperatures.
The RH then would be 100%.
We'll probably skip the next
problem in class but I'll include it here in the notes.
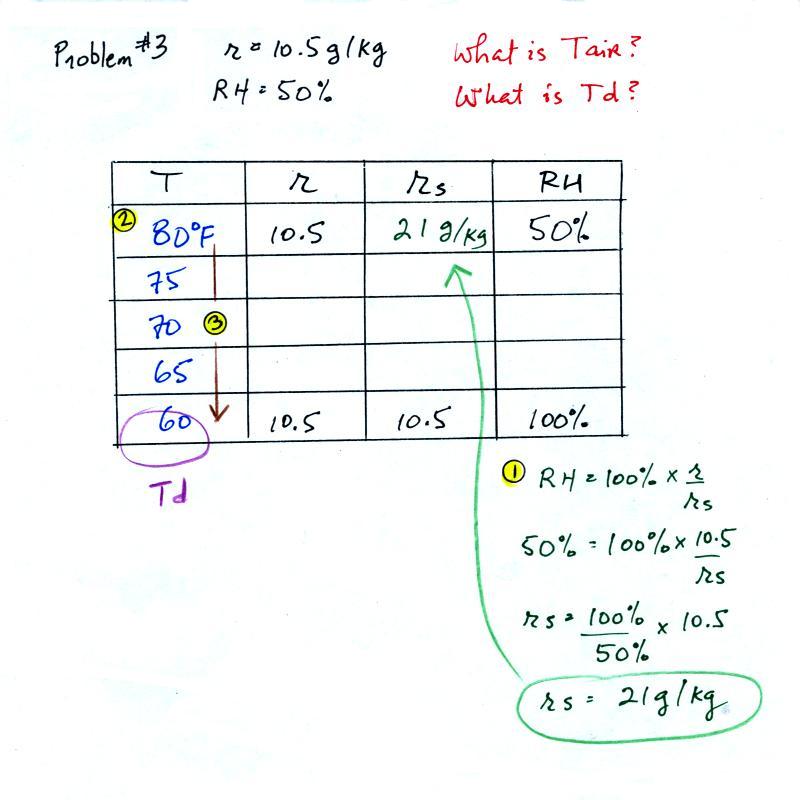
Humidity example problem #3
Tair = ?
|
r = 10.5 g/kg
|
| RH = 50% |
Td = ?
|
You're given the the mixing ratio = 10.5 g/kg and a relative
humidity of 50%. You need to
figure out the air temperature and the dew point temperature.
Give it a try. A step by step solution is given below:
(1) The air contains 10.5 g/kg of water vapor. This is 50%
(half) of what the air could potentially hold. So the
air's capacity, the saturation mixing ratio must be 21 g/kg (you
can either do this in your head or use the RH equation following
the steps shown above).
(2) Once you know the saturation mixing ratio you can look up
the air temperature in a table (80 F air has a saturation mixing
ratio of 21 g/kg)
(3) Then you imagine cooling the air until the RH becomes
100%. This occurs at 60 F. The dew point is 60 F
One of the "jobs" of the dew point, to give you
an idea of the actual amount of water vapor in the air, is
the same as the mixing ratio. The next problem will
demonstrate that if you know the dew point temperature you
can quickly figure out the mixing ratio and vice versa.
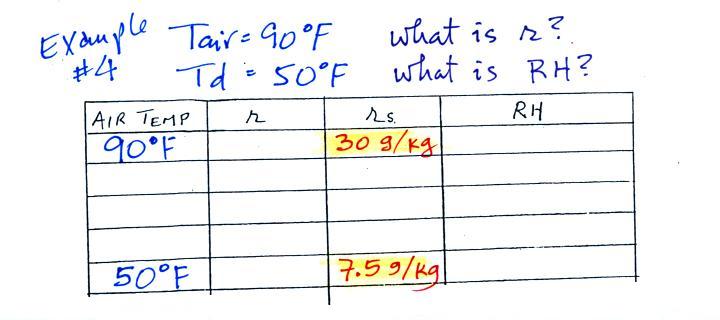
Humidity example problem #4
Tair = 90 F
|
r = ?
|
RH = ?
|
Td = 50 F
|
One of the dew
point's jobs is the same as the mixing ratio - it gives
you an idea of the actual amount of water vapor in the
air. This problem will show that if you know the
dew point, you can quickly figure out the mixing ratio
and vice versa. Knowing the dew point is
equivalent to knowing the mixing ratio.
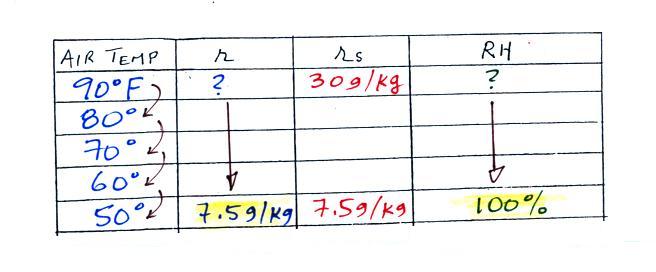
We enter the two temperatures given on a chart and look up the
saturation mixing ratio for each.
We ignore the fact that we don't know the mixing ratio. We
do know that if we cool the 90 F air to 50 F the RH will become
100%. So on the 50 F row, we can set the mixing ratio
equal to the value of the saturation mixing ratio at 50 F, 7.5
g/kg. The two have to be equal in order for the RH to be
100%.
Remember back to the three earlier examples. When
we cooled air to the the dew point, the mixing ratio didn't
change. So the mixing ratio must have been 7.5 all
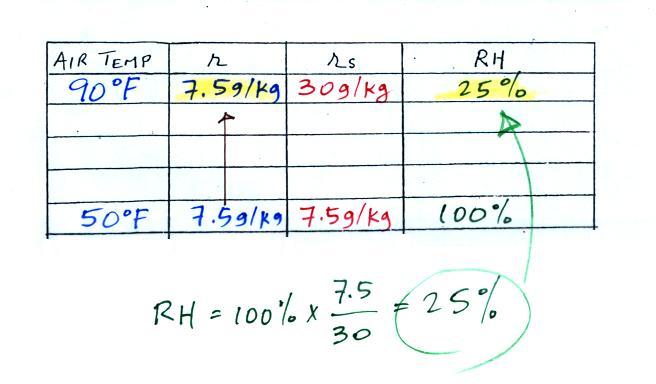
along. Once we know the mixing ratio in the 90 F air
it is a simple matter to calculate the relative humidity, 25%.
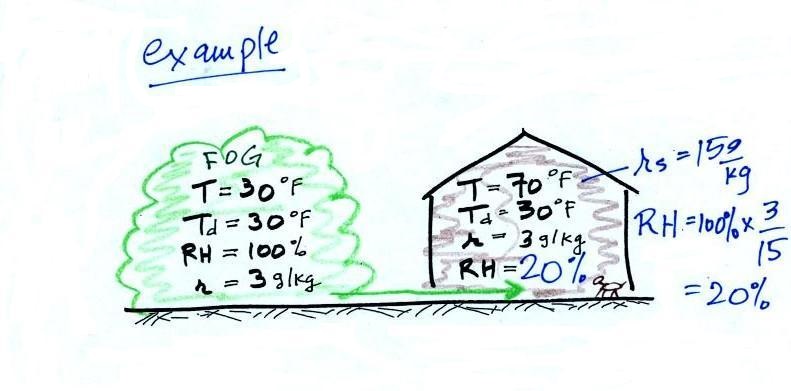
Drying moist air
The figure below is on p. 87 in the photocopied ClassNotes.
It
explains how you can dry moist air.
At Point 1 we start with some 90 F air with a relative
humidity of 25%, fairly dry air. These are the same
numbers that we had in Example Problem #4. We imagine
cooling this air to the dew point temperature, 50 F. While
doing that the mixing ratio, r, would stay constant.
Relative humidity would increase and eventually reach
100%. A cloud would form (Pt. 2 in the figure
above).
Then we continue to cool the air below the dew point, to 30
F. Air that is cooled below the dew point finds itself
with more water vapor than it can contain. The excess
moisture must condense (we will assume it falls out of the air
as rain or snow). Mixing ratio will decrease, the relative
humidity will remain 100%. When air reaches 30 F it
contains 3 g/kg, less than half the moisture that it originally
did (7.5 g/kg).
The air is being warmed back up to 90 F along Path 4. As
it warms the mixing ratio remains constant. Cooling moist
air raises the RH. Warming moist air, as is being down
here, lowers the RH. Once back at the starting
temperature, Point 5, the air now has a RH of only 10%.
Drying moist air is basically wringing moisture from a wet
sponge.
You start to squeeze the sponge and it gets
smaller. That's like cooling the air and reducing the
saturation mixing ratio, the air's capacity for water
vapor. At first squeezing the sponge doesn't cause
anything to happen (that's like cooling the air, the mixing
ratio stays constant as long as the air doesn't lose any water
vapor). Eventually water will start to drop from the
sponge (with air this is what happens when you reach the dew
point and continue to cool the air below the dew point).
Then you let go of the sponge and let it expand back to its
original shape and size (the air warms back to its original
temperature). The sponge (and the air) will be drier than
when you started.
Dry air indoors in the winter
The air indoors in the winter is often quite dry
(low values of the mixing ratio and relative humidity).
In the winter, cold air is brought inside your house
or apartment and warmed. Imagine foggy 30 F air (with a RH
of 100% this is a best case scenario, the cold air outdoors
usually has a relative humidity less than 100% and is drier).
Bringing the air inside and warming it will cause the RH to drop
from 100% to 20%.. This can cause chapped skin, can
irritate nasal passages, and causes cat's fur to become charged
with static electricity.

The air in an airplane comes from
outside the plane. The air outside the plane can
be very cold (-60 F perhaps) and contains very little
water vapor (even if the -60 F air is saturated it would
contain essentially no water vapor). When brought
inside and warmed to a comfortable temperature, the RH
of the air in the plane would be essentially 0%.
The RH doesn't get this low because the airplane adds
moisture to the air to make to make the cabin
environment tolerable. Still the RH of the air
inside the plane is pretty low and passengers often
complain of dehydration
on long airplane flights. This
may increase the risk of catching a cold (ref)
The Spring Equinox
We'll probably journey
over to the 1S1P
topic on the Equinoxes and Manhattanhenge at this
point - there are some phenomena you should try
to observe the next few days.
First of all
the days and nights are each 12 hours long. I
believe that is what the name equinox is referring
to. In Tucson the sun rises around 6:30 am and
sets at 6:30 pm. The sun has been rising earlier
and the days have been getting longer all
semester. I'm able to ride my bike to school on
Tuesday and Thursday morning now for my 8 am class in
daylight, that wasn't the case early in the semester.
Second, and this is the one to look for, the sun rises
exactly in the east and sets exactly in the west.
If you're out driving on an east-west oriented street
around sunrise or sunset you'll see this. There's
a good chance the sun will be directly in your eyes.
On the
equinoxes the sun will be directly overhead at noon at
the equator. There is often a narrow band of
clouds visible on a satellite photo of the globe
wherever the sun is passing overhead at noon (at the
equator on the equinoxes, at the Tropic of Cancer (23.5
N latitude) on the June 21 summer solstice and at the
Tropic of Capricorn (23.5 S latitude) on the Dec. 21
winter solstice. The clouds are forming above
something called the Intertropical Convergence Zone,
it's a belt of low pressure that circles the globe and
will probably be part of a future 1S1P topic.
Gallery
of satellite images showing clouds that form above the
Intertropical Convergence Zone (ITCZ)
Here is another good source of
satellite images: http://www.ssec.wisc.edu/data/composites