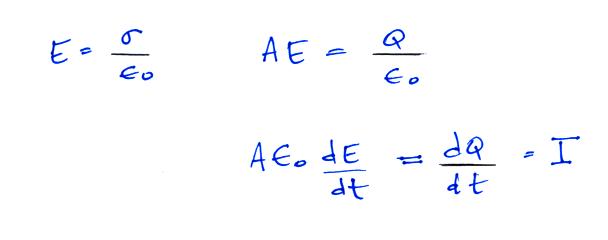We obtain Poisson's Equation. Laplace's equation
applies in situtations where the volume space charge
density is zero. We'll be using Laplace's equation
in our next lecture. Here is a handout with vector
differential operators (Laplacian, curl, gradient
and divergence) in cartesian, cylindrical, and spherical
coordinate systems.
Now some applications of
what we have been learning. In this and the next
class we'll looking at a couple of instruments used to
measure thunderstorm and lightning electric fields.
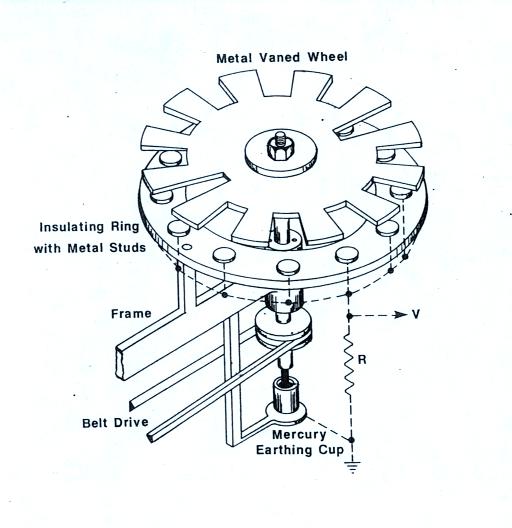
The first is an
electric field mill used to measure static and slowly
time varying electric fields. Referring to the
figure below at left (from Uman's 1987 The Lightning
Discharge book). The sensors (referred to as
studs in the figure) are covered by a rotating
grounded plate. The rotating plate is notched or
slotted so that the sensors are periodically exposed
to and covered (shielded) from the ambient electric
field. A photograph of the field mill shown in
class is shown below at right (signal and power cables
are connected at the bottom of the mill).
The two photographs below are closeups of the top of
the field mill
The stator plates are exposed to the E field at left
and covered in the photograph at right. The four
stators (sensor plates) exposed in the figure at left are
connected together electrically. Another four
stators, also connected together are exposed in the figure
at right. Thus this field mill has two sets of
sensors. One is exposed while the other set is
covered. This just makes it possible to make
measurements of the E field two times more often.
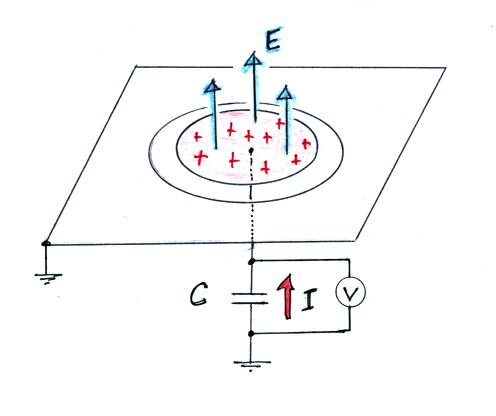
The next figure shows currents flowing into and out of
the sensor plate in response to an incident E field.
The sensor plate is covered at Point 1. At Point
2 the sensor is uncovered and we assume the ambient field
points upward (toward negative charge in the lower part of
a thunderstorm perhaps). Positive charge flows up to
the sensor plate. The current flows from the sensor
in Point 3 because the sensor has been covered and
shielded from the E field. Points 4 and 5 are
similar except the polarity of the E field has been
changed.
Note the current signals at Points 2 & 5 are the
same even though the field polarities are reversed.
You must keep track of when the sensor is covered and
uncovered in order to determine the polarity of the
incident E field.
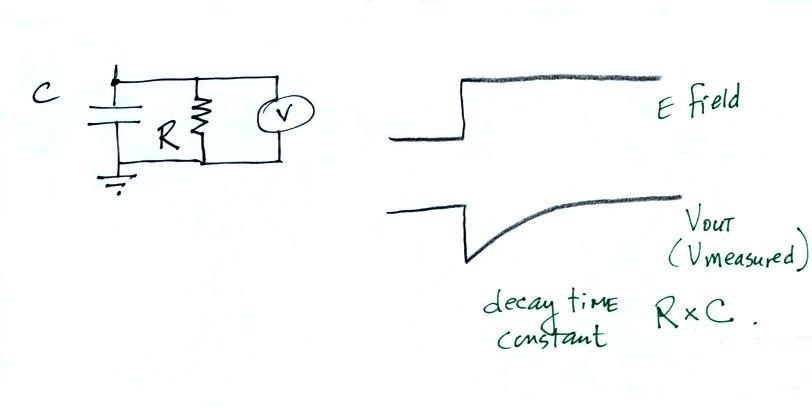
It is a relatively simple matter to relate the
amplitude of the signal current to the intensity of the
incident E field.