Thursday Feb. 16, 2017

Life cycle of small ions
On to the main part of today's class.  The lifetime of a small ion is sketched below.  This will serve to introduce what we'll be covering today.


The first step is ionization of an air molecule.  We discussed the sources of this ionizing radiation in class on Tuesday.  A cosmic ray is shown in the figure above.  We'll be interested in how long it takes the free electron that is created in this first step to attach to an oxygen molecule (it turns out to be very quick, just a few or a few tens of nanoseconds).  Water vapor molecules then cluster around the charged air molecule to form small ions.  This step is also pretty fast, occurring in milliseconds. 

Once created the small ions can recombine.  Whatever results is uncharged.  We'll write down an ion balance equation with a small ion creation term and a recombination term, a loss term. 

Or the small ions can attach to much larger particles in the air.  This lowers their mobility.  There charged particles are known as "large ions."  We'll discuss this in class today also.

Small ion balance equation
What happens to the small ions once they are created?  How long do they survive?  For that we need an ion balance equation.


The concentration of small ions (the positively charged ions are considered in the first equation) will depend on the ion production rate, q, and the rate at which ions recombine and neutralize each other.  Because the free electrons attach to oxygen molecules so rapidly and the clustering of water vapor molecules around charged molecules is also quick they don't slow down the formation of small ions.  The key step in the formation of small ions is the rate of ionization.  Be sure to note that q is ionization rate in this equation, not electrical charge.

A simpler version of the equation (the bottom equation above) can be written if we assume that the concentrations of positive and negative small ions are equal.

The next figure gives the general and steady state solutions to the ion balance equation.



We get the steady state concentration as t goes to infinity.  At steady state, dn/dt is zero so here's a shorter, easier way of detemining the steady state solution.
How long does it take to get to steady state?


The 2√(αq) t term doesn't really need to be very big before you start to approach steady state.

.


You get to steady state pretty quickly, 2√(αq) t = 5 is probably sufficient.  The 134 seconds value above is about two minutes, so we approach steady state in ~10 minutes when q = 10 ip/cm3 sec (it would take about 30 minutes if q = 1 ip/cm3 sec.  We're really not going to be looking at fair weather phenomena that happen more quickly than that.
Next we can calculate the steady state concentration and then the lifetime of a typical small ion (concentration divided by production rate or by recombination rate since they are equal at steady state)


Remember that n is the concentration of either the positive or negative small ions (which we have assumed have equal concentrations).

We can also estimate the conductivity (remembering that both positive and negative small ions contribute to the conductivity and taking into account that the positive and negative small ions have slightly different electrical mobilities).  We assume that the small ions carry a single electronic charge.


This seems a little high (maybe 5 times higher than values we've been using in class and on homework assignments).  But this is a case where there are just small ions and no particles.  We'll look at the effects of particles in class on Friday.   Particles are an additional small ion loss process and we would expect that to lower the equilibrium concentration of small ions.  That will also reduce the conductivity.

Small ion attachment to particles
 A small ion can attach to an uncharged particle, creating a charged particle or a so-called "large ion". 




Or a small ion of one polarity can attach to a charged particle of the opposite polarity creating an uncharged particle (provided the small ion and the particle have equal quantities of charge).  These two new terms are included in the small ion balance equation below.  The β+o and β+- terms are referred to as "attachment coefficients."



We often assume that the concentrations of positive and negative small ions and the concentrations of positively and negatively charged particles are equal.  Let's also make the following assumptions concerning the attachment coefficients.

The balance equation then becomes

The bottom equation is just an additional simplification of the top equation.  A total particle concentration term, Z, is used rather than keeping track of the concentrations of charged and uncharged particles.  This is the form of the equation we'll use in most situations.

The figure below (from The Earth's Electrical Environment reference) illustrates how ion-particle attachment begins to significantly reduce small ion concentrations beginning at particles concentrations of about 1000 cm-3.  Clean air typically has 100s of particles per cc while dirtier air would contain 1000s of particles per cc.


You might remember the research vessel Carnegie mentioned near the start of the semester.  In addition to measurements of electric field (the Carnegie curve) measurements of atmospheric conductivity were also made.  The instrumentation has changed little since then.  Atmospheric conductivity depends on the concentration of small ions which we now see is  affected by particle concentrations.  There is no question that increased combustion of fossil fuels have increased atmospheric carbon dioxide concentrations; there is concern that this might cause global warming.  You might also expect combustion to add particles to the atmosphere.  Thus a comparison of atmospheric conductivity made in the early 1900s with measurements made today might provide some indication of whether atmospheric particulate concentrations have changed.  Atmospheric conductivity measurements might be another example of proxy data that might be used to track climate change.

Fractions of particles that are charged and uncharged
We sometimes spend some time looking at the numbers of particles that are charged and uncharged.  Here are some of the details if you are interested.  Otherwise a graphical summary of the results is sufficient.  No in the figure below is the uncharged particle concentration, Z is the total particle concentration.


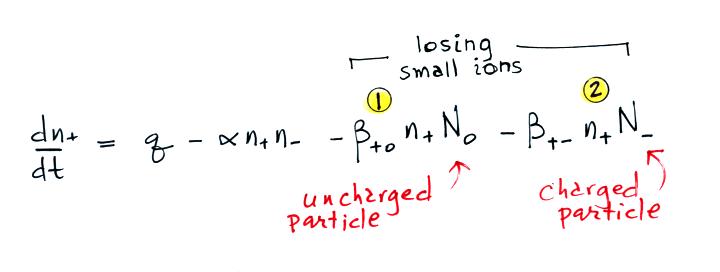
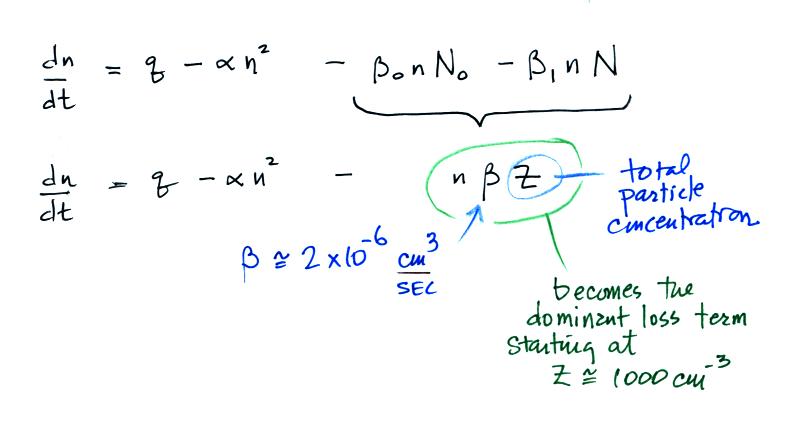
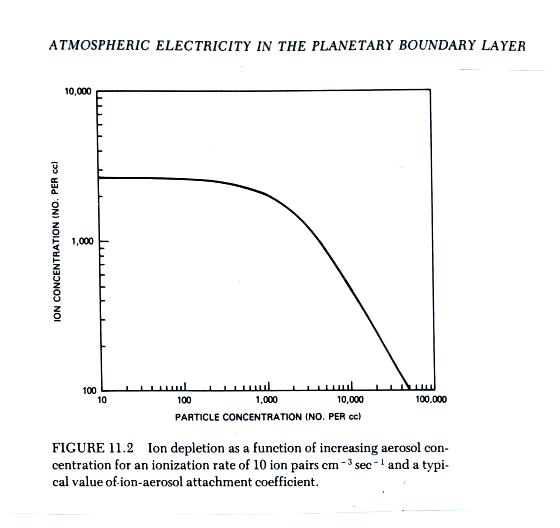
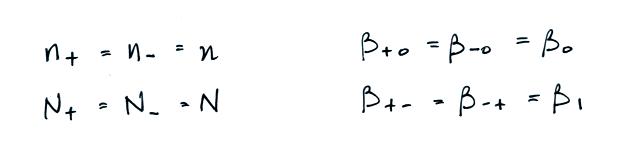Most smaller particles are uncharged.  The chart shows that roughly 90% of particles with a diameter of 10   cm are uncharged.  Small particles that are charged generally only carry one electron charge.  For larger particles the numbers of particles that are uncharged, positively charged, and negatively charged are roughly equal.  I.e. 1/3 of large particles are positively charged, 1/3 are negatively charged, and 1/3 are uncharged.
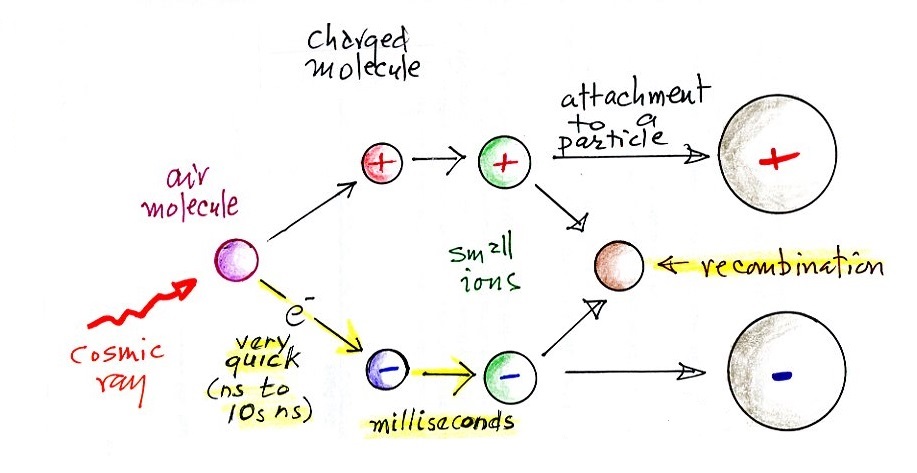
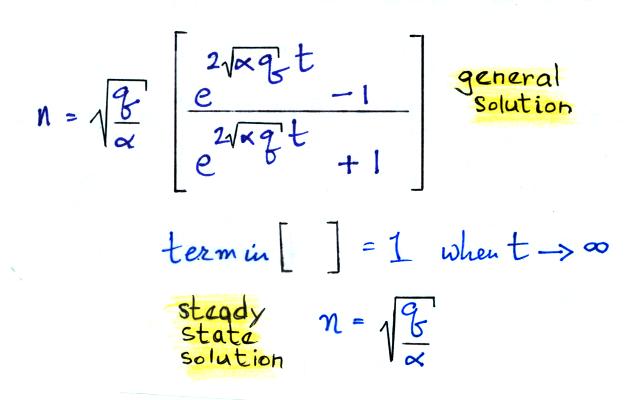
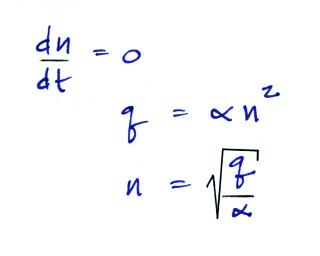