Tuesday March 28, 2017

Homework Assignment #6 pt. 1 was handed out in class today.  That assignment, together with pt. 2 of the assignment (which I plan to hand out in class on Thursday), will be due on Thursday Apr. 3.  You'll find some discussion of HW#6 pt. 1 further on in today's notes.

A paper by Rakov and Uman (1998) and Chapter 6 in Rakov's book "Fundamentals of Lightning"  provide very complete and detailed coverage of much of what we will be covering in this class.

Models of the lightning return stroke channel current, I(z,t)

In a couple of previous classes we looked at measurements of lightning return stroke current made in strikes to instrumented towers and in rocket-triggered lightning discharges.    It would be nice, and probably much easier, to be able to measure electric (E) and/or magnetic (B) fields and then go back and figure out what the current that produced those fields must have been.  But the electric (E) and magnetic (B) fields radiated by a lightning discharge depend in a complex way on return stroke current, the current derivative, and, for E fields, on the time integral of the current.  We have a pretty good idea of what lightning return stroke currents at ground level look like, but how does the current change as the return stroke propagates upward from the ground to the cloud.  We are going to need to simplify matters by making some simplifying assumptions or putting some constraints on the return stroke current   We will need a lightning return stroke "current model."

Before getting into the details there are at least a couple of other possible ways of determining lightning currents

1.  Sophisticated plasma-fluid-dynamics models that try to realistically determine the actual physical conditions in a lightning channel (temperature, electron density, pressure, and other electrical and fluid properties).   This is not easy and is well beyond the level of this class.   Have a look at Plooster (1971a & 1971a) if you'd like to see and example of this type of approach.

2.  Because the return stroke current usually starts at (or near) the ground and travels upward along a conducting channel, many researchers treat the return stroke as a voltage or current pulse traveling along a transmission line with distributed resistance, inductance, and capacitance. (see ,for example, Little (1978), and Price and Pierce (1977) ).

We will adopt more of an engineering or empirical approach
3.  We will assume a functional form for I(z,t), calculate the E and B fields that such a current would produce, and then compare the calculations with field measurements (sometimes made at two distances from the return stroke).  We will then adjust I(z,t) or other model parameters such as propagation speed to get the best agreement between calculated and measured fields.  There do seem to be situations where this type of approach will lead to reasonable estimates of parameters such as peak current and peak current derivative.

Before we get into any of the details let's review schematically what happens during a return stroke.  When a stepped leader (or dart leader) channel approaches the ground an upward connecting discharge is initiated and grows up to intercept the leader.  Because the leader channel is conducting we'll assume that bottom end of the leader is at about cloud potential.  The tip of the upward connecting discharge is at ground potential.  There's a very big potential difference between the two and intense fields in the gap ionizes (breaks down) the air and is the cause of the big currents that occur at the beginning of a lightning strike.  As charge flows out of the bottom end of the leader channel and flows to ground, the potential difference gap moves upward and big currents develop higher up in the channel.  The process continues and repeats itself and a "wave" of potential difference travels up the lightning channel.


Now let's look at three different return stroke current models.  In each case we will assume that the lightning channel is straight and vertical and that the potential difference gap (breakdown wave) moves up the channel at a constant speed (about one-third the speed of light).

Bruce Golde (BG) Model
This was one of the first models proposed (See Bruce and Golde (1941)).



In the Bruce Golde model the return stroke current is assumed to be uniform along the length of the channel.  Current begins at the ground and travels upward.

The current amplitude can change with time but it does so along the entire length of the channel simultaneously.  This is illustrated further in the figures below which shows the height of the return stroke channel and the current distribution along the channel at evenly spaced time intervals t1 through t5 (full picture at left, a portion of the figure with additional explanation at right).  The width of each vertical bar indicates the current amplitude.  As the current amplitude is changing at the ground with time, current amplitude also changes simultaneously along the entire length of the channel (this is of course unrealistic because it would mean a change at one point on the channel would need to be communicated to the rest of the channel at infinite speed). 













 
The current waveform measured at the ground and at Pt. B above the ground are shown at the bottom of the figure.  Current at Pt. B doesn't begin until t = t3 , the time that the breakdown zone (potential difference gap)  reaches altitude z3.  From t3 onward, the current waveforms measured at the ground and at Pt. B are identical. 



Here is an expression for the radiation field component of the electric field (Erad) at a distance D from the lightning stroke.  There are a few tricks involved in this derivation of this equation (that we won't worry about) because the current is discontinuous at the tip of the upward propagating return stroke current.  The expression for E can be inverted to give the channel base current as a function of the field (the last equation in the figure above).  Again we won't worry about the details.

Transmission Line (TL) Model
It is easy to visualize what happens when you connect a signal to a wire


The signal travels from one end of the wire without changing shape.

This is the basic idea in the transmission line model of return stroke current (you'll see it abbreviated TL and XL in these notes).  A current waveform measured at the ground is assumed to propagate up the channel at constant speed without changing shape.  Here's how that is expressed in equation form.


Basically you see the same current waveform at height z as you would see at the ground but it's delayed in time.  It takes time t = z/v for the current to travel from the ground to height z.     A picture might make this clearer.




The current waveform measured at the ground propagates up the channel without changing shape or speed.  The same current waveform would be seen at all points on the channel just delayed with respect to the ground.

There are a couple of modifications that have been made to the transmission line model that we'll mention.  In the MTLL model (Modified Transmission Line model with Linear decay) the amplitude of the current waveform decreases linearly with increasing altitude.  The I(t - z/v) expression above would be multiplied by (1 - z/H) where H is the top of the lightning channel.  The other is the MTLE (Modified Transmission Line model with Exponential decay).  The I(t - z/v) term decays exponentially with height, I(t - z/v) is multiplied by e-z/λ .

It is not too difficult to determine what the radiation component of the electric field (Erad) at distance D, so we'll go into some of the details.  The top equation below is the expression for the radiation field produced by a channel segment dz located a height z above the ground.  We're going to assume that we're far enough away from the lightning channel that D >> H (H is the total height of the lightning channel).   θ is about 90 degrees so sin(θ) is close to 1, and R is constant (R = D).


Because of the functional form of I(z,t), we can replace the partial derivative with respect to time with a partial with respect to z.



This makes it easy to integrate dErad over z.



The first term in brackets is zero at times less than H/v (i.e. before the return stroke tip reaches the top of the channel).

Try to understand and remember these transmission-line model equations


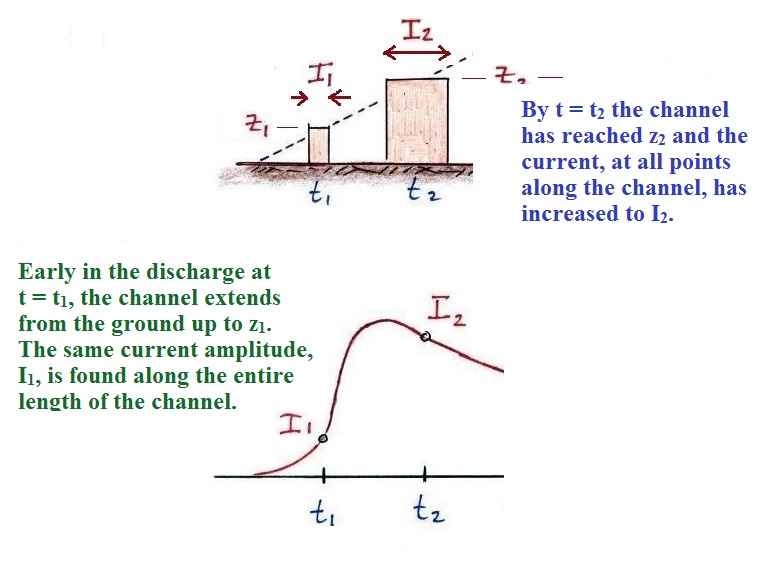
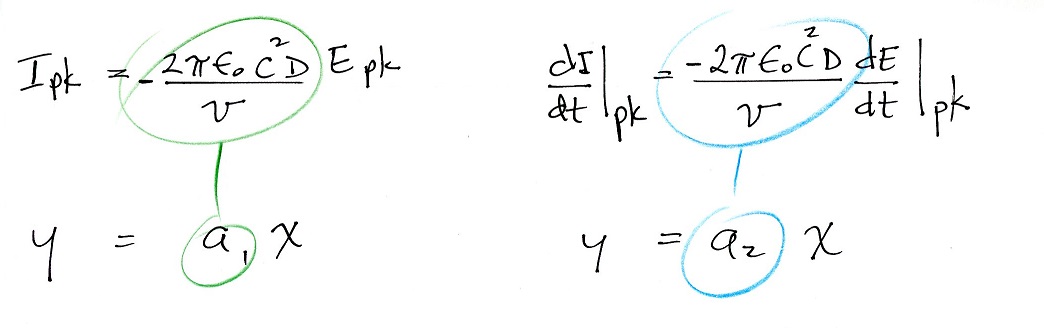You couldn't ask for a simpler relationship between Erad and I (or dErad/dt and dI/dt).
 Erad has the same shape as the current waveform measured at the ground.  Ditto for dErad/dt and dI/dt.

These expressions are widely used to estimate Ipeak and peak values of dI/dt from measured Erad and dErad/dt.

Note that both peak I and peak dI/dt occur when the tip of the upward moving return stroke current waveform is close to the ground.  The assumption that the return stroke channel is straight and vertical might not be too bad at this point.  The assumption that sin θ   = 1 is also satisfied

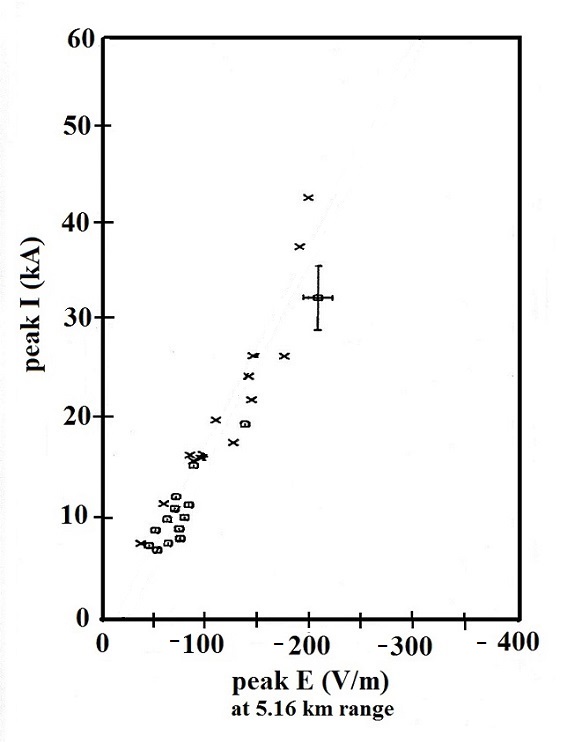
The discussion of lightning return stroke current models was interrupted at this point to take a look at HW#6 pt. 1.  The assignment deals with the data shown in the figure below:




The figure at left shown 28 simultaneous measurements of peak I and peak E.  Measurements of peak dI/dt and peak dE/dt for the same 28 discharges are shown at right.
The I and dI/dt data were measured in subsequent return stroke discharges triggered at the Kennedy Space Center.  The E and dE/dt data were measured at a location 5.16 km away.  The data are from Willett et al. (1989), a full citation and a link to the report can be found at the end of today's notes.  You'll also find more information about the experiment in the Supplementary Reading section "An experimental test of the transmission-line model."

The fact that the points appear to be linearly distributed would seem to confirm that TL model prediction of a direct proportionality between Ipk and Epk (also [dI/dt]pk and [dE/dt]pk).  In the assignment you are first supposed to fit a straight line to both sets of data.  The line should be constrained to pass through the origin, thus a line y = ax rather than y = ax + b (some additional information about how to do this is included on the assignment).

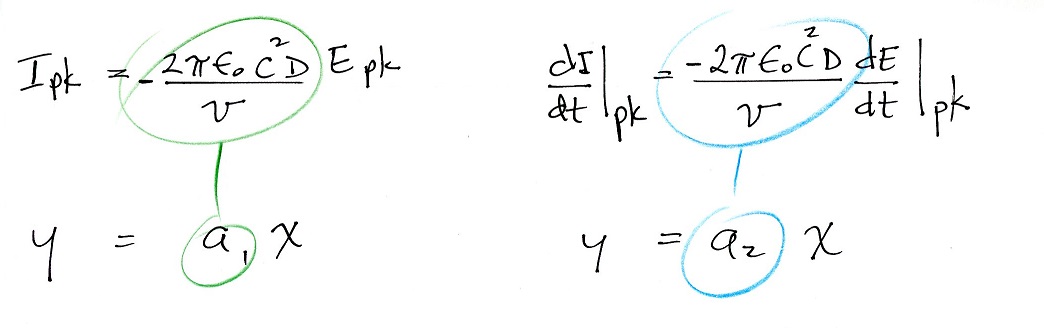
The TL model predicts that you should end up with the same value of a for both data sets (i.e. a1 and a2 should be equal).  I hinted that might not be the case.  Once you have a value for a you need to determine the value of the return stroke velocity, v.

We'll pretty much be limiting our attention to the transmission-line model from this point onward.  Nonetheless there is one additional model that should be mentioned before we finish this section.

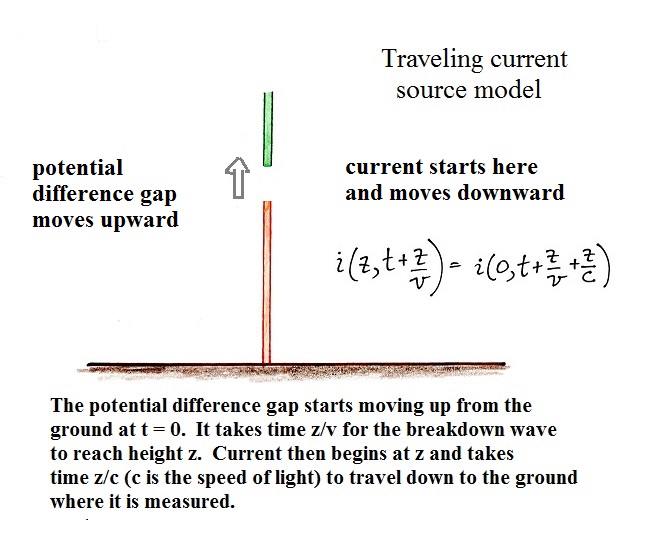
Traveling current source (TCS) model

The TL model is probably the easiest to visualize.  You inject a current signal into the lightning channel at ground level and the signal propagates up the channel at constant speed without any change in shape.  In the TCS model currents don't begin at the ground and travel upward, currents begin above the ground and travel downward. 

The TCS model is harder (for me at least) to visualize.  In this model (originally proposed by Heidler (1985)) current at some level above the ground doesn't start until the potential difference gap separating cloud and ground potential (separating the bottom of the leader from the top of the upward moving return stroke channel) has reached that level.  That takes time t = z/v.  Then charge surrounding the leader core flows into the return stroke channel and then travels downward to the ground (at the speed of light) where it is measured. 



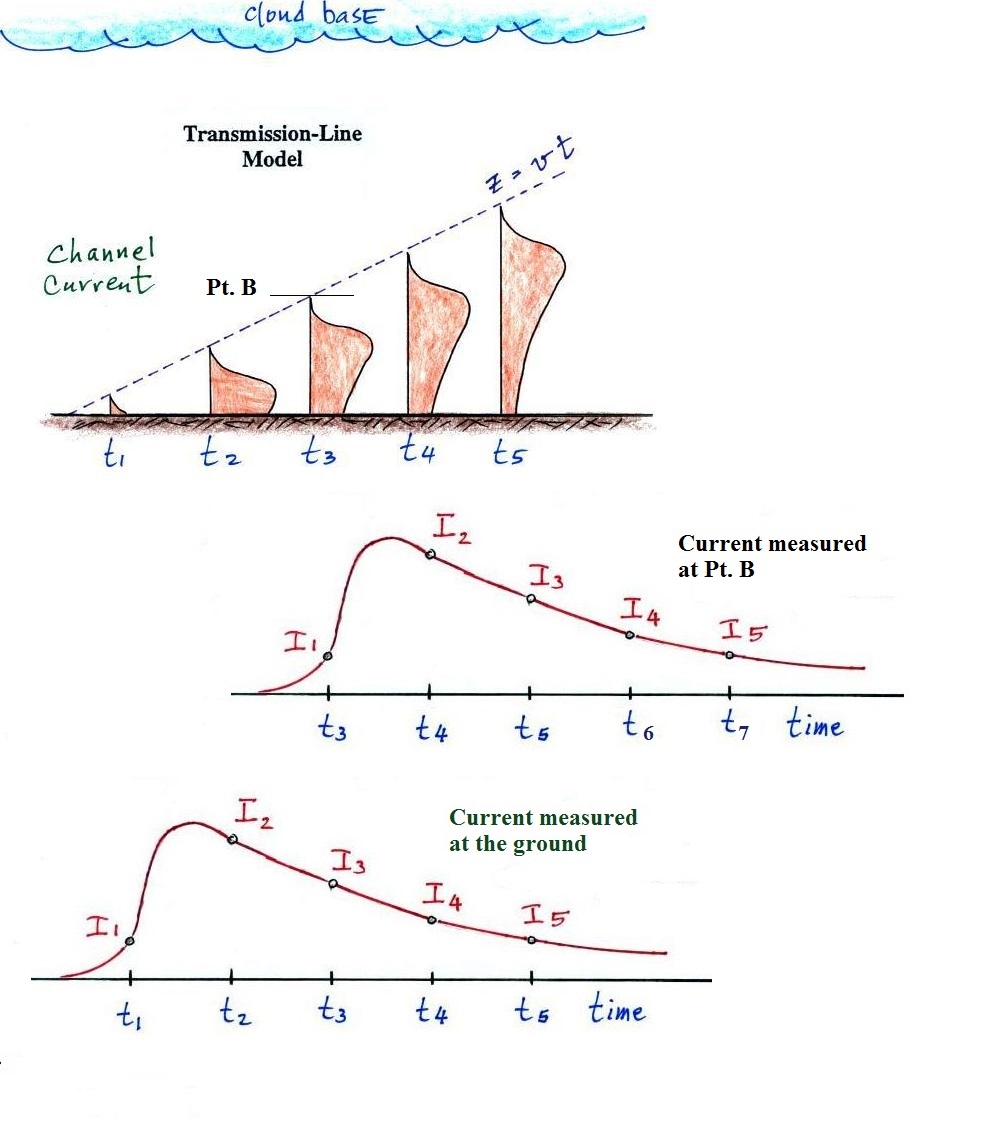
We can also show a diagram of the current waveforms that would be seen at different levels above the ground and also how currents vary along the channel at different times.
























Note that current waveform at a given level above the ground begins discontinuously (instantaneously).  This presents a problem when computing the E and B fields because dI/dt is infinite.  The Diendorfer-Uman model (DU) modifies the TCS model and turns the current on more gradually.  I mention this here because you'll see the DU model in a list that ranks the various models later in these notes.

We won't discuss the TCS model further at this point.  However there is an interesting result from this model that we will refer to in the next class or two.

Testing and validating the current models
We had run out of time at this point, so I've moved the material in this last section to the next class. 

 
References:

C.E.R. Bruce, R.M. Golde, "The Lightning Discharge," J. Inst. Electr. Eng., 88, 487-520.

F. Heidler, "Traveling current source model for LEMP calculation, Proc. 6th Symposium on EMC, Ed. by T. Dvorak, Zurich, Switzerland, 1985.

P.F. Little, "Transmission Line Model of a Lightning Return Stroke," J. of Physics D: Applied Physics, 11, 1893-1910, 1978

C.A. Nucci, G. Diendorfer, M.A. Uman, F. Rachidi, M. Ianoz, and C. Mazzetti, "Lightning Return Strok,e Current Models With Specified Channel-Base Current: A Review and Comparison," J. Geophys. Res., 95, 20395-20408, 1990.

M.N. Plooster, "Numerical Simulations of Spark Discharges in Air," Physics of Fluids, 14, 2111-2123, 1971.

M.N. Plooster, "Numerical Model of the Return Stroke of the Lightning Discharge," Physics of Fluids, 13, 2124-2133, 1971.

G.H. Price and E. T. Pierce, "The modeling of channel current in the lightning return stroke," Radio Sci., 12, 381-388, 1977.

V.A. Rakov and M.A. Uman, "Review and Evaluation of Lightning Return Stroke Models Including Some Aspects of Their Application," IEEE Trans. on EMC, 40, 403-426, 1998.

V.A. Rakov, "Fundamentals of Lightning", Cambridge Univ. Press, 2016

J.C. Willett, J.C. Bailey, V.P. Idone, A. Eybert-Berard, and L. Barrett, "Submicrosecond Intercomparison of Radiation Fields and Currents in Triggered Lightning Return Strokes Based on the Transmission-Line Model," J. Geophys. Res., 94, 13275-13286, 1989.