Tue., Oct. 17 notes

Tuesday Oct. 17, 2006

Quiz #2 was returned in class today. The average grade was 70%. Be sure to carefully check the grading on your quiz.

The Experiment #2 reports have been graded and were returned in class. You have two weeks to revise your report. Revised reports are due in two weeks on Tue., Oct. 31. Please return the original report with your revised report.

A few remaining sets of Experiment #3 materials are still available for checkout.

The 1S1P Assignment #2a reports are due Thursday this week (Oct. 19). The Assignment #2b reports are due next Tuesday (Oct. 24). The Surface Weather Map Analysis worksheet is now available.

Coming on Thursday: two new optional assignments.
Coming next week: Experiment #4

Now we move to an important new topic: humidity. The beginning of Chapter 4 can be a little overwhelming and confusing. If you find it too confusing, I would suggest you stop reading and not worry too much about it. Study the class notes and once you feel comfortable with the material there you can go back and read the beginning of Chapter 4.

A brief introduction to some of the humidity variables is given on p. 83 in the photocopied notes. We will be mainly interested in 4 variables: mixing ratio, saturation mixing ratio, relative humidity, and dew point.

Mixing ratio tells you how much water vapor is actually in the air. Mixing ratio has units of grams of water vapor per kilogram of dry air (how much water vapor in grams is mixed with a kilogram of dry air). It is basically the same idea as teaspoons of sugar mixed in a cup of tea.

Saturation mixing ratio is just an upper limit to how much water vapor can be found in air. It doesn't say anything about how much water vapor is actually in the air (that's the mixing ratio's job). Warm air can potentially hold more water vapor than cold air. This variable has the same units: grams of water vapor per kilogram of dry air.

The dependence of saturation mixing ratio on air temperature is illustrated below:

The small specks represent all of the gases in air except for the water vapor. Each of the open circles represents 1 gram of water vapor that the air could hold. There are 15 open circles drawn in the 1 kg of 70 F air; each 1 kg of 70 F air could hold up to 15 grams of water vapor. The 40 F air only has 5 open circles; this cooler air can only hold up to 5 grams of water vapor per kilogram of dry air.

Now we have gone and actually put some water vapor into the volumes of 70 F and 40 F air. 3 grams of water vapor have been added to each volume of air. The mixing ratio, r, is 3 g/kg.

The relative humidity tells you how "full" the air is with water vapor. If you think of the student/classroom analogy, a classroom with 16 seats (analogous to the saturation mixing ratio) contains 4 students (analogous to the mixing ratio). The classroom would be 25% full.

Here are the relative humidities of the 70 F and 40 F air that each contain 3 grams of water vapor. The 70 F air has a low RH because this warm air's saturation mixing ratio is large. The RH in the 40 F is higher even though it has the same actual amount of water vapor because the 40 F air can't hold as much water vapor and is closer to being saturated.

You can see how RH doesn't really tell you how much water vapor is actually in the air. The two volumes of air above contain the same amount of water vapor (3 grams per kilogram) but have different relative humidities.

The dew point temperature has two jobs. First it is a measure of the actual amount of water vapor in the air. In this respect it is just like the mixing ratio. If the dew point temperature is low the air doesn't contain much water vapor. If it is high the air contains more water vapor.

Second the dew point tells you how much you must cool the air in order to cause the RH to increase to 100% (at which point a cloud, or dew or frost, or fog would form).

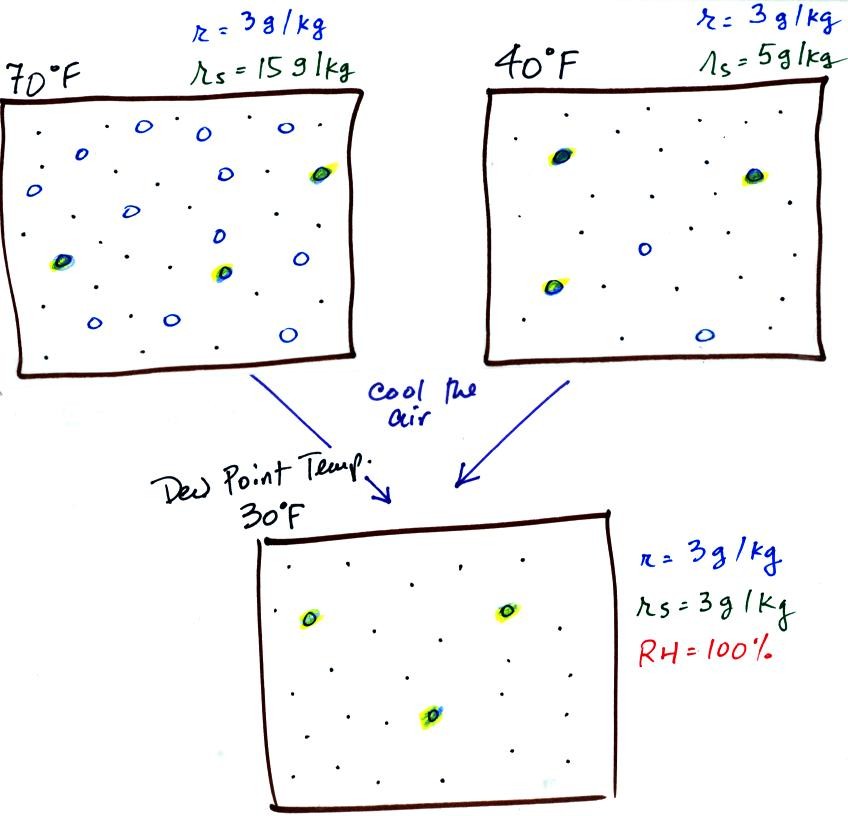
If we cool the 70 F air or the 40 F air to 30 F we would find that the saturation mixing ratio would decrease to 3 grams/kilogram. Since the air actually contains 3 g/kg, the RH of the 30 F air would become 100%. The 30 F air would be saturated, it would be filled to capacity with water vapor. 30 F is the dew point temperature for 70 F air that contains 3 grams of water vapor per kilogram of dry air. It is also the dew point temperature for 40 F air that contains 3 grams of water vapor per kilogram of dry air.

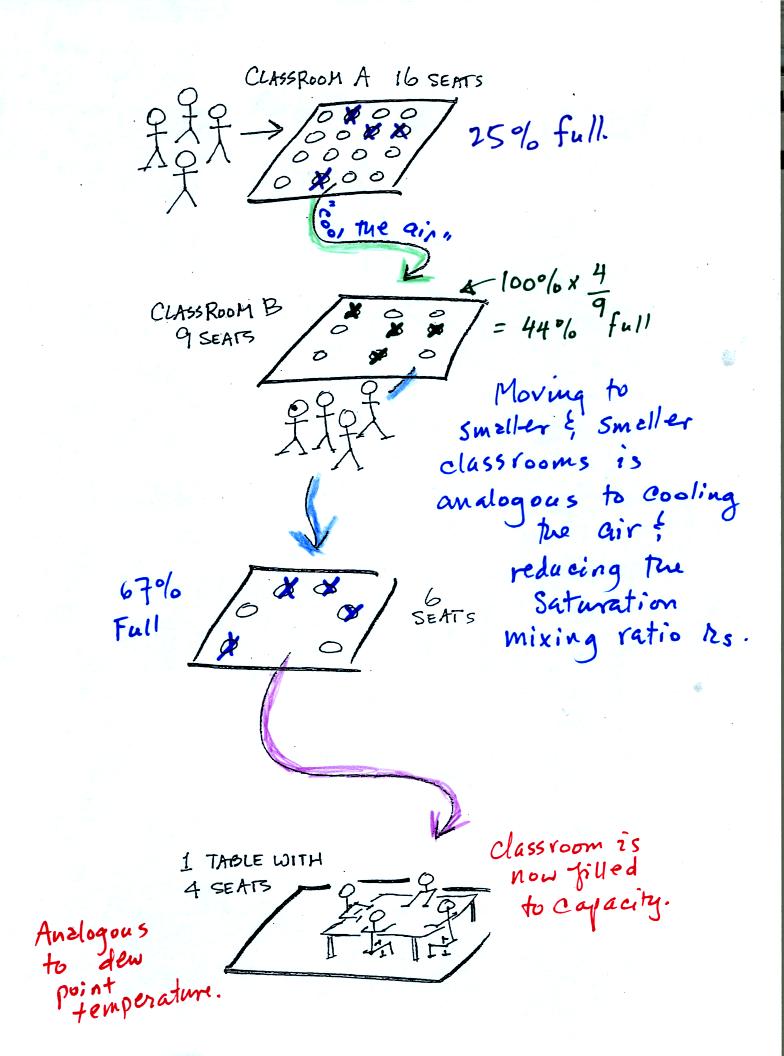
Now back to the students and classrooms analogy on the righthand side of p. 83. The 4 students move into classrooms of smaller and smaller capacity. The decreasing capacity of the classrooms is analogous to the decrease in saturation mixing ratio that occurs when you cool air. Eventually the students move into a classroom that they just fill to capacity. This is analogous to cooling the air to the dew point temperature, at which point the RH becomes 100% and the air is filled to capacity, the air is saturated with water vapor.

The number of students is analogous to the mixing ratio
The classroom capacity is analogous to the saturation mixing ratio
The relative humidity is analogous to how full a classroom is
Moving from smaller and smaller rooms until the students just fill a room is analogous to cooling the air to the dew point temperature.

Next we will try to understand better why it is possible to saturate air with water vapor. Why is there an upper limit to the amount of water vapor that air can contain? Why does this upper limit depend on air temperature?

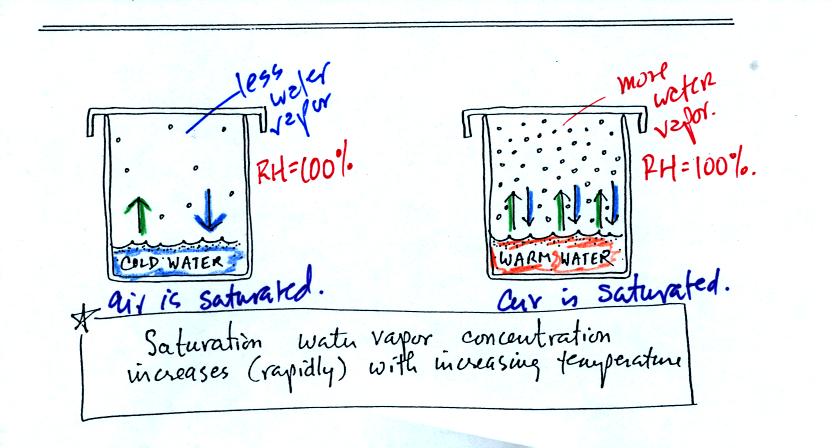
First we need to understand that the rate at which water evaporates depends on the water's temperature.

To be able to evaporate a water molecule must make its way up to the surface of the water and the water molecule must have sufficient energy to overcome any attractive forces trying to keep it in a liquid state. In cold water only a limited number of the water molecules have the necessary energy - cold water has a low rate of evaporation. In hot water, a larger fracton of the water molecules will have enough energy, hot water evaporates more rapidly.

In many respects this is like a grade distribution for a class.

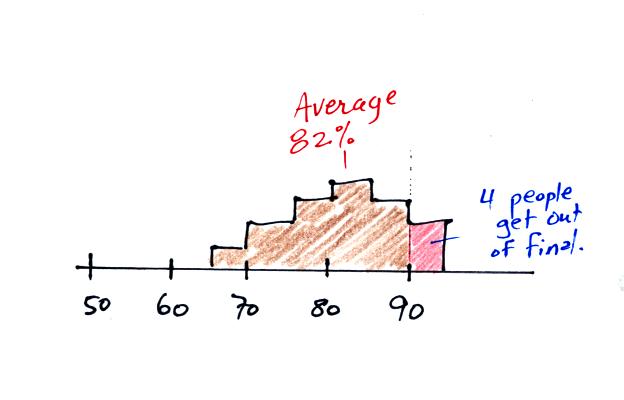
The 4 people that don't have to take the final exam in the example above (because they have an average grade of 90.0% or above) is analogous to the water molecules that have enough energy to evaporate.
If we were to add 5% points to the grade of everyone in the class, the class average would increase. This would be like warming some water. The increase in water temperature would be telling you that the average kinetic energy of the water molecules had increased.
Adding 5% to everyone's grade would also mean that more students wouldn't have to take the final exam. In the case of the water, more water molecules would have the kinetic energy needed to evaporate.

Now we will look at the top part of p. 85 in the photocopied notes. We have put a cover on the glass of room temperature water.

In #1 we see that the water is evaporating (2 arrows worth of evaporation). Water vapor will begin to build up in the air in the glass. This is shown in #2. Some of the water vapor molecules will condense (even though they may have just evaporated). In Fig. #3 the amount of water vapor has built up to a point where there is one arrow worth of condensation. In #3 there is still more evaporation than condensation so the water vapor concentration will increase a little bit more. Eventually in #4 the water vapor concentration has increased to a point that there are two arrows of condensation. This balances the 2 arrows of evaporation. The air is saturated, the air is filled to capacity. The amount of water vapor in the air will remain constant.

What would happen if we took off the cover and added some more water vapor to the glass in Fig. #4? This is the question that I told you think about and mentioned that I would put the answer in the online notes. The figure below wasn't shown in class.

The air in Fig. #5 shows what would happen. The air would be supersaturated with water vapor and the RH would be greater than 100%. This is possible but it is not an equilibrium situation. The increased amount of water vapor would increase the rate of condensation. There would be more condensation than evaporation. The water vapor concentration would begin to decrease. Eventually the glass would end back at the equilibrium situation in Fig. #4.

If we look at the bottom of p. 85 we see that the air in all three cases is saturated (equal rates of evaporation and condensation in each case). The relative humidity is 100% in all three cases. The amount of water vapor in the air however is different. The warm air contains a lot more water vapor than the cold air.

This information is on p. 86 in the photocopied class notes.

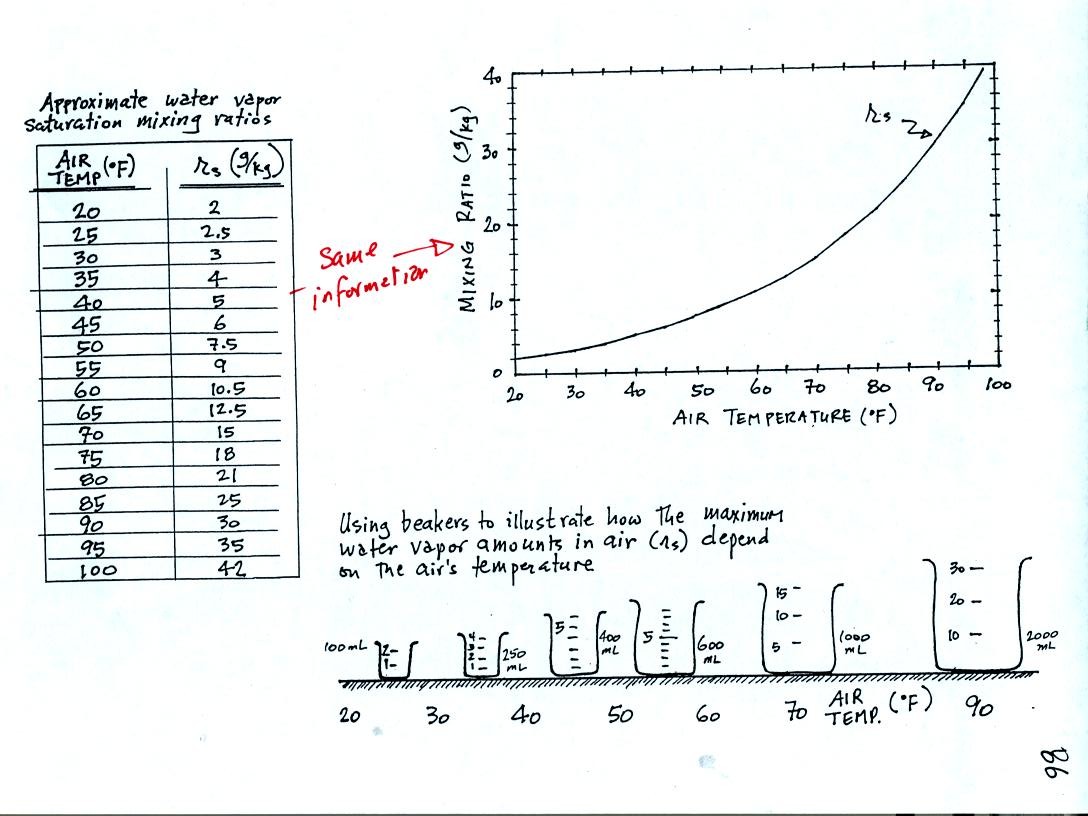
This page just gives you saturation mixing ratio values as a function of air temperature. The data are listed in a table and plotted on a graph.

The beakers are meant to show graphically the relative amounts of water vapor that air at different temperatures can contain. Don't get the idea that you could evaporate 2 L of water into a kilogram of 90 F air. The 90 F air couldn't contain anywhere near that much water vapor. What the 90 F beaker does show is that 90 F air can contain twice as much water vapor as 70 F air.

Now we'll work a series of humidity problems. By doing this you should begin to get a better feeling for what the various humidity variables are and how they work. Pay particular attention to what causes them to change.

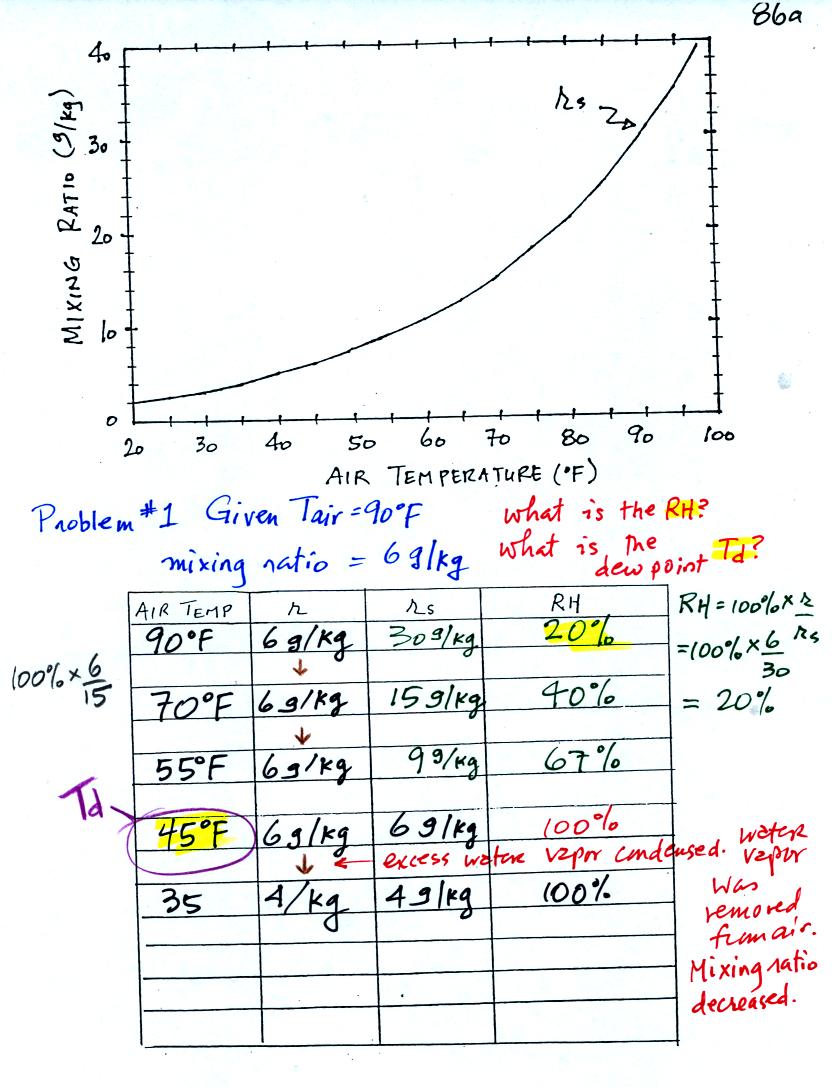
Here is the first sample problem that we worked in class. You might have a hard time unscrambling this if you're seeing it for the first time. The series of steps that we followed are retraced below:

We're given an air temperature of 90 F and a mixing ratio (r) of 6 g/kg. We're first supposed to find the relative humidity (RH).

We start by entering the data we were given in the table. Once you know the air's temperature you can look up the saturation mixing ratio value; it is 30 g/kg for 90 F air. 90 F air could potentially hold 30 grams of water vapor per kilogram of dry air (it actually contains 6 grams per kilogram in this example).

Once you know mixing ratio and saturation mixing ratio you can calculate the relative humidity.

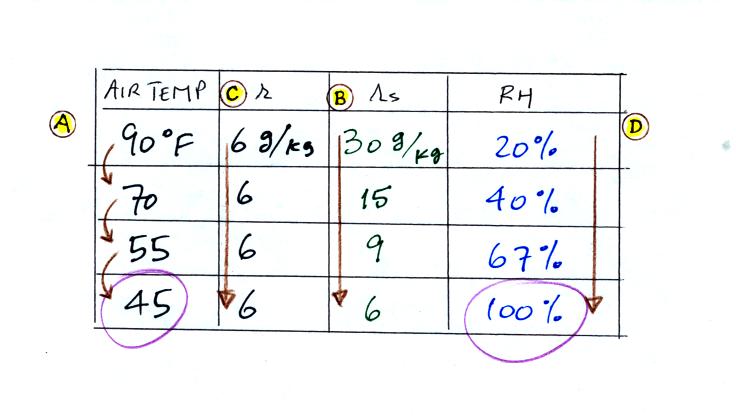
The numbers we just figured out are shown on the top line above.

(A) We imagined cooling the air from 90F to 70F, then to 55F, and finally to 45F.

(B) At each step we looked up the saturation mixing ratio and entered it on the chart. Note that the saturation mixing ratio values decrease as the air is cooling.

(C) The mixing ratio doesn't change as we cool the air. The only thing that changes r is adding or removing water vapor and we are doing neither.

(D) Note how the relative humidity is increasing as we cool the air. The air still contains the same amount of water vapor it is just that the air capacity is decreasing.

Finally at 45 F the RH becomes 100%. The dew point temperature in this problem is 45 F.

What would happen if we cooled the air further still, below the dew point temperature.

35 F air can't hold the 6 grams of water vapor that 45 F air can. You can only "fit" 4 grams of water vapor into the 35 F air. The remaining 2 grams would condense. If this happened at ground level the ground would get wet with dew. If it happens above the ground, the water vapor condenses onto small particles in the air and forms fog or a cloud. Now because water vapor is being taken out of the air (and turned into water), the mixing ratio will decrease from 6 to 4.

In many ways this is liking squeezing a moist sponge (squeezing the sponge and reducing its volume is like cooling moist air and reducing the saturation mixing ratio). At first when you sqeeze the sponge nothing happens, no water drips out. Eventually you get to a point where the sponge is saturated. This is like reaching the dew point. If you squeeze the sponge any further (or cool air below the dew point) water will begin to drip out.

The second problem is shown above. Given an air temperature of 90 F and a relative humidity of 50% you are supposed to figure out the mixing ratio (15 g/kg) and the dew point temperature (70 F). The problem is worked out in detail below.

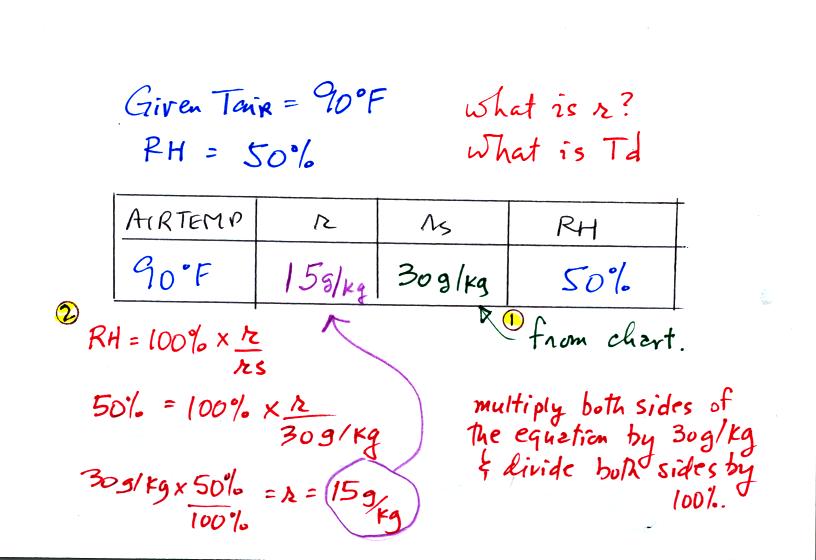
First you fill in the air temperature and the RH data that you are given. Since you know the air's temperature you can look up the saturation mixing ratio (30 g/kg). Then you can substitute into the relative humidity formula and solve for the mixing ratio (15 g/kg).

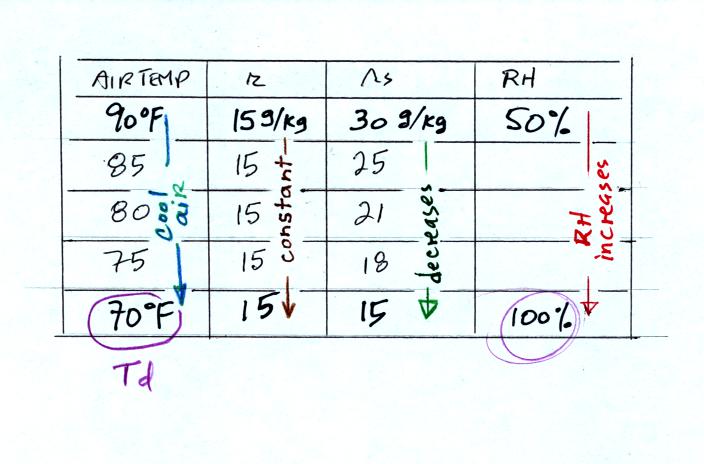
Finally you imagine cooling the air. Cooling causes the saturation mixing ratio to decrease, the mixing ratio stays constant, and the relative humidity increases. In this example the RH reached 100% when the air had cooled to 70 F. That is the dew point temperature.

There's something more you can learn from these two examples.

In the first example the RH was low and the difference between the air and dew point temperatures was large. In the second example, the RH was higher and the difference between the air and dew point temperatures was smaller. If there were no difference between the air and dew point temperature the RH would be 100%.

Can't wait until Thursday to see the remaining two humidity questions? Check the Thursday Oct. 19 notes.

This final portion of the online notes was a brief introduction to Experiment #3.

The two collectors below have been placed outside in the sunlight. They have been tilted at just the right angle so that the rays of sunlight strike them directly.

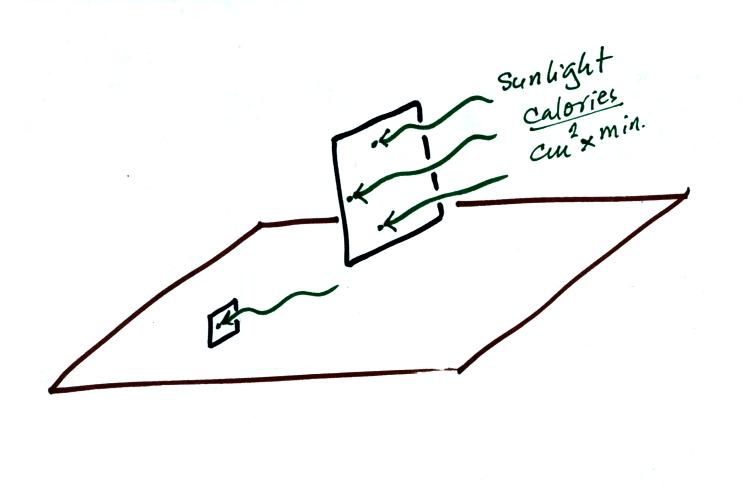
What does your intuition tell you? Would the larger collector absorb MORE energy than, LESS energy than, or the SAME amount of energy as the smaller collector?

What about the following situation? Two collectors with the same crossectional area are left out in the sun for different amounts of time.

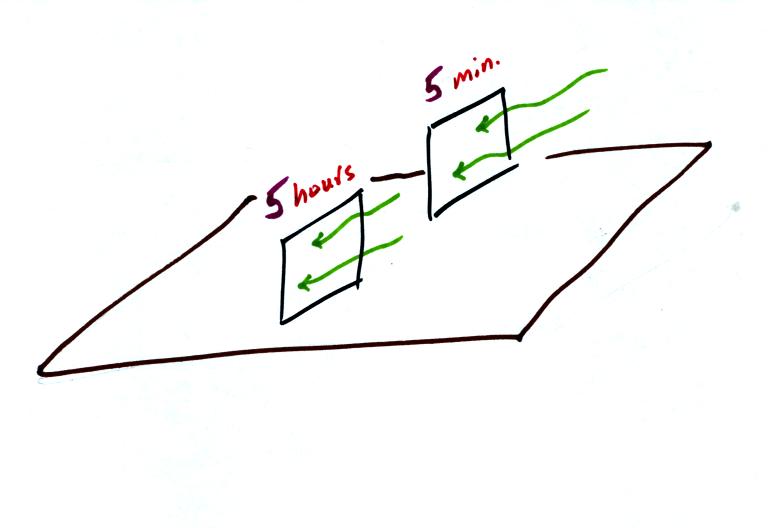
Will the collector that is left out for only 5 minutes absorb the same total amount of energy as the collector that is left in the sun for 5 hours? No, the collector left out for 5 hours will absorb a lot more energy than the collector left out for 5 minutes.

The energy absorbed by a collector will depend on the intensity of the sunlight, the area of the collector, and the amount of time the collector is left in the sun.

The variable S is the intensity of sunlight term. It is called solar irradiance and has units of calories per cm² per minute. That is what the people doing Experiment #3 are trying to measure.

A collector that starts to absorb energy will heat up (think of your car left out in the sun).

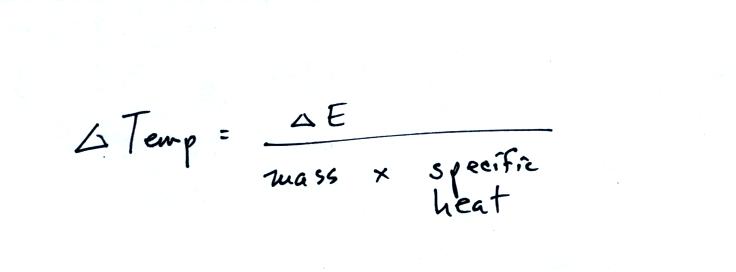
Here's that equation again. Now replace the energy term in this equation with the energy term from the other equation.

You can either measure or look up every term in this equation except for S.

The object of the solar irradiance experiment is to measure the solar irradiance, i.e. the energy in sunlight. You place a small block of aluminum outside in the sun and measure how quickly it warms up. You are given values for the mass and specific heat of the block and you can easily measure it's area.