Thursday Sept. 13, 2007
The Optional Assignment was collected today. They will be
returned in class next Tuesday. Answers to the questions should
appear online late Friday afternoon.
The Experiment #1 reports are due next Tuesday. If you haven't returned your materials you will
need to bring them by PAS 588. The graduated cylinders will be
needed by the students performing Experiment #2.
The Experiment #2 materials should be available in class next Thursday
(Sept. 20).
The 1S1P Assignment #1 reports are due next Tuesday.
The Quiz #1 Study Guide is now available
online. Quiz #1 will cover material on the Quiz #1 and Practice
Quiz Study Guides.
Isobars,
contours of pressure, drawn on a surface weather map reveal the large
scale pressure pattern. Winds spin counterclockwise (N.
Hemisphere) and converge into surface centers of low pressure.
This produces rising air motions which which cools the air and may
cause clouds to form.
Winds spin clockwise and diverge outward from centers of high
pressure. This results in sinking air motions and clear skies.
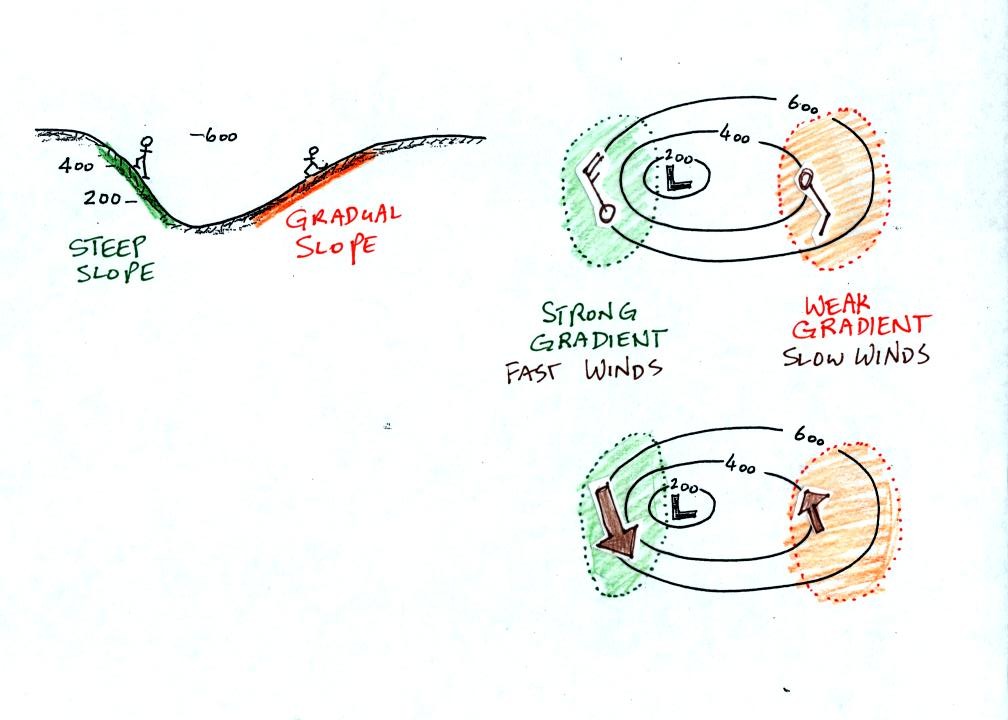
The pressure pattern can also tell you something about wind
speed. In this case we look for regions where
the isobars are either closely spaced together or widely spaced.
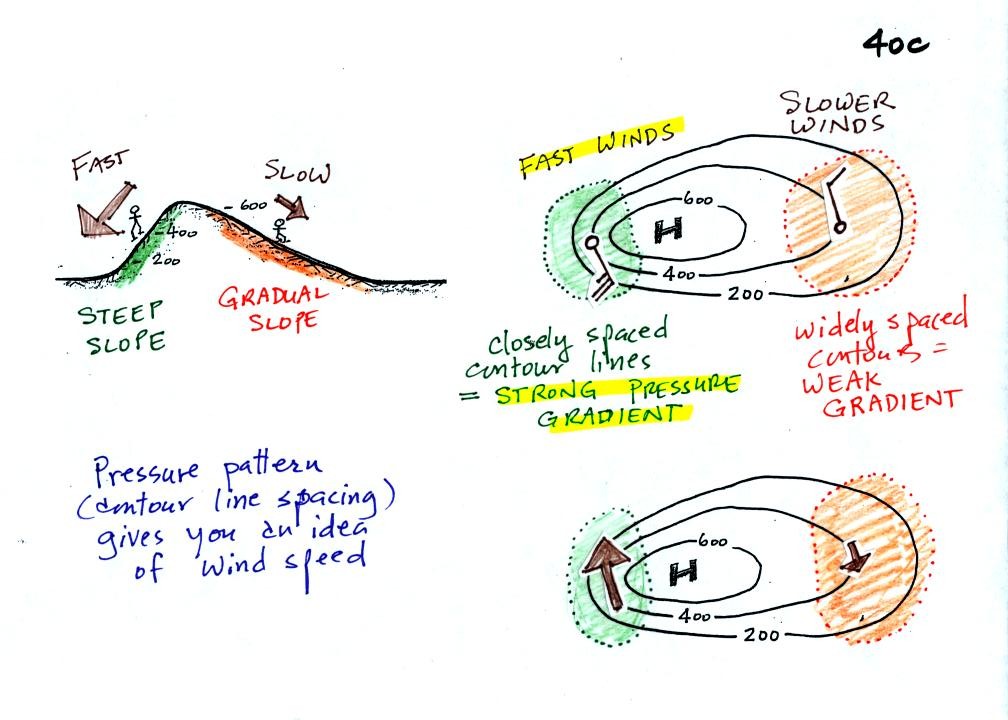
Closely spaced contours means pressure is changing rapidly
with
distance. This is known as a strong pressure gradient and
produces fast winds. It is analogous to a steep slope on a
hillside. If you trip, you will tumble rapidly down a steep
hillside, more slowly down a gradual slope.
The winds around a high pressure center are shown above using both the
station model notation and arrows. The winds are spinning clockwise and
spiralling inward slightly.
Winds spin counterclockwise and spiral inward around low
pressure
centers.
Try to determine the directions of the winds at Points 1, 2, and 3 in
the figure below (found at the bottom of p. 40c in the photocopied
Class Notes). Where will the fastest and slowest winds be
found? Would you expect to find that the temperatures at Points
1, 2, and 3 were equal or different?
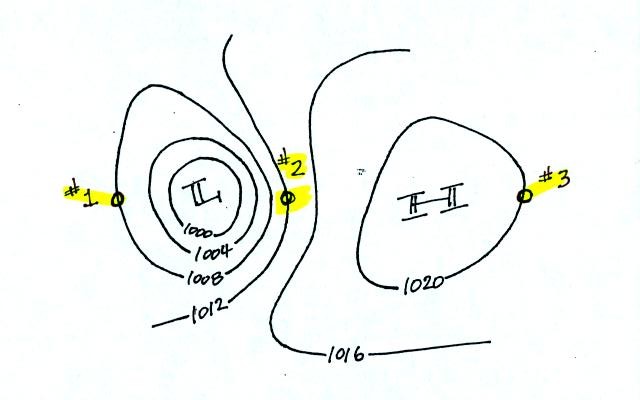
When you have thought about these questions for awhile,
click here to see the answers.
Once the
pressure pattern gets the wind blowing, the winds can change
the temperature pattern. The figure below shows the
temperature pattern you would
expect to see if the wind wasn't blowing at all or if the wind was
blowing straight from west to east. The bands of different
temperature are aligned parallel to the lines of latitude.
Temperature changes from south to north but not from west to east
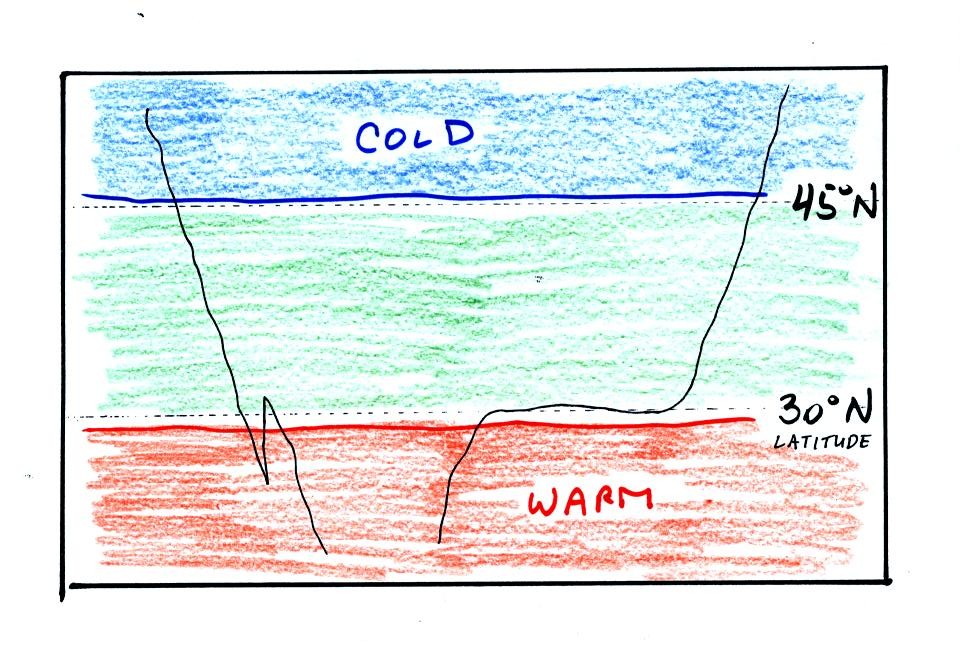
This isn't a very interesting picture (except for the
fact that the state of Florida is missing). It gets a
little
more interesting if you put centers of high or low pressure on the map.
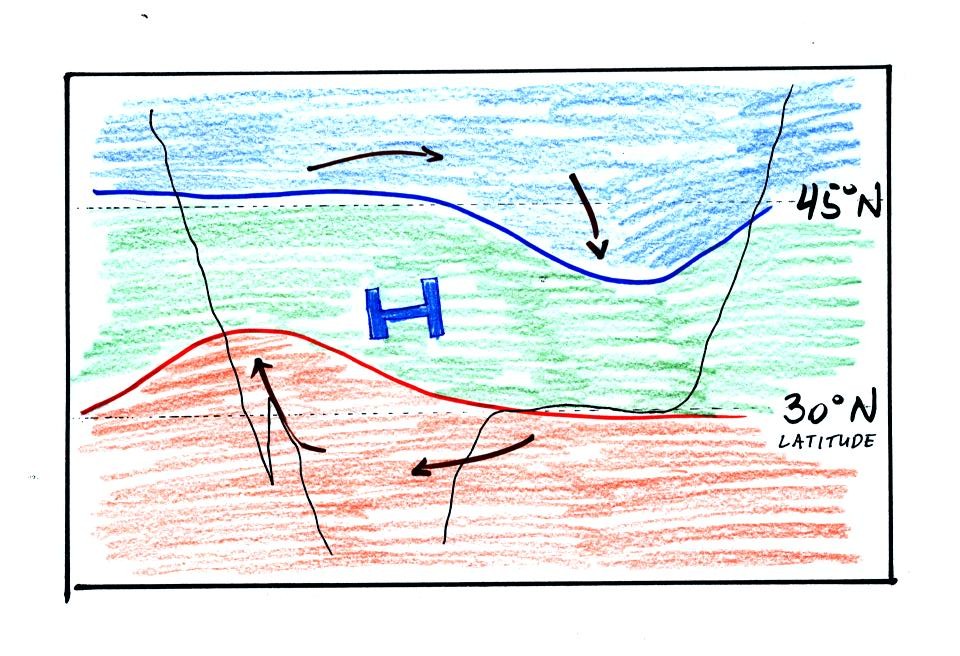
The clockwise spinning winds move warm air to
the north on
the western
side of the High. Cold air moves toward the south on the eastern
side of the High. The diverging winds also move the warm and cold
air away from the center of the High.
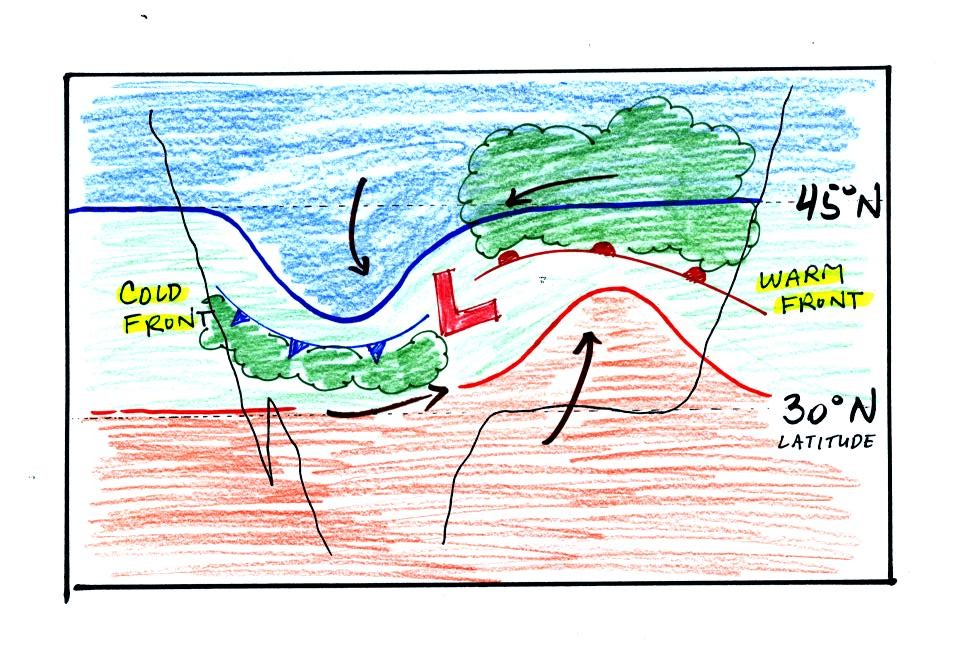
Counterclockwise winds move cold air toward the south on the
west side
of the Low. Warm air advances toward the north on the eastern
side of the low.
The converging winds in the case of low pressure will move the air
masses of different temperature in toward the center of low pressure
and cause them to collide with each other. The boundaries between
these colliding air masses are called fronts. Fronts are a second
way of causing rising air motions (which is important because rising
air expands and cools and, if the
air is moist, clouds can form)
Cold air is moving from north toward the south on the
western side of
the low. The leading edge of the advancing cold air mass is a
cold front. Cold fronts are drawn in blue on weather maps.
The small triangular symbols on the side of the front identify it as a
cold front and show what direction it is moving. The fronts are
like spokes on a wheel. The "spokes" will spin counterclockwise
around the low pressure center.
A warm front (drawn in red with half circle symbols) is shown on the
right hand side of the map at the advancing edge of warm air. It
is also rotating counterclockwise around the Low.
Clouds can form along fronts (often in a fairly narrow band along a
cold front and over a larger area ahead of a warm front). We need
to look at the crossectional structure of warm and cold fronts to
understand better why this is the case.
This type of storm system is referred to as an extratropical cyclone
(extra tropical means outside the tropics, cyclone means winds spinning
around low pressure) or a middle latitude storm. Large
storms also form in the tropics, they're called tropical cyclones or
more commonly hurricanes.
The top picture below shows a crossectional
view of a cold front
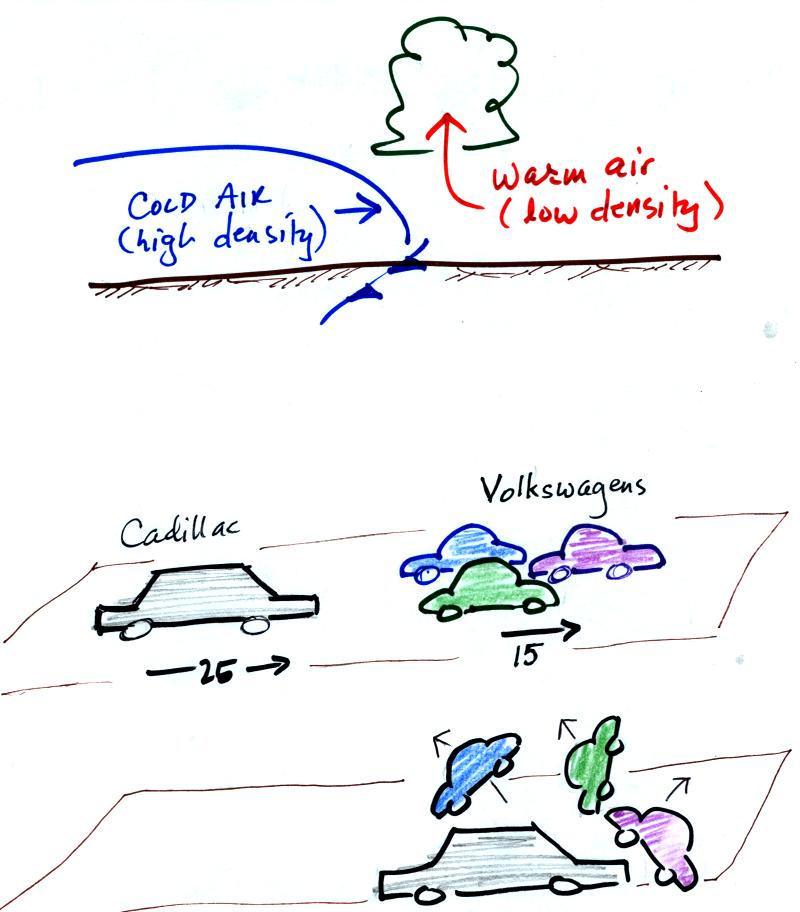
At the top of the figure, cold dense air on the left is advancing
into
warmer lower density air
on the right. We are looking at the front edge of the cold air
mass. The warm low density air is lifted out of the way
by the cold air.
The lower figure shows an analogous situation, a big heavy Cadillac
plowing into a bunch of
Volkswagens. The VWs are thrown up into the air by the Cadillac.
Here's a crossectional view of a warm front, the structure is a
little different.
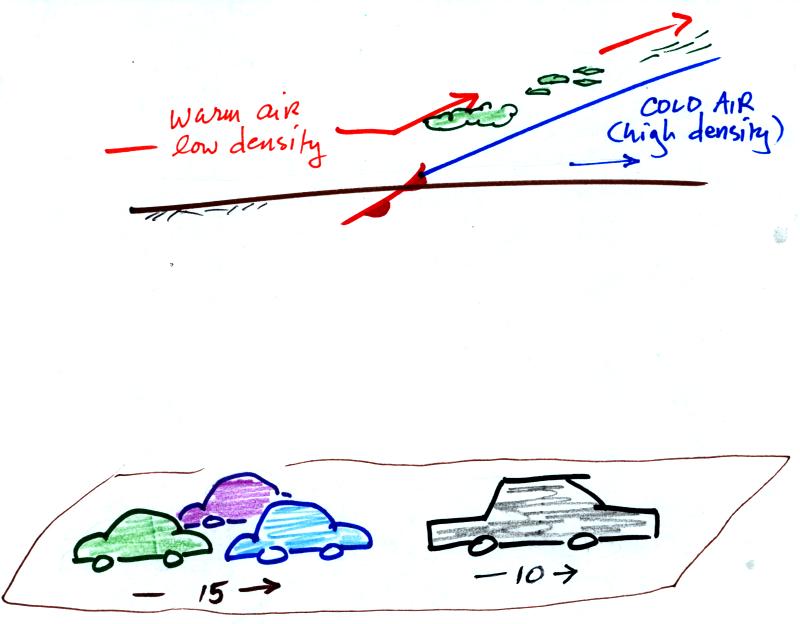
In the case of a warm front we are looking at the
back,
trailing edge of cold air (moving slowly to the right). Note the
ramp
like shape of the cold air mass. Warm air overtakes the cold
air. The warm air is still less dense than the cold air, it can't
wedge its way underneath the cold air. Rather the warm air
overruns the cold air. The warm air rises again (more gradually)
and clouds form. The clouds generally are spread out over a
larger area than with cold fronts.
In the automobile analogy, the VWs are catching a Cadillac. What
happens
when they overtake the Cadillac?

The Volkswagens aren't heavy enough to
lift the
Cadillac.
They run up and over the Cadillac.
Now we will return to the
surface weather map we have been analyzing.
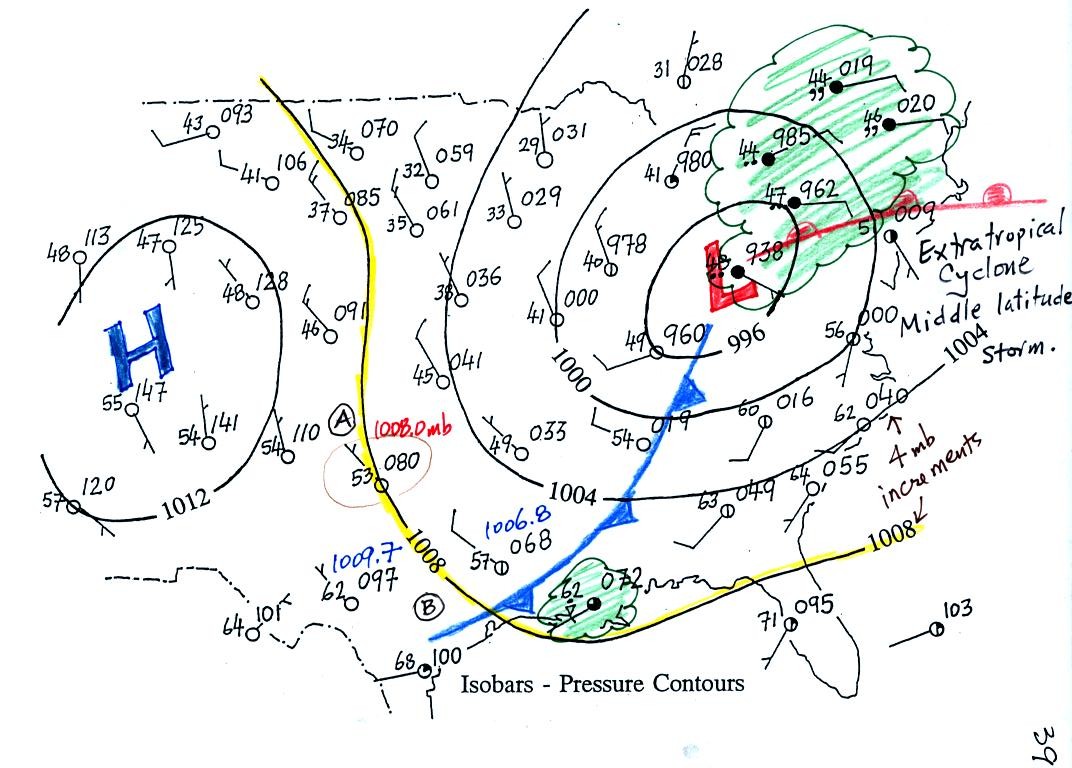
The weather data plotted on the map indicate clearly the presence of
cold and a
warm fronts (we learn later about some of the criteria used to located
fronts). Now we can begin to understand what is causing the rain
shower along the Gulf Coast (clouds caused by an approaching cold
front) and the cloudy rainy weather in the Northeast (convergence into
a low pressure center and an approaching warm front).
Toward the
end of class we returned to a topic introduced last Tuesday.
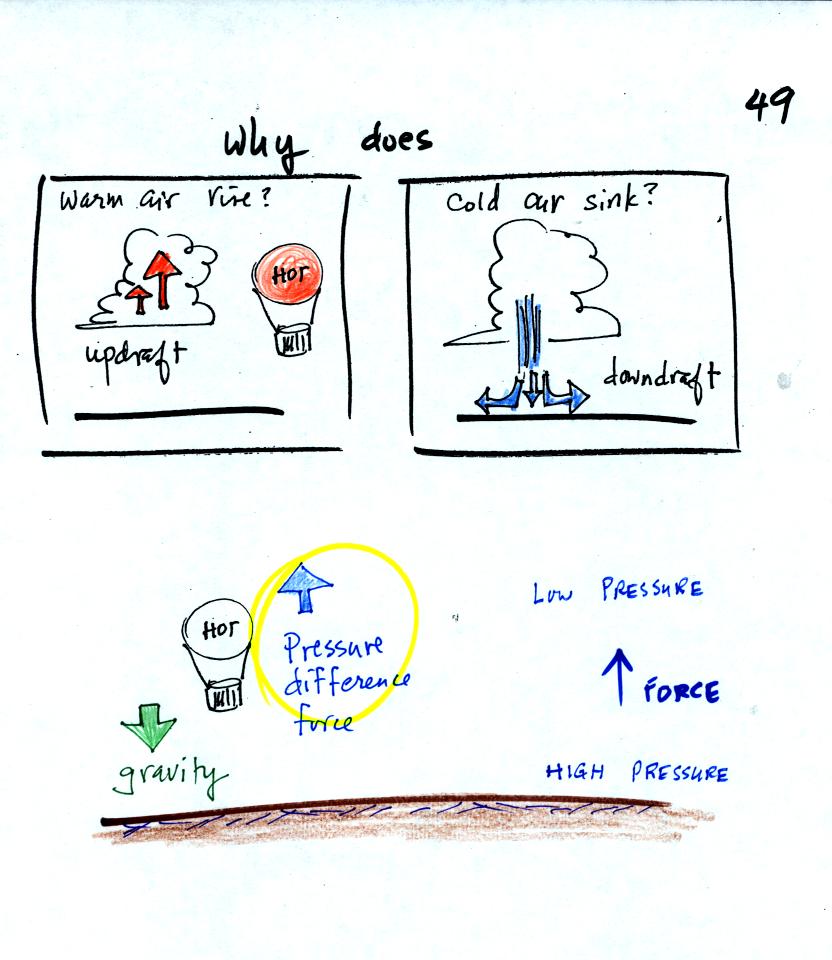
We are going to try to understand why warm air rises and
cold air sinks.
It is always a good idea to have a picture in mind, a hot air balloon
for example.
Hot air balloons do sometimes fall from the sky; most everyone in the
classroom would understand that gravity was the force responsible for
bringing down a hot air balloon.
But what causes a hot air balloon to rise? We will see that it is
a pressure difference force. Pressure decreases with increasing
altitude. This creates a force that points upward from high
toward low pressure.
Understanding rising and sinking air is a 3-step process. The
first step is learning about the ideal gas law.

Up to this point we have been thinking of pressure as being determined
by the weight of the air overhead. Air pressure pushes down
against the ground at sea level with 14.7 pounds of force per square
inch. We also learned that pressure pushes sideways and
upward. Air surrounding a balloon pushes against all the
sides of a balloon, but the air pressure doesn't crush the
balloon. Air inside the balloon pushes back with the same
force. The ideal gas law equation will give us an idea of what
determines the strength of the pressure inside the balloon.
So here
goes, we'll figure out what variables belong in the ideal gas law
equation and how they affect the pressure.

A. The pressure produced by the air
molecules inside a balloon will
first depend on how many air molecules are there. If there
weren't any air molecules at all there wouldn't be any
pressure. As you add more and more add to something like a
bicycle tire, the
pressure increases. Pressure is directly proportional to N - an
increase in N causes an increase in P. If N doubles, P also
doubles (as long as the other variables in the equation don't change).
B. Air pressure inside a balloon
also
depends on the size of the
balloon. Pressure is inversely proportional to volume, V
. If V were to double, P would drop to 1/2 its original value.
Note it is possible to keep pressure constant by changing N and V
together in just the right kind of way. This is what happens in
Experiment #1 that some of you are working on. Oxygen in a
graduated cylinder reacts with steel wool to form rust. Oxygen is
removed from the air sample which is a decrease in N. As oxygen
is removed, water rises up into the cylinder decreasing the air sample
volume. N and V both decrease in the same relative amounts and
the air sample pressure remains constant.
If you were to remove 1/2 of the air molecules, V would decrease
to 1/2 its original value and pressure would stay constant.

C. Increasing
the temperature of the gas in a balloon will cause the gas molecules to
move more quickly. They'll collide with the walls of the balloon
more frequently and rebound with greater force. Both will
increase the pressure.
You
shouldn't throw a can of spray paint into a fire (or even leave it
inside a hot car). The
pressure of the gas inside a container depends on the gas
temperature. If the can gets hot enough, the buildup in pressure
could cause the can to rupture.
D. Surprisingly the pressure
does
not depend on the mass of the
molecules. Pressure doesn't depend on the composition of the
gas. Gas molecules with a lot of mass will move slowly, the less
massive molecules will move more quickly. They both will collide
with the walls of the container with the same force.
The two ideal gas law equations are shown at the bottom of
the page above. You can
ignore the
constants k and R if you are just trying to understand how a change in
one of the variables would affect the pressure. You only need the
constants when you are doing a calculation involving numbers.
(1) Pressure = (Number of air molecules) multiplied by temperature divided by volume
or
(2) Pressure = (density) multiplied
by (temperature)
The Expt. #1 people will use Eqn. (1) in their reports. They
should be thinking about what variables in the equation remain constant
and which ones change.
Here is an ideal
gas law animation that wasn't shown in class.
You
can vary N, V, or T and see the effect on pressure.
We now
turn our attention to Charles' Law, a special situation involving the
ideal gas law

Air in the atmosphere behaves like air in a
balloon. A
balloon can grow or shrink in size depending on the pressure of the air
inside.
We start in the upper left hand corner with air inside a balloon that
is exactly the same as the air outside. The air inside and
outside have been colored green. The brown arrows show that the
pressure of the air inside pushing outward and the pressure of
the air surrounding the balloon pushing inward are all the same.
Next we warm the air in the balloon (Fig. 2). The ideal gas law
equation
tells us that the pressure of the air
in the balloon will increase. The increase is
momentary though.
Because the pressure inside is now greater than
the pressure outside, the balloon will expand. As volume begins
to increase, the pressure of the air inside the balloon will
decrease.
Eventually the balloon will expand just enough that the pressures
inside and
outside are again in balance. You end up with a balloon of warm
low density air that has the same pressure as the air surrounding it
(Fig. 3)
You can use the same reasoning to understand that cooling a balloon
will cause its volume to decrease. You will end up with a balloon
filled with cold high density air. The pressures inside and
outside the balloon will be the same.
These associations: warm air
= low density air and cold
air = high density air are important and
will come up a lot during the remainder of the semester.

Charles Law can be demonstrated by dipping a balloon in liquid
nitrogen. When you pull the balloon out of the liquid nitrogen it
is very small. It is filled with cold high density air. As
the balloon warms the balloon expands and the density of the air inside
the balloon decreases. You watch as air temperature and air
density (or
volume) inside the balloon change in a way that keeps the pressure
constant.















