Wednesday, September 11

We'll be using page 49, page 50, page 51, page 52, page 53 (the online version has been updated, I'll bring copies of the new page to class for students that bought the ClassNotes packet), page 54, page 54a, and page 54b from the ClassNotes today.

Trying to understand why warm air rises & cold air sinks
                                                        












Hot air balloons floating over the Rio Grande river during the 2013 Albuquerque Balloon Fiesta (source of the photo)
 Photograph of a microburst, a localized intense thunderstorm downdraft, that hit Wittmann Arizona in July 2015.  Surface winds of 55 MPH were measured. (source of the photo)
 Cold sinking air.  The air was cooled by coming into contact with a piece of dry ice. (image source)

A full understanding of these rising and sinking motions is a 3-step process (the following is found on page 49 in the photocopied ClassNotes).




We will first learn about the ideal gas law.  It's is an equation that tells you which properties of the air inside a balloon work to determine the air's pressure. 

Next we will look at Charles' Law, a special situation involving the ideal gas law (air temperature volume, and density change together in a way that keeps the pressure inside a balloon constant).  Then we'll learn about the 2 vertical forces that act on air.  I'm pretty sure you know what the downward force is and suspect that you don't recall what the upward force is (hint we talked about it in class on Tuesday ).

The ideal gas law - a microscopic scale explanation of air pressure




We've spent a fair amount of time learning about pressure.  We first began with the idea that pressure is determined by the weight of the air overhead.  Air pressure pushes down against the ground at sea level with 14.7 pounds of force per square inch.  That's a perfectly sound explanation.

We then went a bit further and tried to imagine the weight of the atmosphere pushing down on a balloon sitting on the ground.  If you actually do push on a balloon you realize that the air in the balloon pushes back (and sideways) with the same force.  Air pressure everywhere in the atmosphere pushes upwards, downwards, and sideways.

These are large scale, atmosphere size, ways of thinking about pressure.  Next we are going to forget the atmosphere and focus in on just the air in the balloon. This is more of a microscopic view of pressure.

Imagine filling a balloon with air.  If you could look inside which picture below would be more realistic?



The view on the left is incorrect. 
The air molecules do not fill the balloon and
do not take up all the available space. 


This is the correct representation. 
The air molecules are moving around at 100s of MPH
but actually take up little or no space in the balloon.




The air molecules are continually colliding with the walls of the balloon and pushing outward (this force divided by area is the pressure).  Wikipedia has a nice animation.  An individual molecule doesn't exert a very strong force, but there are so many molecules that the combined effect is significant.


We want to identify the properties or characteristics of the air inside the balloon that determine the pressure and then put them together into an equation called the ideal gas law.


The ideal gas law equation
You're not going to have to be able to figure out or remember the ideal gas law equation.  I'll give it to you.  Here is is:



You should know what the symbols in the equation represent.  Probably the most obvious variable is N the number of air molecules.  It's the motions of the air molecules that produce pressure.  No air molecules (N = 0) means no pressure.  The more air molecules there are the higher the pressure.

Number of gas molecules or atoms



Pressure (P) is directly proportional to Number of air molecules (N).  If N increases P increases and vice versa.



Here's an example.  You're adding air to a tire.  As you add more and more air to something like a bicycle tire, the pressure increases.  Pressure is directly proportional to N; an increase in N causes an increase in P.  If N doubles, P also doubles (as long as the other variables in the equation don't change).

Temperature
Here's what I think is the next most obvious variable.



You shouldn't throw a can of spray paint into a fire because the temperature will cause the pressure of the gas (propellant) inside the can to increase and the can could explode.  So T (temperature) belongs in the ideal gas law equation



Increasing the temperature of the gas in a balloon will cause the gas molecules to move more quickly (kind of like "Mexican jumping beans").  They'll collide with the walls of the balloon more frequently and rebound with greater force - that will increase the pressure.



We've gotten a little bit ahead of the story.  The variable V (volume) has appeared in the equation and it's in the denominator.  A metal can is rigid.  It's volume can't change (up until the moment the can explodes).  When we start talking about air in balloons or in the atmosphere volume can change.  A change in temperature or a change in number of air molecules might be accompanied by a change in volume.  Balloons and cans of spray paint are sealed, so N also stays constant.

At this point we did a quick demonstration to show the effect of temperature on the pressure of the gas in a rigid sealed container (N and V in the ideal gas law equation stay constant, just as in a can of spray paint).

The container was a glass flask, sealed with a rubber stopper.  A piece of tubing with a valve was connected to the flask.  The valve was opened at the start of the demonstration to be sure the pressures inside and outside the flask were equal.  The valve was then closed.  The manometer is a U-shaped tube filled with a liquid (transmission oil) that can detect differences in pressure.  Pressure from the air inside the flask could enter one end of the manometer tube.  The other end was exposed to the pressure of the air outside the flask. 

Green in the figure indicates that the temperatures of the air inside and outside the flask were equal.  The manometer is showing that the pressure of the air inside and outside the flask were equal.


I wrapped my hands around the flask to warm the air inside very slightly.  The increase in air temperature caused a slight increase in the pressure of the air inside the flask.  The air outside didn't change.  Note the change in the levels of the liquid in the manometer indicating the increase of the air pressure inside the flask.

The valve was opened momentarily so that the pressures inside and out would again be equal.  The valve was then closed and some isopropyl alcohol (rubbing alcohol) was dribbled on the outside of the flask.  As the alcohol evaporated it cooled the flask and the air inside the flask.  This caused the air pressure inside the flask to drop.  This change in air pressure was again indicated by the liquid levels in the manometer.

Volume
The effect of volume on pressure might be a little harder to understand.  Just barely fill a balloon with air, wrap your hands around it, and squeeze it.  It's hard to compress the balloon, you can't really compress it very much at all.


Think of the bottom layer of the atmosphere being squished by the weight of the air above.  As the bottom layer is compressed and its volume shrinks it pushes back with enough force to eventually support the air above.



A decrease in volume causes an increase in pressure, that's an inverse proportionality. 



It might take three or four breaths of air to fill a balloon.  Think about that.  You add some air (N increases) and the balloon starts to inflate (V increases).  Then you add another breath of air.  N increases some more and the balloon gets a little bigger, V has increased again.  As you fill a balloon N and V are both increasing.  What is happening in this case is that the pressure of the air in the balloon is staying constant.  The pressure inside the balloon pushing outward and trying to expand the balloon is staying equal to (in balance with) the pressure of the air outside pushing inward and trying to compress the balloon.

Here's the same picture again except N and V are decreasing together in a way that keeps pressure constant.  This is exactly what occurs during Experiment #1.

 
Experiment #1 - P stays constant, N & V both decrease

Here's a little more detailed explanation of Expt. #1



The object of Experiment #1 is to measure the percentage concentration of oxygen in the air.  An air sample is trapped together with some steel wool inside a graduated cylinder.  The cylinder is turned upside down and the open end is stuck into a glass of water sealing off the air sample from the rest of the atmosphere.  This is shown at left above.  The pressure of air outside the cylinder tries to push water into the cylinder, the pressure of the air inside keeps the water out.

Oxygen in the cylinder reacts with steel wool to form rust.  Oxygen is removed from the air sample which causes N (the total number of air molecules) to decrease.  Removal of oxygen would ordinarily cause a drop in Pin  and upset the balance between Pin  and Pout .  But, as oxygen is removed, water rises up into the cylinder decreasing the air sample volume.  The decrease in V is what keeps Pin  equal to Pout .  N and V both decrease together in the same relative amounts and the air sample pressure remains constant.  If you were to remove 20% of the air molecules, V would decrease to 20% of its original value and pressure would stay constant.  It is the change in V that you can see, measure, and use to determine the oxygen percentage concentration in air.  Those of you doing the experiment should try to explain this in your experiment report.

You might think that the mass of the gas molecules inside a balloon might affect the pressure (big atoms or molecules might hit the walls of the balloon harder and cause higher pressure and vice versa).


The mass of the air molecules doesn't matter.  The big ones move relatively slowly, the smaller ones more quickly.  They both hit the walls of the balloon with the same force.  A variable for mass doesn't appear in the ideal gas law equation.

The ideal gas law equations
The figure below shows two forms of the ideal gas law.  The top equation is the one we've been looking at and the bottom is a second slightly different version.  You can ignore the constants k and R if you are just trying to understand how a change in one of the variables would affect the pressure.  You only need the constants when you are doing a calculation involving numbers and units (which we won't be doing).



The ratio N/V is similar to density (mass/volume).  That's where the ρ (density)  term in the second equation comes from.

Step #2 (in our effort to understand why warm air rises and cold air sinks) Charles' Law


A volume of air in the atmosphere is not a rigid container.  Air is free to expand or shrink and will do so in order to keep the pressures inside and outside the volume in balance.  The figure above is on page 52 in the ClassNotes.

Charles Law refers to situations where P (pressure) in the ideal gas law stays constant.  Changing the temperature of a volume of air will cause a simultaneous change in density and volume; pressure will stay constant.  This is an important situation because this is how volumes of air in the atmosphere behave.

A series of pictures can help understand why and how this happens


We'll start out with a volume (a parcel) of air.  The temperature and density of the air inside and outside the volume are the same.  So the outward pressure produced by the air inside the volume is equal to and in balance with the inward pointing pressure produced by the air surrounding the balloon.

Next we'll warm up the air inside the volume.  The air outside the volume stays the same.






You can go through the same reasoning with a volume of air that cools.  In this case move from right to left to see the cooling and the changes that occur.


If you want to skip all the details and just remember one thing, here's what I'd recommend






Demonstration of Charles Law in action
Parcels of atmospheric air and air in balloons behave the same way, they both obey Charles' Law.  Charles Law can be demonstrated by dipping a balloon in liquid nitrogen.  You'll find an explanation on the top of page 54 in the ClassNotes.


A balloon shrinks down to practically zero volume when dunked in the liquid nitrogen.  When pulled from the liquid nitrogen the balloon is filled with very cold, very high density air. 

Then the balloon starts to warm up.




 The volume and temperature both increase together in a way that kept pressure constant (pressure inside the balloon is staying equal to the air pressure outside the balloon).  Eventually the balloon ends up back at room temperature (unless it pops while warming up).

Step #3 Two vertical forces acting on a parcel of air in the atmosphere

Let's start with a parcel of air that is neutrally buoyant.  I.e. it doesn't rise or sink, it hovers.


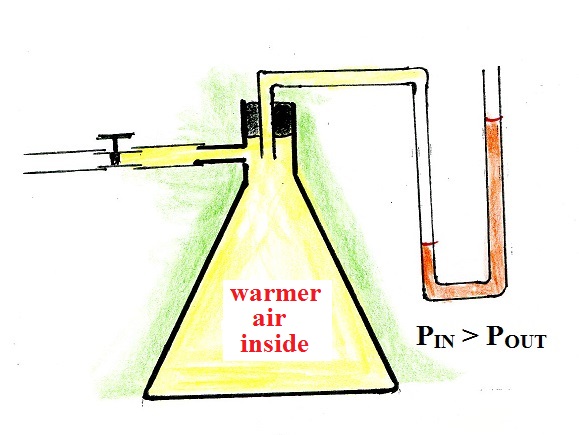
How is this possible?  We know that gravity exerts a downward force on the air parcel (shown in the left figure below).  What keeps it from sinking?  There must be an upward force of equal strength to cancel out the effect of gravity.










The upward force is produced by the air surrounding the parcel that pushes on the bottom, top, and sides of the volume of air.  Pressure decreases with increasing altitude.  So the pressure pushing upward at the bottom of the parcel is a little stronger than the pressure downward on the top of the balloon.  The overall effect is an upward pressure difference force. 




The strength of the upward pressure difference force depends on the distance between the top and bottom of the balloon. 

Now we will look at what happens if we warm or cool the volume of air.

When we warm the air parcel its volume will increase.  The density of the air inside the parcel will decrease but the parcel's weight stays the same; it still contains the same amount (mass) of air.  The pressure difference force has increased because the distance between the top and bottom of the parcel is larger.  The upward pressure difference force is now stronger than the downward gravity force (the weight).  The net force is upward and the parcel will rise.

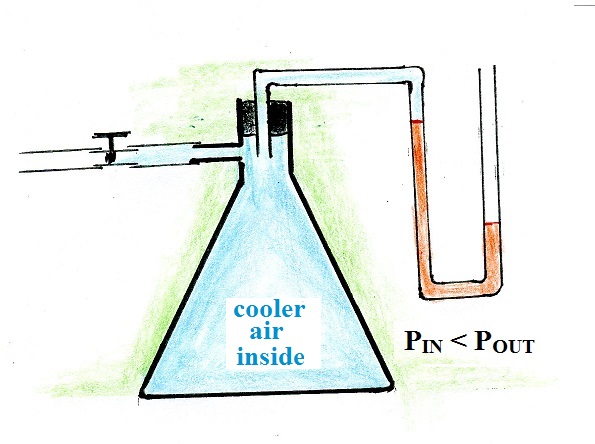
When you cool the air the volume shrinks.  The pressure difference force becomes weaker.  The volume still contains the same amount of air so its weight hasn't changed.  The downward force is now stronger than the upward force.  The net force is downward and the parcel will sink. 


Convection demonstration
Here's a short demonstration of the role that density plays in determining whether a balloon will rise or sink (or hover)





We used balloons filled with helium (see bottom of page54 in the photocopied Class Notes).  Helium is less dense than air even when it has the same temperature as the surrounding air.  The downward gravity force (weight of the helium filled balloon) is weaker than the upward pressure difference force.  You don't need to warm a helium-filled balloon to make it rise.







We dunk the helium filled balloon in liquid nitrogen to cool it off.  When you pull the balloon out of the liquid nitrogen it has shrunk.  The helium is denser than the surrounding air.  I set it on the table (dark blue above) and it just sat there.

As the balloon of helium warms and expands its density decreases (light blue).  For a brief moment it has the same density as the surrounding air (green).  It's neutrally buoyant at this point, it would hover.  Then it warms back to near room temperature where it is again finds itself less dense than the air and lifts off the table (yellow).
Free convection
Free convection is one way of causing rising air motions in the atmosphere.  We will soon see that rising air is important because it can lead to cloud and storm formation.



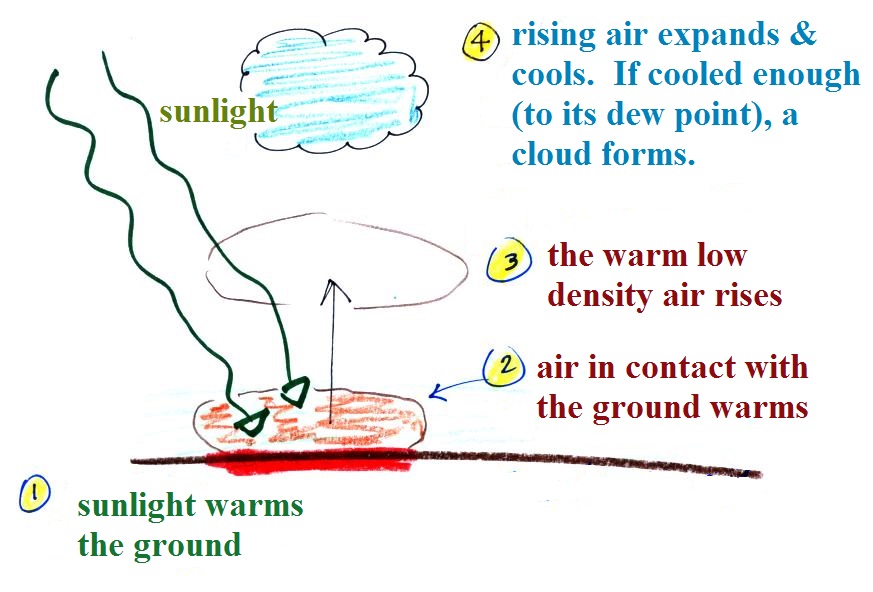
Sunlight shines through the atmosphere.  Once it reaches the ground at (1) it is absorbed and warms the ground.  This in turns warms air in contact with the ground (2)  As this air warms, its expands and its density starts to decrease (pressure is staying constant).  When the density of the warm air is low enough (lower than the surrounding air), small "blobs" of air separate from the air layer at the ground and begin to rise, these are called "thermals."  (3) Rising air expands and cools (we've haven't covered this yet and it might sound a little contradictory).  If it cools enough (to the dew point) a cloud will become visible as shown at Point 4.  This whole process is called convection; many of our summer thunderstorms start this way.


Archimedes' principle
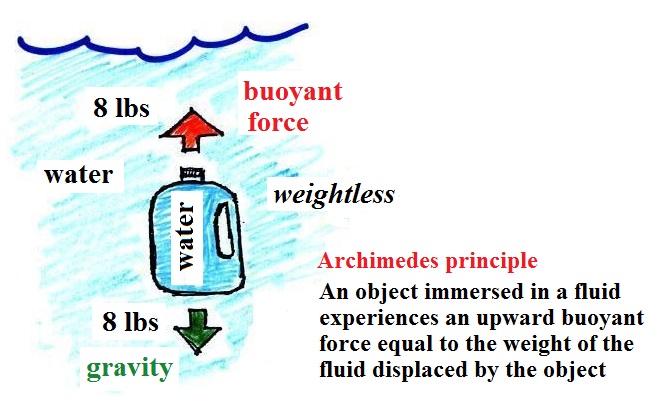
Here's another way of trying to understand why warm air rises and cold air sinks - Archimedes Law or Principle (see page 54a & page 54b in the ClassNotes).  It's perhaps a simpler way of understanding the topic.  A gallon bottle of water can help you to visualize the law.



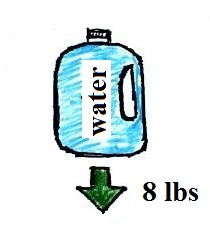
A gallon of water weighs about 8 pounds (lbs).  I wouldn't want to carry that much water on a hike unless I thought I would really need it.

Here's something that is kind of surprising.
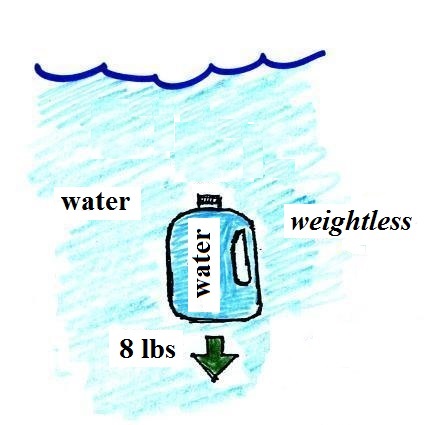
If  you submerge the gallon of water in a swimming pool, the jug becomes, for all intents and purposes, weightless.  The weight of the water (the downward gravity force) doesn't just go away.  Once the jug is immersed, there must be an upward force of some kind, one that can cancel out gravity.  Archimedes' recognized that this would happen and was able to determine how strong the upward force would be.


The strength of the upward buoyant force is the weight of the fluid displaced by the bottle.  In this case the 1 gallon bottle will displace 1 gallon of pool water.  One gallon of pool water weighs 8 pounds.  The upward buoyant force will be 8 pounds, the same as the downward force.  The two forces are equal and opposite.

What Archimedes law doesn't really tell you is what causes the upward buoyant force.  You should know what the force is - it's the upward pressure difference force.





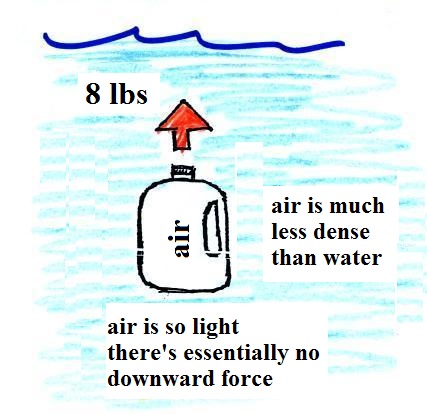
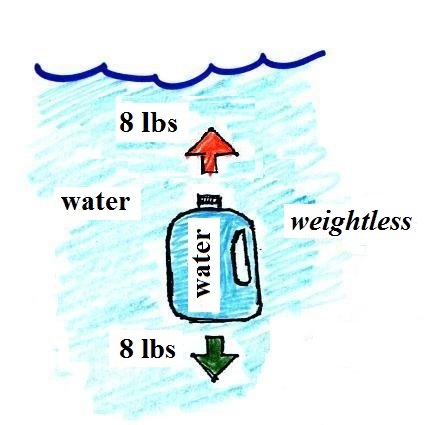
We've poured out the water and filled the 1 gallon jug with air.  Air is much less dense than water; compared to water,  the jug will weigh practically nothing.  But it still displaces a gallon of water and experiences the 8 lb. upward buoyant force.  The bottle of air would rise (actually it shoots) up to the top of the pool. The density of the material inside and outside the bottle are the same. A bottle filled with water is weightless. 

Next we'll fill the bottle with something denser than water (I wish I had a gallon of mercury)
Sand is about 50% denser than water.  The weight of a gallon of sand is more than a gallon of water.  The downward force is greater than the upward force and the bottle of sand sinks.


You can sum all of this up by saying anything that is less dense than water will float in water, anything that is more dense than water will sink in water.


Most types of wood will float (ebony and ironwood will sink).  Most rocks sink (pumice is an exception).

The fluid an object is immersed in doesn't have to be water, or even a liquid for that matter.  You could immerse an object in air.  So we can apply Archimedes Law to parcels of atmospheric air. 



Air that is less dense (warmer) than the air around it will rise.  Air that is more dense (colder) than the air around it will sink.

Here's a little more information about Archimedes.

End of Quiz #1 Material.
This section on the Galileo thermometer is interesting, but will not be covered on any quiz or exam this semester.
I want to show one last application of some of what we have been learning - a Galileo thermometer.  That's assuming it survives the trip from my office to our classroom.  It's fairly fragile. 






The left figure above comes from an interesting and informative article in Wikipedia.  The right figure is a closeup view of the thermometer I brought to class.
Here's an explanation of how/why a Galileo thermometer works.  It requires some time to process.

Just like air, the fluid in the thermometer will expand slightly if it warms.  It will shrink when it cools.



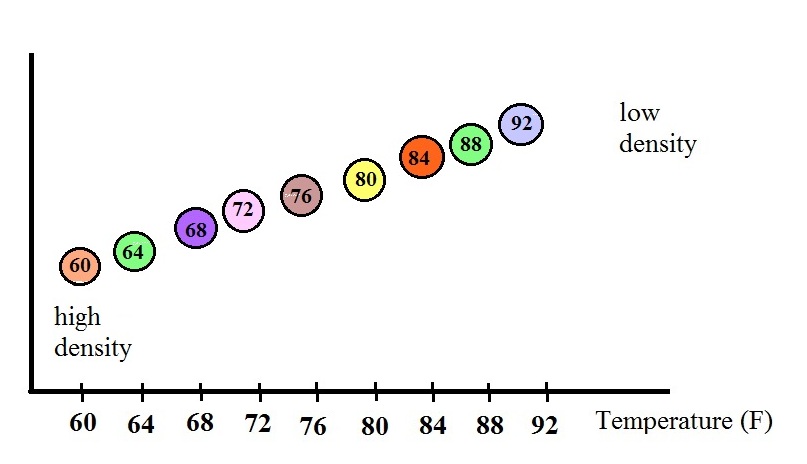
The changes in the volume of the fluid will change the fluid's density.  The graph above shows how the fluid density might change depending on temperature.  Note lower densities are found near the top of the graph (the fluid expands as it warms).


The colored balls in the thermometer all have slightly different densities.  They also all have little temperature tags.  The 60 F ball has a density equal to the density of  the fluid at 60 F.  The 64 F ball has a slightly lower density, the density of the fluid when it has warmed to 64 , and so on.  The densities of the floats don't change.






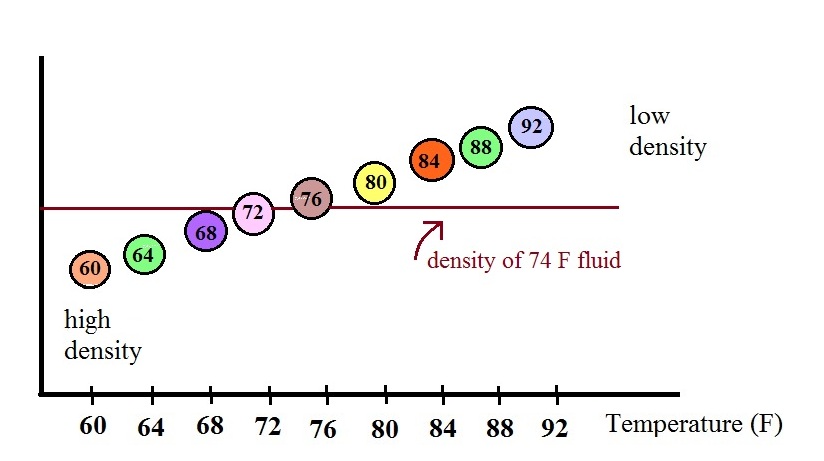
In use the density of the fluid in the thermometer will change depending on the temperature.  The densities of the balls remain constant.  As an example we will that the fluid in the thermometer has a temperature of 74 F.  The 60, 64, 68, and 72 F balls will all have densities higher than the fluid (they lie below the 74F line in the graph above) and will sink.  The remaining balls have densities lower than the fluid and will float.

The lower most floating ball in the illustration has a 76 F temperature tag.  The uppermost of the balls that have sunk reads 72 F.  The temperature is something between 72 F and 76 F.  With this thermometer you can only determine temperature to the nearest 4 F.  Also the thermometer takes quite a while to respond to a change in temperature (may be an hour or two.