Tuesday, Nov. 12, 2019
Flor de Toloache: "Meet the
all-female band redefining mariachi, Flor de Toloache"
(4:14), "Dulces
Recuerdos" (3:37), "Long Gone
Girl" (3:13), "Haupango
Melody" (6:54), "Besos de
Mezcal" (3:08), "Dicen"
(4:21)
I'm going to print page 121, page 122a, page 122b, page 122c, page 123a, page 123b, page 124a, page 125, page 126, page 127, page 128, page 129, and page 130. What we
don't use today we'll use on Thursday.
How and why surface and upper level winds blow the way
they do.
Some real world examples are shown in the figure below (found
on page 121 in the ClassNotes). The two largest types of
storm systems, middle latitude storms (extratropical cyclones) and
hurricanes (tropical cyclones), develop around surface centers of
low pressure
the term cyclone
refers to winds blowing around a center of low pressure
Earlier in the semester we learned that winds spin
counterclockwise around centers of low pressure in the northern
hemisphere. Today we start to worry about what happens in
the southern hemisphere. Winds change direction and spin
clockwise around low pressure in the southern hemisphere.
Winds spin clockwise around "anticyclones" (high pressure) in the
northern hemisphere and counterclockwise around highs in the
southern hemisphere.
Why do winds blow in opposite
directions around high and low pressure? Why do they
even spin at all?
Why do the winds change directions when you move from the
northern to the southern hemisphere?
These are the kinds of questions we'll be addressing.
And it's not just the wind. Ocean currents off the East
and West Coasts of the US spin in a clockwise direction.
They reverse direction and spin counterclockwise off the east and
west coasts of South America.
Something else to notice in the figure. Storm systems
in the tropics (0 to 30 degrees latitude) generally move from
east to west in both hemispheres. At middle latitudes
(30 to 60 degrees), storms move in the other direction, from
west to east. That's not something we will cover in
class, rather that will be the subject of the upcoming Thermal
Circulation/3-cell model assignment (you'll have the option of
earning either 1S1P or Extra Credit points).
We'll be able to learn most of what we need to know about
surface and upper level winds in 10 relatively easy steps (though
I've broken several of the steps into smaller parts).
At some point I'll also probably lose track of exactly what
step we're working on.
Step #1 - Upper level and surface winds in the N. and
S. hemisphere - summary
This is an important figure (page 122a in the ClassNotes)
because it summarizes much of what we are about to learn.
Upper level winds are shown in the first set of four pictures
above. All the possibilities (H and L pressure in both the
northern and southern hemispheres) are here. The first thing
to notice is that upper level winds blow parallel to the
contours. Just 2 forces, the pressure gradient force (PGF) and the Coriolis force (CF), cause the winds to blow this
way. Eventually you should be able to draw the directions of
the forces for each of the four upper level winds examples.
Here is an
upper level wind example showing what you should be able to
do.
The four drawings at the bottom of the page show surface winds
blowing around high and low pressure in the southern
hemisphere. Surface winds blow across the contour lines
slightly, always toward low pressure. A third force,
the frictional force is what causes this to occur. He
is an example of
what you will be able to say about surface winds.
Step #2 - Newton's 1st law of motion
The next few figures are on page 122b in the ClassNotes.
We start with a statement of Newton's 1st law of motion.
If there's no net force being exerted on an object it will
either be stationary or moving in a straight line at constant
speed.
Anytime an object is slowing or speeding up or changing direction
(or both) a net force is present.
You should be able to look at an object's (or the wind's)
motion and tell if there is a net force or not. There are
two possibilities where there is no net force. The
first is shown below.
The two objects above are stationary. In both cases there
is no net force. That could mean there aren't any forces
at all (left figure). Or forces may be present but they
cancel each other out and add up to zero (the total force is
zero). With zero net force both objects will remain
stationary.
The other possibility is that something is moving in a
straight line at constant speed.
As long as the net force remains zero both objects will
continue to move in a straight line at constant speed.
Note in the bottom figure the two forces could have been
pointing right and left . If they cancel each other
out the total force is zero and the object would continue to
move in a straight line at constant speed.
Here are some more examples of straight line motion.
The speed is also constant in examples (a)
and (f) so there is no net force in those two cases
only.
The speed is changing in (b), (c), (d), and (e). A net
force is present and you should be able to determine its
direction. Maybe you can figure that out just by
looking at the pictures, maybe not (sometimes it helps to
turn the picture 90 degrees so the motion is horizontal not
vertical). What you might do is think of a situation
you're familiar with.
Here's a picture of someone
throwing a ball upward. You know from personal
experience that the downward force of gravity will cause
the ball to slow down as it rises, come to a stop, and
then begin to fall picking up speed as it falls.
Gravity is present during both the rise and fall of
the object.
We can match up the motion and force arrows with (b)
and (e) in the earlier example.
Notice how the motion in (b) resembles that of a falling
ball. The motion in (e) is just like the motion of the
ball thrown upward in the air. Notice also
that when the force is pointing in the same direction as the
motion the object speeds up. The object slows down when
the force arrow points opposite the motion. Now you can
figure out the direction of the forces in (c) and (d).
The next figure shows a more important example - circular
motion. Is there a net force in any of
these examples? The answer is yes, a net force is present
in all three cases because the motion is not straight line
motion at constant speed. What is the direction of the net
force?
My sister can help with this question
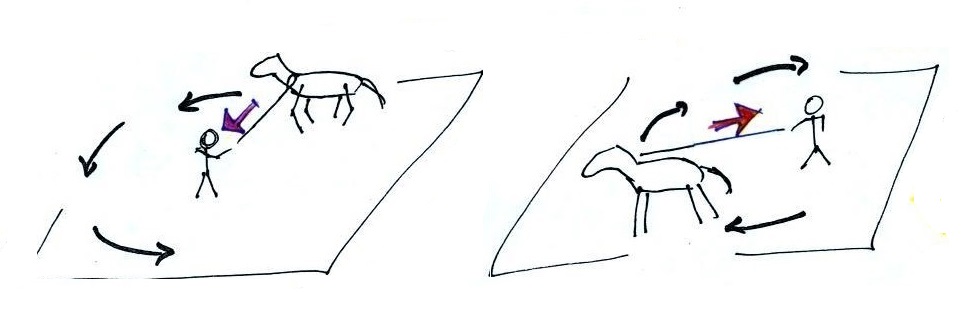
She's out longeing
(it doesn't look right, but I believe that is the correct
spelling) one of her horses, training it to run in a circle
and to obey her commands. At least initially the horse
doesn't really want to do that and you must pull with a lot
of force to keep it moving in a circle (without a force it
would move in a straight line). It's relatively easy
to understand when you imagine a strong heavy horse at the
end of a longe line that a net inward force is needed
anytime anything moves in a circular path.

It doesn't matter what the direction of spin is, it doesn't
matter what's in the middle of the picture; anytime
something is moving in a circle there is a net inward force
(gravity is the inward force keeping the satellite in orbit
in the 3rd picture).
Here's a question I know many people will have
trouble with (but better to have trouble here in the online
notes rather than in the middle of a quiz). Keeping
an image of a horse on the end of a longe line might help.

Is there a net inward or outward
force in each case? You should now know that there is a
net inward force in the 1st example because that's what we
just looked at. What about the next two. The 3rd
example is the one that causes people the most trouble.
Here's a clue >>> Goldilocks and the Three
Bears. The clue will make more sense when you look at
the answer to this question at the end of today's notes.
Now
we'll start to look at the forces
that cause the wind to blow.
Step #3
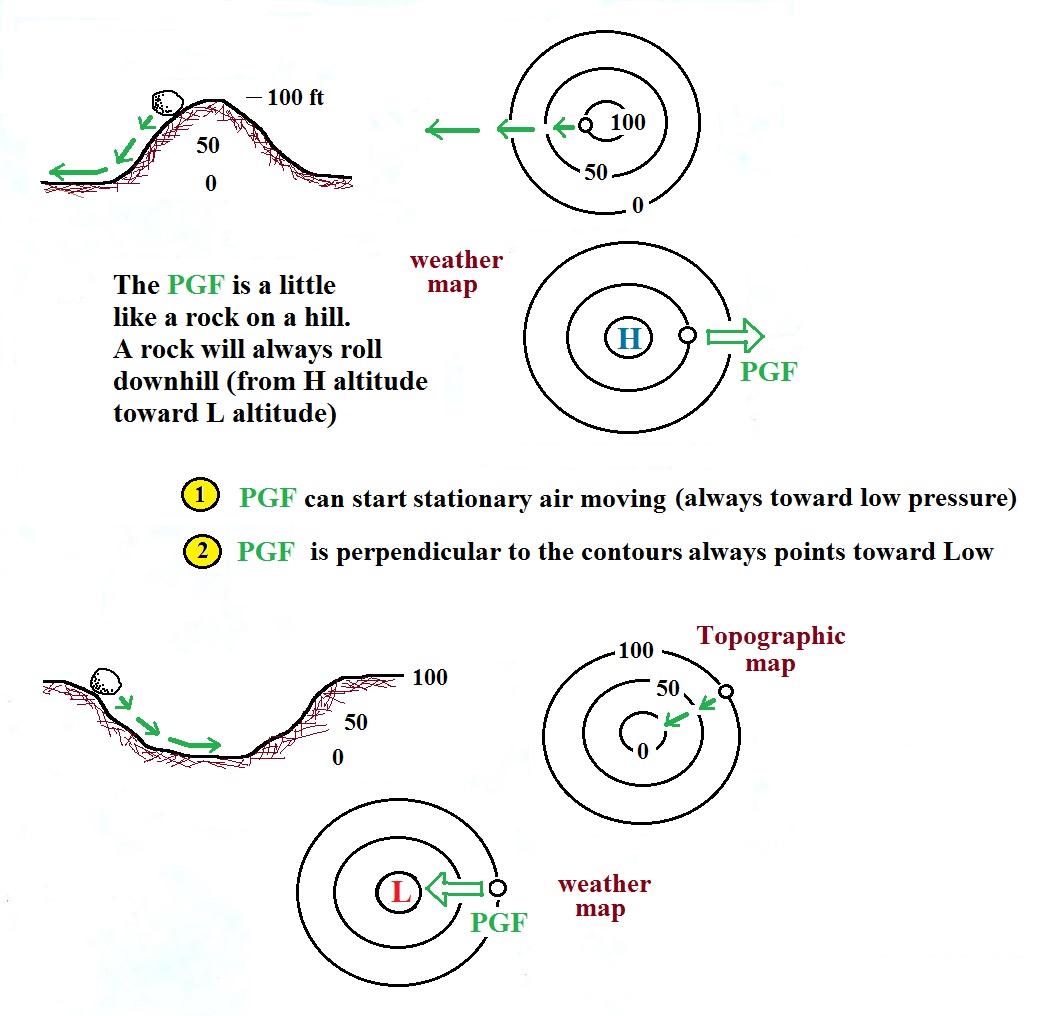
Pressure Gradient Force (PGF)
The figure below is on page 123a
in the ClassNotes)
Isobars on a weather map are very much like height contours on a
topographic map. A center of low pressure on a weather map
is analogous to a circular valley on a topographic map (high
pressure on a weather chart is like a circular hill).
The
effect that the PGF force
has on air
is very much like the effect of gravity on a
rock placed on a slope.
The rock will roll downhill, air will move
toward low pressure.
The PGF always points in a direction that is perpendicular to the
contour lines and toward low pressure. The PGF can start
stationary air moving. The air will always start moving
toward low pressure. Air moving inward toward low pressure
or outward away from high pressure is similar to a rock rolling
downhill into the center of a depression or downhill and outward
away from the summit of a hill.
It's good to understand the pressure gradient force as
best you can. But at the same time it's nice to have
some rules that you can fall back on and apply. The
rules for the PGF are shown above. Follow them
(especially the one for direction) to the letter and
you'll never go wrong.
Use the following figure to test yourself. With an
arrow draw the direction of the PGF at each of the points
in the figure. You'll find the answers at the end of
today's notes.
Step #4 - Coriolis force (CF)
In this case we'll start with the rules and put some
discussion of what causes this force into some online
Optional Reading. The rules for the CF are
shown below.
The top of page 123b in the ClassNotes has several examples
showing the direction of the CF. You can use them to check
and make sure you understand how to apply the direction rule
above. I would suggest
turning the page in your class notes so that you are
looking in the direction the wind is blowing, looking
downstream, whenever you try to
determine the direction of the Coriolis force.
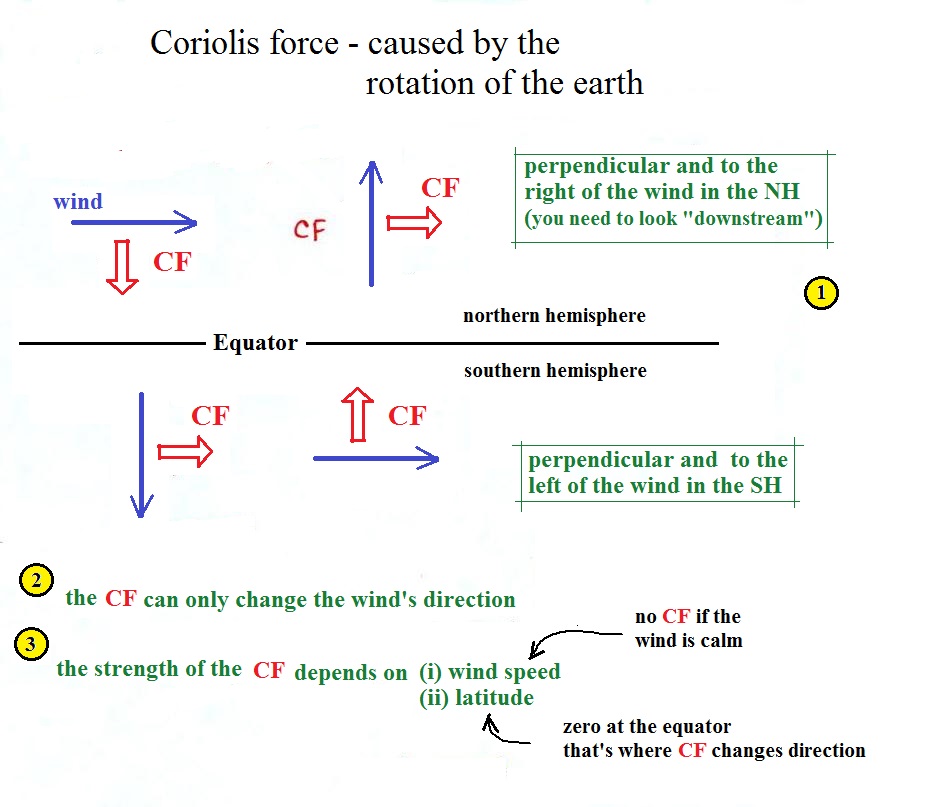
The Coriolis force is caused by the rotation of the earth.
Again you can read more
online. The CF points perpendicular to the wind and
is to the right or left depending on hemisphere. Be sure
you are looking in the direction the wind is blowing, looking
downstream, when determining the direction of the CF.
The CF can only change the wind's direction. It can't
cause the wind to speed up or slow down.
There isn't any Coriolis force when the wind is calm.
Coriolis force is zero at the equation because that's where the
CF changes direction. Hurricanes don't form at the equator
because there is no Coriolis force there.
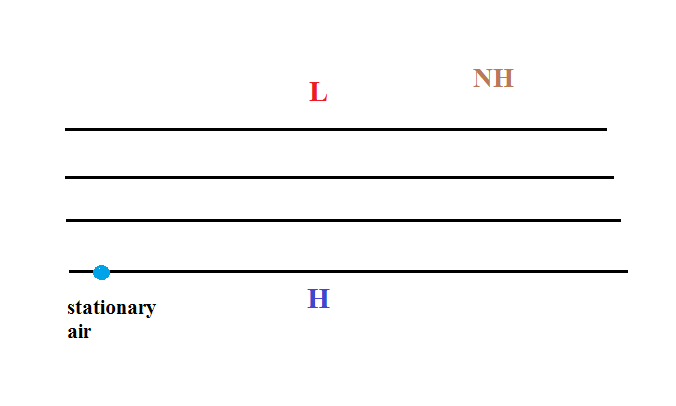
Time now to begin to apply what we've
learned so far. See page 124a in the ClassNotes
We'll consider the simplest possible situation - upper
level winds with straight contours. We'll do a
Northern Hemisphere (NH) example.
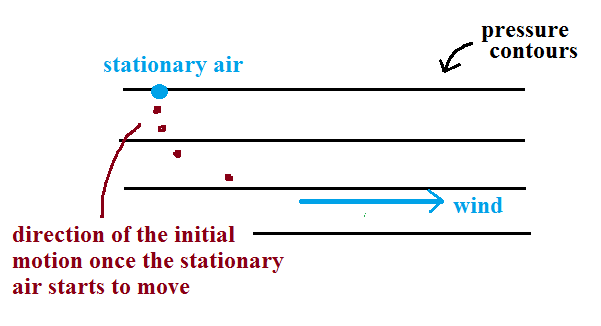
We start with some stationary air in
the lower left corner of the picture. Low pressure
is at the top and high pressure at the bottom of the
picture.
The PGF can start stationary air moving. The PGF
will point toward the top of the picture (perpendicular to
the contours and toward the low pressure at the
top). There won't be any Coriolis force when the air
is stationary.
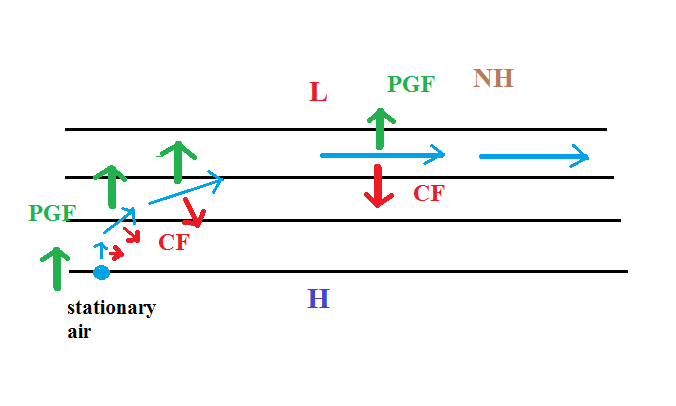
Once the wind starts to blow (blue line
above) the CF will appear. The CF will be weak at
first because the wind speed is low but the CF will begin
to turn the wind to the right. As the wind picks up
speed the CF will increase in strength. Eventually
the wind will be blowing parallel to the contours from
left to right. The PGF and CF point in opposite
directions and are of equal strength. The net
force is now zero and the wind will continue to blow to
the right in a straight line at constant speed.
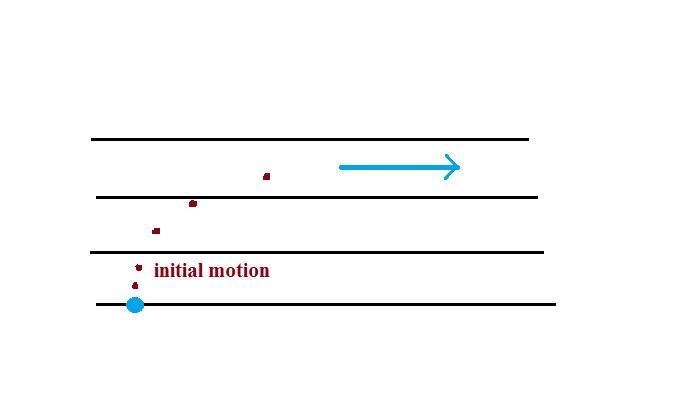
Here's a simpler less cluttered way of depicting what we
have just figured out.
The
dots show the direction of the initial
motion. That will always
be toward low pressure. Then
you look in the direction the wind starts
to blow and look to see if the wind turns
right or left. It turned right in
this case. That's the effect of the
Coriolis force and means this is a
northern hemisphere map.
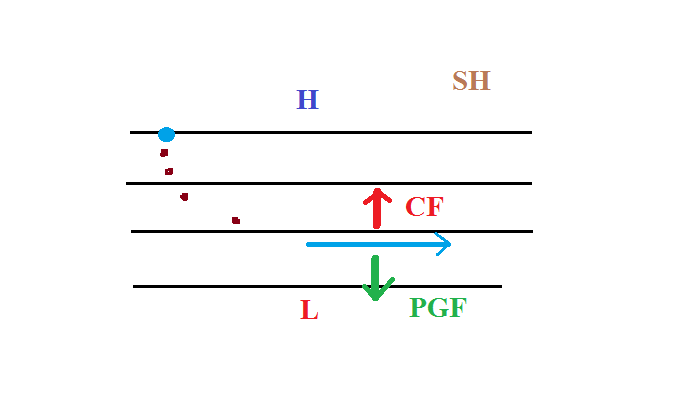
Here's one last example to test your
understanding.
The direction
of the initial motion is shown with dots.
Where is the high and low pressure in this
case? Is this a NH or SH chart? You'll
find the completed map at the end of today's
notes.
Step #5 - Upper level winds, low
pressure, northern hemisphere
Next we'll be looking at the upper level winds that develop around
circular centers of high and low pressure.
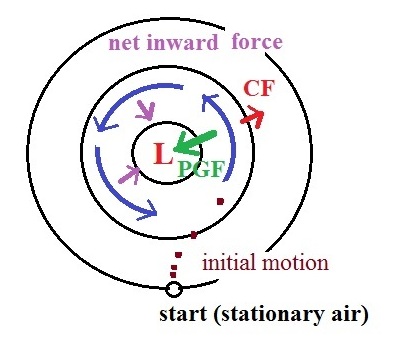
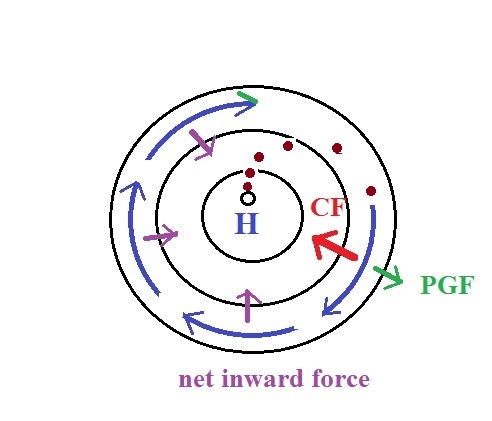
We start with some stationary air at the bottom of the
picture. Because the air is stationary, there is no
Coriolis force. There is a PGF force,
however. The PGF at
Point 1 starts stationary air moving toward the center of low
pressure (just like a rock would start to roll downhill).
The dots show the initial motion
A rock would roll right into the center of the picture.
Once air starts to move, the CF
causes it to turn to the right (because this is a northern
hemisphere chart). As the wind speeds up the CF strengthens. The wind
eventually ends up blowing parallel to the contour lines and
spinning in a counterclockwise direction. Note that the
inward PGF is stronger than
the outward CF. This
results in a net inward force,
something that is needed anytime wind blows in a circular path.
Upper level winds spin counterclockwise around low pressure
in the northern hemisphere.
Step #6 - Upper level winds, low pressure, southern
hemisphere
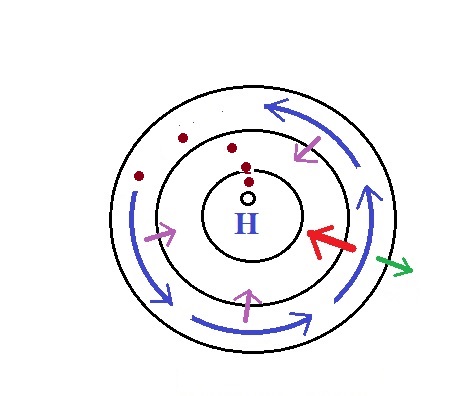
We start again with some stationary air at Point 1 in this
figure. The situation is very similar. Air starts to
move toward the center of the picture but then takes a left hand
turn (the CF is to the left
of the wind in the southern hemisphere). The winds end up
spinning in a clockwise direction around low in the southern
hemisphere. The directions of the PGF, CF,
and the net inward force
are all shown in the picture.
Upper level winds spin clockwise around low pressure in the
southern hemisphere.
Step #7 - Upper level winds, high pressure, northern
hemisphere
Here initially stationary air near the center of the picture
begins to move outward in response to an outward pointing
pressure gradient force (PGF
is pointing toward low pressure which is on the edges of the
picture). Once the air starts to move, the Coriolis force
(CF) will cause the wind to
turn to the right. The dots show the initial outward
motion and the turn to the right. The wind ends up blowing
in a clockwise direction around the high. The inward
pointing CF is stronger
than the PGF so there is a
net inward force here just
as there was with the two previous examples involving low
pressure. An inward force is needed with high pressure
centers as well as with centers of low pressure. An inward
force is needed anytime something moves in a circular path.
Step #8 - Upper level winds, high pressure, southern
hemisphere
This is a southern hemisphere upper level center of high
pressure. The air starts to move outward again but
this time takes a left hand turn and ends up spinning
counterclockwise. The net force is inward again.
I'm guessing that we'll be about out of
time at this point, so I've moved Steps #9 and #10 to the
start of the Thursday, Nov.
14 notes.
Here are the answers to the two questions embedded in today's
notes.
A net inward force is needed in all three cases.
The thing that changes is the strength of the inward
force.
This figure shows the directions of the PGF at each of the
highlighted points. The mistake many people make
is to draw the arrow pointing straight toward the L. But the PGF arrow
must also always be perpendicular to the contour lines.
The initial motion is always toward L pressure which must be at
the bottom of this map. Then if you turn the map so that you
can look downstream in the direction of the initial motion you'll
notice the wind turning to the left indicating this is a
southern hemisphere map.